
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекція 10
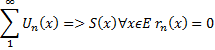
§1 Критерій Коші збіжності функціональних рядів. Достатня ознака рівномірної збіжності функціональних рядів
Критерій Коші:
Для того, щоб функціональний ряд
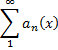
Був рівномірно збіжним в області збіжності необхідно і досить, щоб 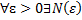 не залежить від х:
не залежить від х: 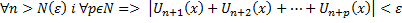
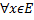 .
.
Теорема Вейєрштрасса (достатня умова):
Якщо для функціонального ряду 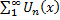 з неперервними на [a, b] членами ряду існує такий числовий ряд
з неперервними на [a, b] членами ряду існує такий числовий ряд 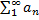 - збіжний, де
- збіжний, де 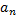 > 0 такий, що
> 0 такий, що 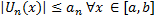 , то даний ряд рівномірно збіжний для будь якого х з проміжку [a, b].
, то даний ряд рівномірно збіжний для будь якого х з проміжку [a, b].
Доведення:
Збіжність ряду 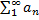 за критерієм Коші збіжний числовий ряд, що
за критерієм Коші збіжний числовий ряд, що 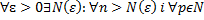 виконується
виконується 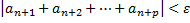 . Розглянемо
. Розглянемо 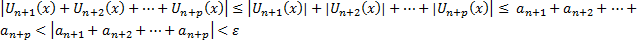
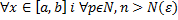
Висновок: за критерієм Коші функціональний ряд збіжний.
§2 Властивості рівномірно збіжних функціональних рядів
Теорема 1 (про неперервність суми рівномірно збіжного функціонального ряду)
Якщо члени ряду:
1. Неперервні на [a, b]
2. Ряд рівномірно збіжний на [a, b], то його сума S(x) є неперервною функцією на [a, b]
Доведення:
Неперервність членів ряду забезпечує неперервність його частинних сум 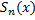 . Тобто
. Тобто 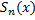 неперервні в
неперервні в 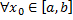 , це означає, що
, це означає, що 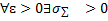 :
: 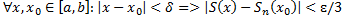
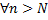
Розглянемо різницю між 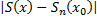 за умов (2) ми маємо
за умов (2) ми маємо 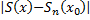 => x
=> x 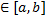
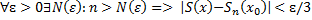
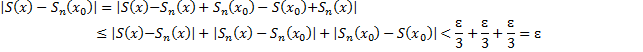
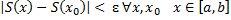
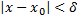
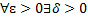 => S(x) неперервна на [a, b]
=> S(x) неперервна на [a, b]
Приклад:
1. (1-x)+(x- 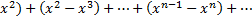
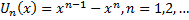
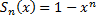
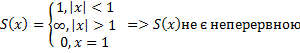
Зауваження: 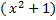
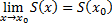
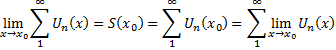
В рівномірно збіжному функціональному ряді почленно можна переходити до границі.
2. 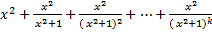
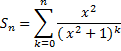
Геометрична прогресія, b= 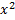 , q=
, q= 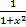
S= 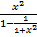 =
= 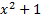
S(0)=0; 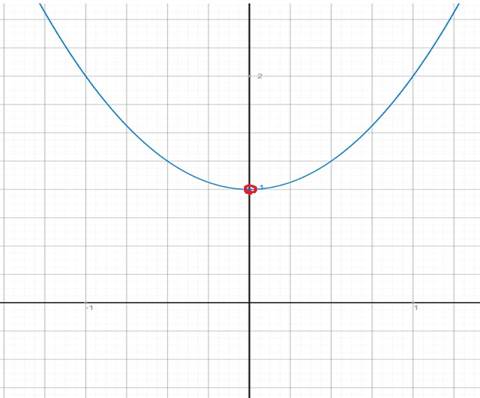
3. Дано функціональний ряд 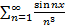 . Дослідити на рівномірну збіжність.
. Дослідити на рівномірну збіжність.
Означення:
Числовий ряд
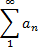
Такий, що для членів
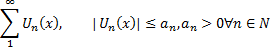
Називається мажорантою функціонального ряду. Тоді 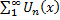 - міноранта.
- міноранта.
Отже, 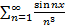 збігається рівномірно на R.
збігається рівномірно на R.
Теорема 2 (про інтегрованість рівномірно збіжного функціонального ряду)
Якщо члени функціонального ряду
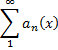
1) Неперервні на [a, b]
2) Ряд рівномірно збіжний на [a, b]
То його можна почленно інтегрувати на 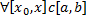 одержимо ряд:
одержимо ряд:
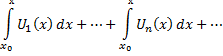
Одержаний ряд рівномірно збіжний і його сума дорівнює інтегралу від суми даного ряду.
Теорема стверджує, що рівномірно збіжний функціональний ряд можна почленно інтегрувати в області збіжності.
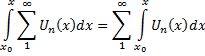
Приклад:
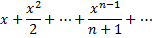
G(x)=? Через 1+х+ 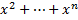
G(x)= 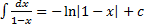
G(0)=0
0=-ln1+c => c=0
G(x)=-ln(1-x)
Теорема 3(про диференційованість рівномірно збіжного функціонального ряду)
Якщо члени: 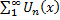
1) Неперервно диференційовані на [a, b]
2) Функціональний ряд 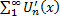 , одержаний із даного, шляхом диференціювання його членів, рівномірно збіжний на [a, b]
, одержаний із даного, шляхом диференціювання його членів, рівномірно збіжний на [a, b]
3) Даний ряд збігається 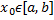
Тоді даний ряд можна почленно диференціювати. Сума одержаного ряду 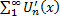 дорівнює похідній від суми даного ряду для х
дорівнює похідній від суми даного ряду для х 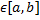 і даний ряд буде рівномірно збіжним.
і даний ряд буде рівномірно збіжним.
S(x)= 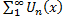
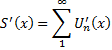
Приклад: 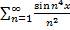
1. Неперервно диференційований на R
2. X=0 => ряд збіжний
3. Формально диференційований
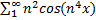 – розбіжний, диференціювання ряду неможливе
– розбіжний, диференціювання ряду неможливе
§3 Степеневі ряди. Теорема Абеля.
Означення:
Функціональний ряд виду 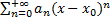
Називається степеневим рядом з центром розкладу в точці 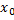 .
. 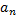 - коефіцієнт ряду
- коефіцієнт ряду
Розглядаємо ряд: 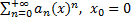
Теорема Абеля. Якщо степеневий ряд збігається при х= 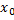 , то він абсолютно і рівномірно збіжний при таких х, що
, то він абсолютно і рівномірно збіжний при таких х, що 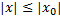 , якщо в точці
, якщо в точці 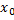 степеневий ряд розбігається, то він розбігається для всіх
степеневий ряд розбігається, то він розбігається для всіх 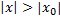
Означення:
Область збіжності степеневого ряду є інтервалом з центром в точці 0 (-R; R), поза яким степеневий ряд розбіжний. R – радіус збіжності степеневого ряду.
Для доведення теореми Абеля запишемо ряд у вигляді 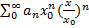
При х= 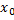 , степеневий ряд збіжний
, степеневий ряд збіжний
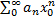 - збіжний =>
- збіжний => 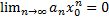 , кожне
, кожне 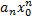 - обмежений числовий ряд, тобто існує M> 0:
- обмежений числовий ряд, тобто існує M> 0: 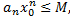 тоді
тоді
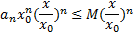
1) Тоді 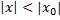 ,
, 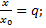 |q|< 1
|q|< 1
Отже 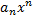 існує збіжна мажоранта
існує збіжна мажоранта 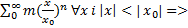 коли ряд збігається і рівномірно і абсолютно.
коли ряд збігається і рівномірно і абсолютно.
2)Якщо в точці 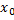 ряд розбігається, то
ряд розбігається, то 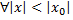 він розбіжний. Доведення від супротивного.
він розбіжний. Доведення від супротивного.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|