ЛЕКЦИЯ №10. Тема 9.1. Числовые ряды. Основные понятия: 1) Понятие числового ряда, его n-ый член и частичная сумма. 2) Сходящиеся и расходящиеся числовые ряды. 3) Сходимость и сумма ряда. 4) Необходимый признак сходимости ряда. Следствие. 5) Действия с ряд

РЯДЫ

ЛЕКЦИЯ №10

Тема 9. 1. Числовые ряды. Основные понятия: 1) Понятие числового ряда, его n-ый член и частичная сумма. 2) Сходящиеся и расходящиеся числовые ряды. 3) Сходимость и сумма ряда. 4) Необходимый признак сходимости ряда. Следствие. 5) Действия с рядами. 6) Исследование ряда геометрической прогрессии. 7) Исследование гармонического ряда.

Числовые ряды. Сходимость и сумма ряда

Бесконечные ряды широко используются в теоретических исследованиях математического анализа, имеют разнообразные практические применения.

Def: Числовым рядом (или просто рядом) называется выражение вида

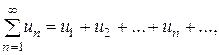(1)

где, 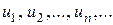– действительные или комплексные числа, называемые членами ряда, 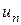– общий член ряда.

Ряд (1) считается заданным, если известен общий член ряда 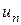, выраженный как функция его номера n: .

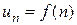Def: Сумма первых n членов ряда (1) называется n-й частичной суммой ряда и обозначается через 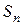, т. е. .

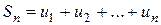Рассмотрим частичные суммы

, ,

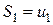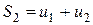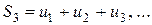
Def: Если существует конечный предел 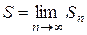последовательности частичных сумм ряда (1), то этот предел называют суммой ряда (1) и говорят, что ряд сходится.

Записывают .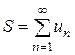

Если 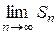не существует или 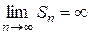, то ряд (1) называют расходящимся. Такой ряд суммы не имеет.

Рассмотрим примеры.

1. Ряд 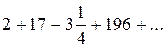нельзя считать заданным, а ряд 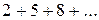– можно: его общий член задается формулой .

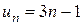2. Ряд 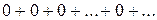сходится, его сумма равна 0.

3. Ряд 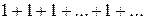расходится, 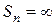при .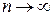

4. Ряд 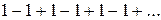расходится, так как последовательность частных сумм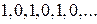 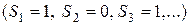не имеет предела.

5. Ряд 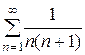сходится. Действительно,

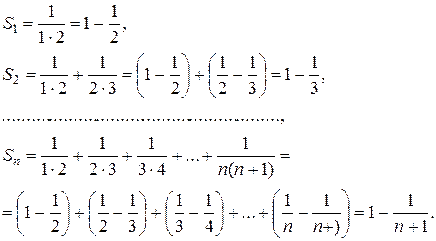
Следовательно,

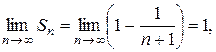
т. е. ряд сходится, его сумма равна 1.

Действия с рядами

Рассмотрим некоторые важные свойства рядов на основании которых выполняются действия с рядами.

Свойство 1. Если ряд (1) сходится и его сумма равна S, то ряд

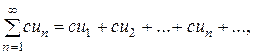(2)

где с – произвольное число, также сходится и его сумма равна сS. Если же ряд (1) расходится и с ¹ 0, то ряд (2) расходится.

Доказательство: Обозначим n-ю частичную сумму ряда (2) через 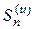. Тогда

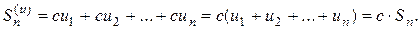
Следовательно,

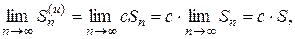
т. е. ряд (2) сходится и имеет сумму сS.

Покажем теперь, что если ряд (1) расходится, с ¹ 0, то и ряд (2) расходится. Допустим противное: ряд (2) сходится и имеет сумму S₁. Тогда

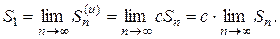
Отсюда получаем:

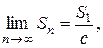
т. е. ряд (1) сходится, что противоречит условию о расходимости ряда (1).

Свойство доказано.

Свойство 2. Если сходится ряд (1) и сходится ряд

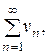(3)

а их суммы равны S₁ и S₂ соответственно, то сходятся и ряды

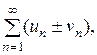(4)

причем сумма каждого равна соответственно .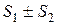

Доказательство: Обозначим n-е частичные суммы рядов (1), (3) и (4) через 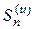, 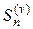и 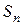. Тогда

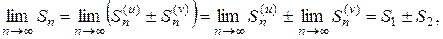
т. е. каждый из рядов (4) сходится, и сумма его равна 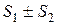соответственно.

Свойство доказано.

Из свойства 2 вытекает, что сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд.

В справедливости этого утверждения можно убедиться методом «от противного».

Заметим, что сумма (разность) двух расходящихся рядов может быть как сходящимся, так и расходящимся рядом.

Свойство 3. Если к ряду (1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (1) сходятся или расходятся одновременно.

Доказательство: Обозначим через S сумму отброшенных членов, через k – наибольший из номеров этих членов. Чтобы не менять нумерацию оставшихся членов ряда (1), будем считать, что на месте отброшенных членов поставили нули. Тогда при n > k будет выполняться равенство 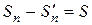, где 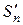– это n-я частичная сумма ряда, полученного из ряда (1) путем отбрасывания конечного числа членов. Поэтому 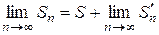. Отсюда следует, что пределы в левой и правой частях одновременно существуют или не существуют, т. е. ряд (1) сходится (расходится) тогда и только тогда, когда сходятся (расходятся) ряды без конечного числа его членов.

Свойство доказано.

Аналогично рассуждаем в случае приписывания к ряду конечного числа членов.

Ряд

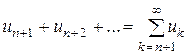(5)

называется n-м остатком ряда (1). Он получается из ряда (1) отбрасываем n первых его членов. Ряд (1) получается из остатка добавлением конечного числа членов. Поэтому, согласно свойству 3, ряд (1) и его остаток (5) одновременно сходятся или расходятся.

Из свойства 3 также следует, что если ряд (1) сходится, то его остаток 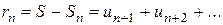стремится к нулю при 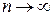, т. е. .

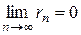Для исследования рядов на сходимость, в некоторых случаях, удобно пользоваться так называемыми эталонными рядами, являющимися рядами с положительными членами. К эталонным рядам относятся: гармонический ряд, обобщенно гармонический ряд, ряд геометрической прогрессии.

Ряд геометрической прогрессии.

Исследуем сходимость ряда

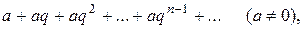(6)

который называется рядом геометрической прогрессии.

Как известно, сумма первых n членов прогрессии находится по формуле 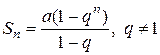. Найдем предел этой суммы:

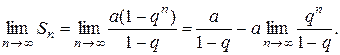
Рассмотрим следующие случаи в зависимости от величины q:

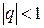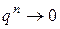1. Если , то при 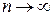. Поэтому 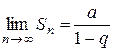, ряд (6) сходится, его сумма равна ;

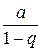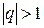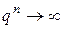2. Если , то при 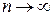. Поэтому 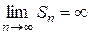, ряд (6) расходится;

3. Если 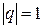, то 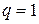ряд (6) принимает вид 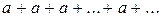, для него 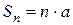и 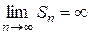; т. е. ряд (6) расходится; при 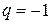ряд (6) принимает вид 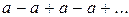– в этом случае 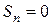при четном n и 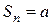при нечетном n. Следовательно, 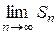не существует, ряд (6) расходится.

Def: Ряд геометрической прогрессии сходится при 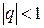и расходится при .

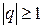Пример 1: Показать, что ряд 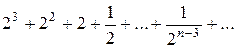сходится.

Решение. Данный ряд можно переписать так:

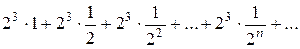Как видно, он представляет собой ряд геометрической прогрессии с 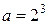и 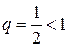. Этот ряд сходится согласно свойству 1 числовых рядов.

Остальные эталонные ряды рассмотрим с доказательствами их сходимости далее, по мере введения достаточных признаков сходимости.

Необходимое условие сходимости

Нахождение n-й частичной суммы S_n и ее предела для произвольного ряда во многих случаях является непростой задачей. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости. Первым из них, как правило, является необходимый признак сходимости.

Th: Если ряд (1) сходится, то его общий член 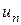стремится к нулю, т. е. .

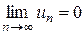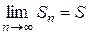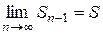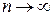Доказательство: Пусть ряд (1) сходится и . Тогда и (при и 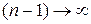). Учитывая, что 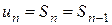при 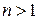, получаем:

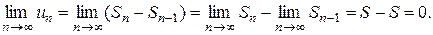
Что и требовалось доказать.

Следствие (достаточное условие расходимости ряда). Если 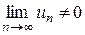или этот предел не существует, то ряд расходится.

Доказательство: Действительно, если бы ряд сходился, то (по теореме) 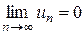. Но это противоречит условию. Значит, ряд расходится.

Пример 2: Исследовать сходимость ряда .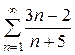

Решение. Ряд 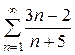расходится, т. к.

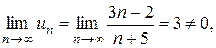
т. е. выполняется достаточное условие расходимости ряда.

Пример 3: Исследовать сходимость ряда

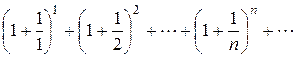Решение. Данный ряд расходится, т. к.

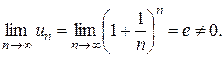
Теорема дает необходимое условие сходимости ряда, но не достаточное: из условия 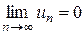не следует, что ряд сходится. Это означает, что существуют расходящиеся ряды, для которых .

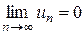В качестве второго примера можно взять ряд

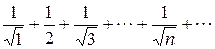Здесь 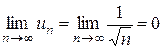. Однако, этот ряд расходится.

Доказательство: Действительно,

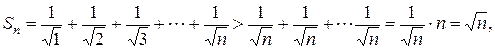
т. е. 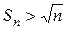. Следовательно, 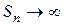при 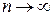, ряд расходится.

Что и требовалось доказать.