ЛЕКЦИЯ №11. Тема 9.2. Достаточные признаки сходимости рядов с положительными членами: 1) Признаки сравнения. 2) Признак Даламбера. 3) Алгебраический (радикальный) признак Коши. 4) Интегральный признак Коши. 5) Обобщенный гармониче

ЛЕКЦИЯ №11

Тема 9. 2. Достаточные признаки сходимости рядов с положительными членами: 1) Признаки сравнения. 2) Признак Даламбера. 3) Алгебраический (радикальный) признак Коши. 4) Интегральный признак Коши. 5) Обобщенный гармонический ряд.

Достаточные признаки сходимости

Необходимый признак сходимости не дает, вообще говоря, возможности судить о том, сходится ли данный ряд или нет. Сходимость и расходимость ряда во многих случаях можно установить с помощью так называемых достаточных признаков.

Def: Для знакоположительных рядов, т. е. рядов с неотрицательными членами (знакоотрицательный ряд переходит в знакоположительный путем умножения его на (–1), что как известно, не влияет на сходимость ряда).

Признаки сравнения рядов.

Сходимость или расходимость знакоположительного ряда часто устанавливается путем сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет. В основе такого сравнения лежат следующие теоремы.

Th 1: Пусть даны два положительных ряда

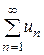(8)

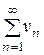. (9)

Если для всех n выполняется неравенство

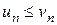, (10)

то из сходимости ряда (9) следует сходимость ряда (8), из расходимости ряда (8) следует расходимость ряда (9).

Доказательство: Обозначим n-е частичные суммы рядов (8) и (9) соответственно через 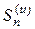и 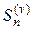. Из неравенства (10) следует, что

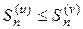. (11)

Пусть ряд (9) сходится и его сумма равна 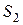. Тогда . Члены ряда (9) положительны, поэтому 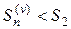и, следовательно, с учетом неравенства (10), 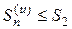. Таким образом, последовательность 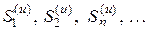монотонно возрастает 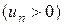и ограничена сверху числом 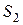. По признаку существования предела последовательность 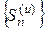имеет предел 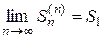, т. е. ряд (8) сходится.

Пусть теперь ряд (8) расходится. Так как члены ряда неотрицательны, в этом случае имеем 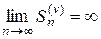, т. е. ряд (9) расходится.

Что и требовалось доказать.

Замечание: Теорема 1 справедлива и в том случае, когда неравенство (10) выполняется не для всех членов рядов (8) и (9), а начиная с некоторого номера N. Это вытекает из свойства 3 числовых рядов.

Th 2 (предельный признак сравнения): Пусть даны два положительных ряда (8) и (9). Если существует конечный, отличный от нуля, предел 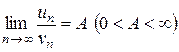, то ряды (8) и (9) сходятся или расходятся одновременно.

Доказательство: По определению предела последовательности для всех n, кроме, возможно, конечного числа их, для любого 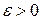выполняется неравенство 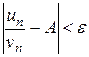, или

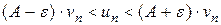. (12)

Если ряд (8) сходится, то из левой части неравенства (12) и теоремы 1 вытекает, что ряд 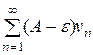также сходится. Но тогда, согласно свойству 1 числовых рядов, ряд (9) расходится.

Аналогично, если ряд (9) сходится (расходится), то сходящимся (расходящимся) будет и ряд (8).

Пример 1: Исследовать на сходимость ряд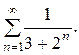

Решение. Сравним данный ряд с рядом геометрической прогрессии 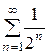, который сходится . Имеем . Следовательно, данный ряд сходится.

Пример 2: Исследовать сходимость ряда

Решение. Здесь 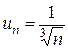. Возьмем ряд с общим членом 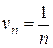, который расходится (гармонический ряд). Имеем 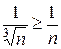. Следовательно, данный ряд расходится.

Пример 3: Исследовать сходимость ряда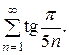

Решение. Применим предельный признак сравнения. Так как 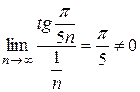, то по теореме 2 исходный ряд расходится, как сравнимый с гармоническим рядом.

Признак Даламбера.

В отличие от признаков сравнения, где все зависит от догадок и запаса известных сходящихся и расходящихся рядов, признак Даламбера (1717-1783, французский математик) позволяет часто решить вопрос о сходимости ряда, проделав лишь некоторые операции над самим рядом.

Th 3: Пусть дан ряд (1) с положительными членами и существует конечный или бесконечный предел . Тогда ряд сходится при 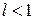и расходится при .

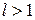Доказательство: Так как , то по определению предела для любого 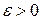найдется натуральное число N такое, что при 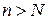выполняется неравенство

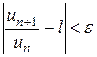или 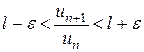. (13)

Пусть 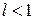. Можно подобрать 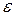так, что число 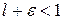. Обозначим . Тогда из первой части неравенства (13) получаем 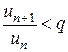, или 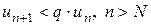. В силу свойства 3 числовых рядов можно считать, что 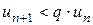для всех . Давая номеру n эти значения, получим серию неравенств:

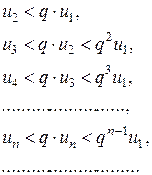
т. е. члены ряда 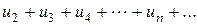меньше соответствующих членов ряда 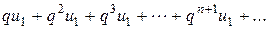, который сходится как ряд геометрической прогрессии со знаменателем 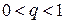. Но тогда, на основании признака сравнения, сходится ряд , следовательно, сходится и исходный ряд (1).

Пусть 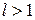. В этом случае 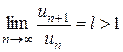. Отсюда следует, что, начиная с некоторого номера N, выполняется неравенство 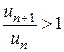, или 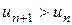, т. е. члены ряда возрастают с увеличением номера n. Поэтому 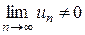. На основании следствия из необходимого признака ряд (1) расходится.

Что и требовалось доказать.

Замечание 1. Если 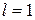, то ряд (1) может быть как сходящимся, так и расходящимся.

Замечание 2. Признак Даламбера целесообразно применять, когда общий член ряда содержит выражение вида n! или aⁿ.

Пример 4: Исследовать на сходимость ряд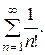

Решение. Находим

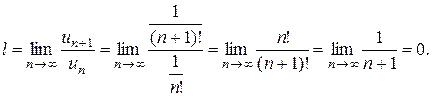
Так как 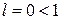, то данный ряд по признаку Даламбера сходится.

Пример 5: Исследовать сходимость ряда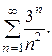

Решение. Вычисляем

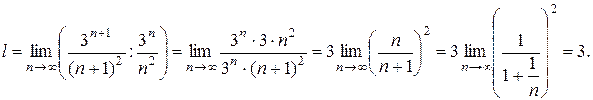
Так как 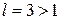, то данный ряд по признаку Даламбера сходится.

Радикальный признак Коши.

Иногда удобно пользоваться радикальным признаком Коши для исследования сходимости знакоположительного ряда. Этот признак во многом схож с признаком Даламбера, о чем говорят его формулировка и доказательство.

Th 4: Пусть дан ряд (1) с положительными членами и существует конечный или бесконечный предел 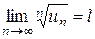. Тогда ряд сходится при 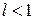и расходится при .

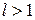Как и для признака Даламбера, в случае, когда 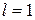, вопрос о сходимости ряда остается открытым. Доказательство теоремы аналогично доказательству признака Даламбера. Поэтому опусти его.

Пример 6: Исследовать на сходимость ряд .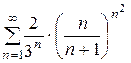

Решение. Так как

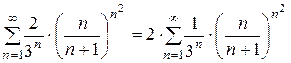то применим радикальный признак Коши к ряду

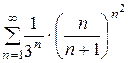Вычисляем

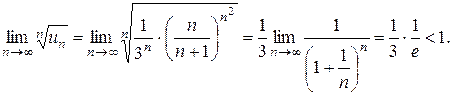
Ряд 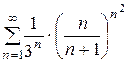сходится, а значит, сходится и исходный ряд, согласно свойству 1 числовых рядов.

Интегральный признак Коши. Обобщенный гармонический ряд.

Th 5: Если члены знакоположительного ряда 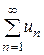могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей на промежутке 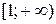функции так, ч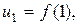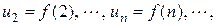то то:

1) если 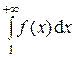сходится, то сходится и ряд (1);

2) если 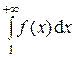расходится, то расходится и ряд (1).

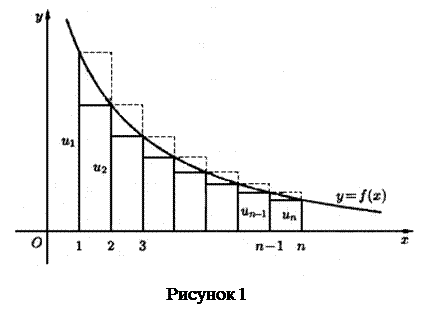Доказательство: Рассмотрим криволинейную трапецию, ограниченную сверху графиком функции , основанием которой служит отрезок оси Ох от 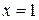до 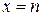(рисунок 1).

Построим входящие и выходящие прямоугольники, основаниями которых служат отрезки [1; 2], [2; 3], …. Учитывая геометрический смысл определенного интеграла, запишем:

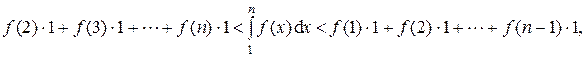
или

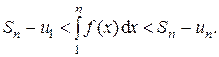(14)

Случай 1. Несобственный интеграл 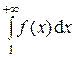сходится, т. е. 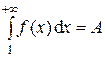. Поскольку 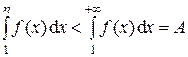, то с учетом неравенства (14) имеем: 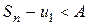, т. е. . Так последовательность частичных сумм монотонно возрастает и ограничена сверху (числом ), то по признаку существования предела, имеет предел. Следовательно, ряд (1) сходится.

Случай 2. Несобственный интеграл 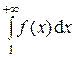расходится. Тогда 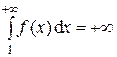и интегралы неограниченно возрастают при . Учитывая, что 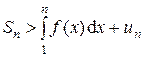, получаем, что 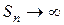при . Следовательно, данный ряд (1) расходится.

Что и требовалось доказать.

Замечание. Вместо интеграла 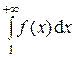можно брать интеграл 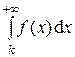, где 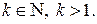Отбрасывание k первых членов ряда в ряде (1), как известно, не влияет на сходимость (расходимость) ряда.

Пример 7: Исследовать на сходимость ряд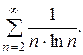

Решение. Воспользуемся интегральным признаком Коши. Функция 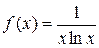удовлетворяет условиям теоремы 5. Находим

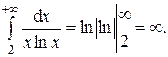
Значит, ряд с общим числом 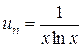расходится.

Ряд

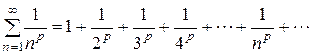, (15)

где – действительное число, называется обобщенным гармоническим рядом. Для исследования ряда (15) на сходимость применим интегральный признак Коши (признаки Даламбера и Коши ответа о сходимости не дают).

Рассмотрим функцию 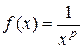. Эта функция непрерывна, монотонно убывает на промежутке 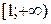и . При 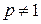имеем:

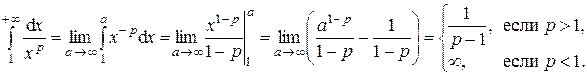
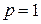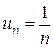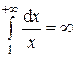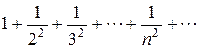При получаем гармонический ряд , который расходится (второй способ: ). Итак, ряд (15) сходится при , расходится при . В частности, ряд сходится (полезно знать).

Рассмотренные признаки сходимости (есть и другие) знакоположительных рядов позволяют судить о сходимости практически любого знакоположительного ряда. Необходимые навыки приобретаются на практике.