
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
КОНТРОЛЬНАЯ РАБОТА № 1
1. Вычислить определитель
А) 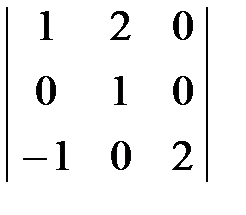 . Б)
. Б)  .
.
Решение:
А) Вычислим определитель путем разложения по первой строке, используя формулу:
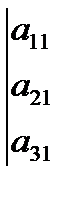
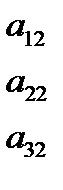
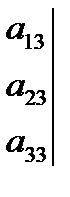 =
= 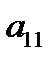 ∙
∙ 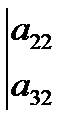
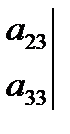 -
- 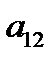 ∙
∙ 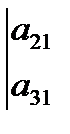
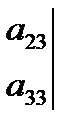 +
+ 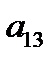 ∙
∙ 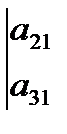
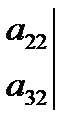 - разложение определителя третьего порядка по элементам первой строки.
- разложение определителя третьего порядка по элементам первой строки.
Определители второго порядка вычисляются по формуле:
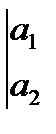
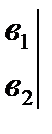 =
= 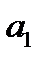 ∙
∙ 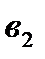 -
- 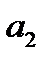 ∙
∙ 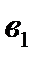
Элементы 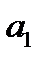 ,
, 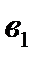 ,
, 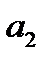 ,
, 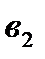 в определителе (2) образуют форму квадрата. Диагональ, на которой находится элементы
в определителе (2) образуют форму квадрата. Диагональ, на которой находится элементы 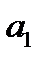 ,
, 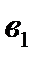 - главная, а диагональ, на которой находятся элементы
- главная, а диагональ, на которой находятся элементы 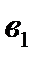 ,
,  - побочная.
- побочная.
Общая формула разложения определителя третьего порядка.
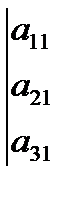
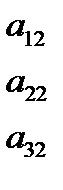
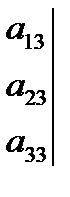 =
= 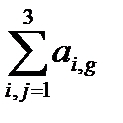 ∙ Аi, j=
∙ Аi, j= 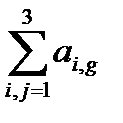 ∙ (–1)i+j ∙ Mi, j,
∙ (–1)i+j ∙ Mi, j,
Аi, j – алгебраическое дополнение (адъюнкт) элемента 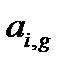 в определителе, равное произведению минора Mi, j (определителя) второго порядка полученного вычеркиванием i-ой строки и j – столбца в определителе на
в определителе, равное произведению минора Mi, j (определителя) второго порядка полученного вычеркиванием i-ой строки и j – столбца в определителе на
(–1)i+j, 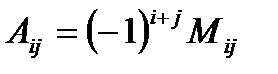 .
.
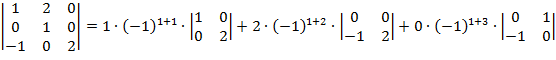 =1
=1 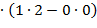 -2
-2 
Таким образом, 
Б) Вычислим данный определитель, путем разложения по элементам первого столбца:
 =
= 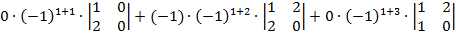 =0
=0 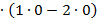 -1
-1 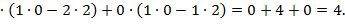
Таким образом,  =4
=4
Ответ: А)  ; Б)
; Б)  =4
=4
2. Решить систему методом обратной матрицы
А) 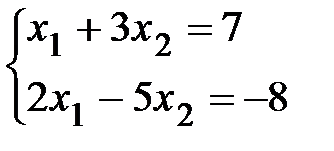 б)
б) 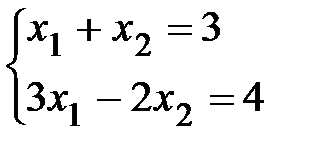
Решение:
А) 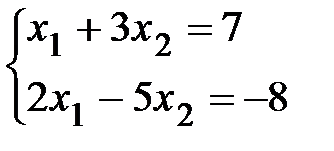
Рассмотрим квадратную матрицу второго порядка и найдем к ней обратную.
Пусть 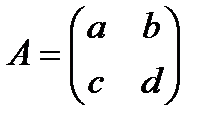 и DA=det A, тогда обратная матрица к матрице А имеет вид:
и DA=det A, тогда обратная матрица к матрице А имеет вид: 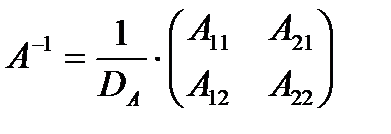
А11=(-1)1+1∙ d=d, А12=(-1)1+2∙ c=-c, А21=(-1)2+1∙ b=-b, А22=(-1)2+2∙ a=a,
Имеем, что 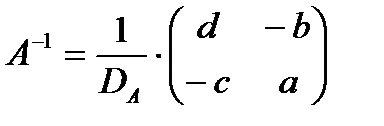
Составим и вычислим определитель системы:
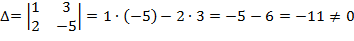 , следовательно существует обратная матрица и система имеет единственное решение.
, следовательно существует обратная матрица и система имеет единственное решение.
А11=(-1)1+1∙ (-5)=-5, А12=(-1)1+2∙ 2=-2, А21=(-1)2+1∙ 3=-3, А22=(-1)2+2∙ 1=1,
Имеем, что 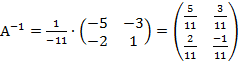
Исходную систему уравнений можно записать в виде матричного уравнения
А 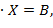 где
где 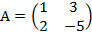 ,
, 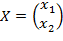 и
и 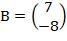 .
.
Тогда решение матричного уравнения будем находить по формуле:
Х= 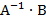 , где
, где 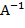 - обратная матрица к матрице А. Умножение матриц некоммутативно, поэтому умножаем матрицу В на обратную матрицу
- обратная матрица к матрице А. Умножение матриц некоммутативно, поэтому умножаем матрицу В на обратную матрицу 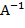 слева.
слева.
Х= 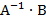 =
= 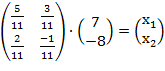
Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В. Находим матрицу С=АВ, элементы которой определяются по формуле
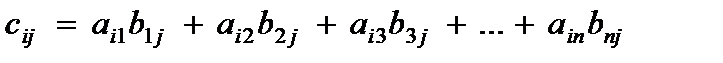 .
.
Учитывая последнюю формулу, получаем:
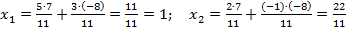 =2.
=2.
Таким образом, 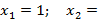 2.
2.
Б) 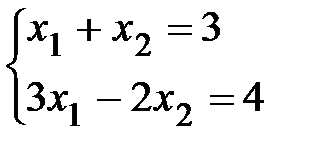
Решение: Составим и вычислим определитель системы:
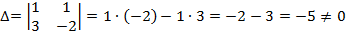 , следовательно существует обратная матрица и система имеет единственное решение.
, следовательно существует обратная матрица и система имеет единственное решение.
А11=(-1)1+1∙ (-2)=-2, А12=(-1)1+2∙ 3=-3, А21=(-1)2+1∙ 1=-1, А22=(-1)2+2∙ 1=1,
Имеем, что 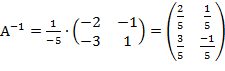
Исходную систему уравнений можно записать в виде матричного уравнения
А 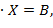 где
где 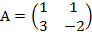 ,
, 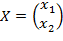 и
и 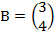 .
.
Тогда решение матричного уравнения будем находить по формуле:
Х= 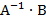 , где
, где 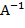 - обратная матрица к матрице А.
- обратная матрица к матрице А.
Х= 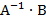 =
= 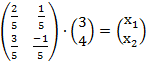
Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В. Находим матрицу С=АВ, элементы которой определяются по формуле
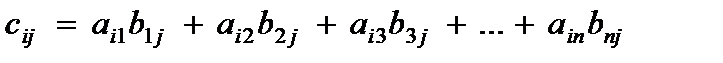 .
.
Учитывая последнюю формулу, получаем:
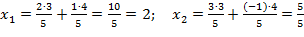 =1.
=1.
Таким образом, 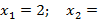 1.
1.
Ответ: А) 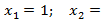 2.
2.
Б) 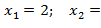 1.
1.
3. Исследовать систему
А) 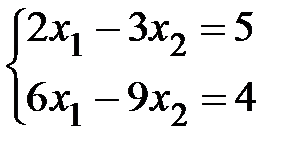 б)
б) 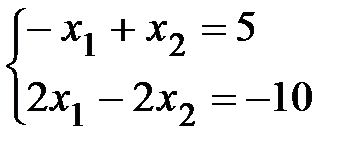
Решение:
А) 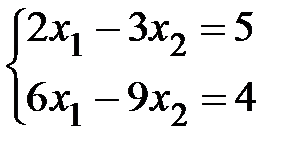
Составим и вычислим определитель системы:
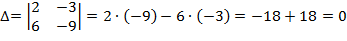
Так как определитель системы равен нулю, то возможно два варианта:
1) система имеет бесчисленное множество решений, если 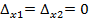 , где
, где  - определители, полученные из определителя системы путем замены переменных соответственно первого и второго столбца столбцом свободных членов;
- определители, полученные из определителя системы путем замены переменных соответственно первого и второго столбца столбцом свободных членов;
2) система не имеет решения, если 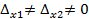 .
.
Составим и вычислим определители:
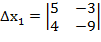 =5
=5 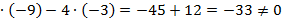
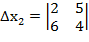 =2
=2 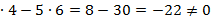 .
.
Следовательно, данная система не совместна, т. е. не имеет решения.
Б) 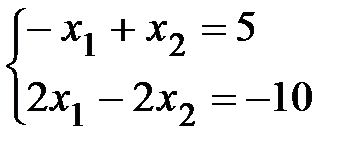
Решение: Составим и вычислим определитель системы:
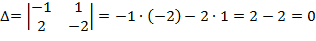
Так как определитель системы равен нулю, то возможно два варианта:
1) система имеет бесчисленное множество решений, если 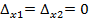 , где
, где  - определители, полученные из определителя системы путем замены переменных соответственно первого и второго столбца столбцом свободных членов;
- определители, полученные из определителя системы путем замены переменных соответственно первого и второго столбца столбцом свободных членов;
2) система не имеет решения, если 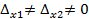 .
.
Составим и вычислим определители:
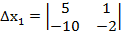 =5
=5 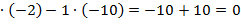
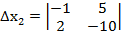 =-1
=-1 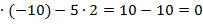 .
.
Следовательно, данная система совместна и имеет бесконечное множество решений.
Ответ:
А) система не совместна, т. е. не имеет решения;
Б) система имеет бесконечное множество решений.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ
№1. Найти значение выражения
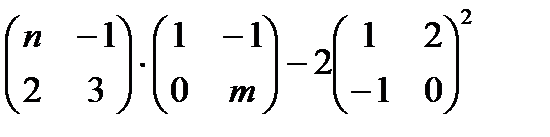 ,
,
Здесь n – число гласных в фамилии
m – число согласных в фамилии
Решение: Имеем n=4, m=4
Найдем значение выражения
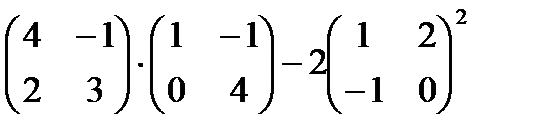
Запишем в виде матричного выражения: 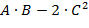
1)Найдем D= 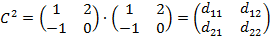
Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В. Находим матрицу С=АВ, элементы которой определяются по формуле
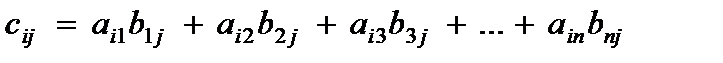 .
.
По последней формуле определяем элементы матрицы D.
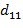 =
= 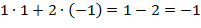 ;
; 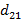 =
= 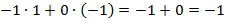 ;
;
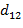 =
= 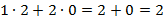 ;
; 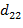 =-
=- 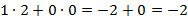 .
.
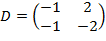
2)Найдем произведение матриц 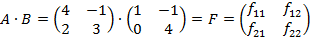
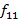 =
= 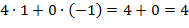 ;
; 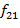 =
= 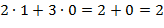 ;
;
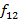 =
= 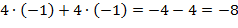 ;
; 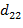 =-
=- 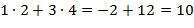 .
.
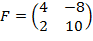
3)Найдем матрицу G=2 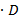 =2
=2 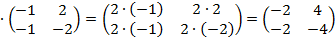
4) Найдем матрицу
К=F-G= 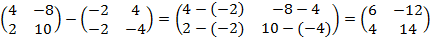
Ответ: 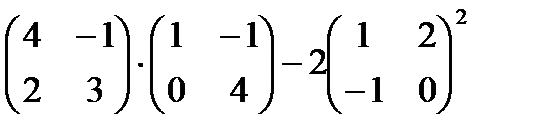 =
= 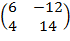
№2. Вычислить
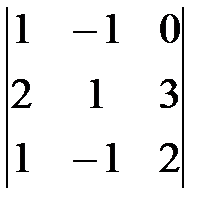 .
.
Решение:
Вычислим определитель по формуле
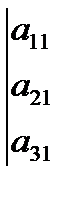
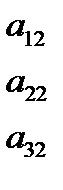
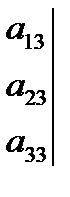 =
= 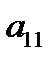 ∙
∙ 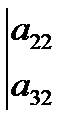
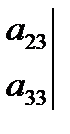 -
- 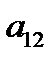 ∙
∙ 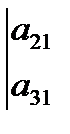
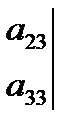 +
+ 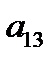 ∙
∙ 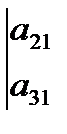
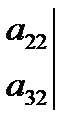 - разложения определителя третьего порядка по элементам первой строки.
- разложения определителя третьего порядка по элементам первой строки.
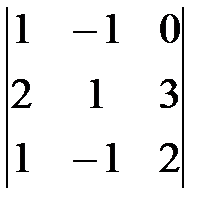 =1
=1 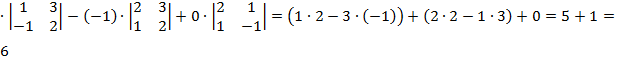 .
.
Учитывая, что определители второго порядка находятся по формуле:
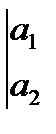
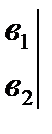 =
= 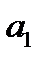 ∙
∙ 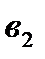 -
- 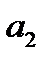 ∙
∙ 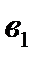
Ответ: 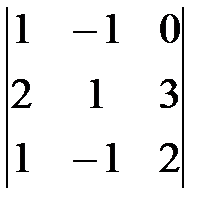 =6
=6
№3 Решить неравенство
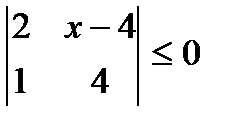
Решение:
Используя формулу нахождения определителя второго порядка
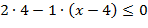
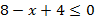
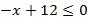
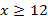
Ответ: 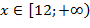
№4 Вычислить определитель
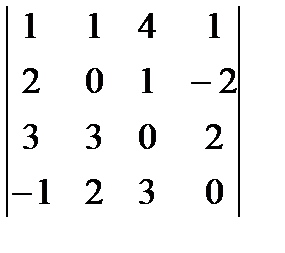
Решение:
Вычислим определитель, разложив его по элементам первой строки:
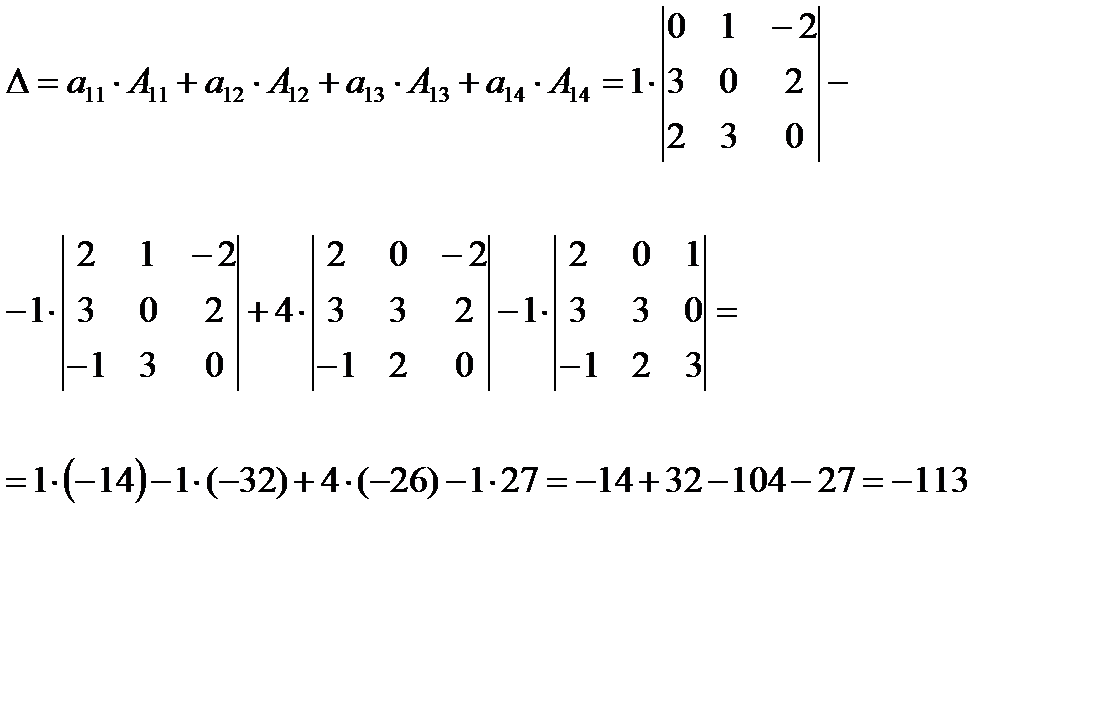 Вычислим определители третьего порядка, являющиеся минорами для исходного определителя.
Вычислим определители третьего порядка, являющиеся минорами для исходного определителя.
Вычисляем данные определители разложением путем разложения определителя по первой строке.
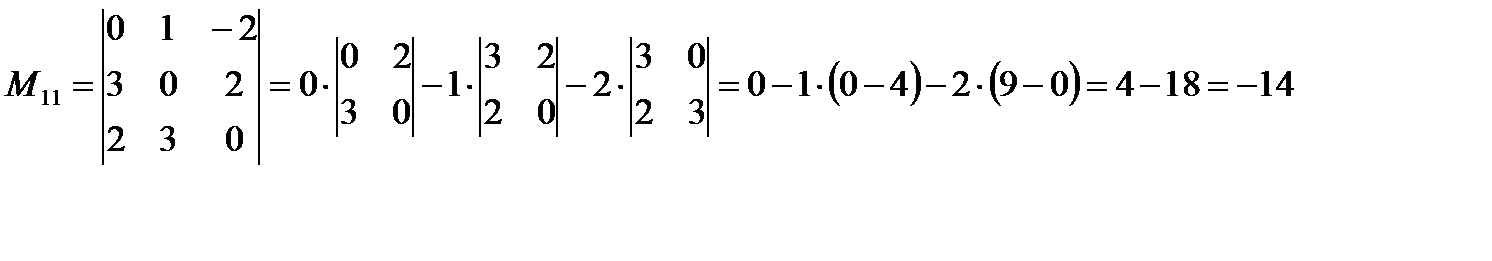
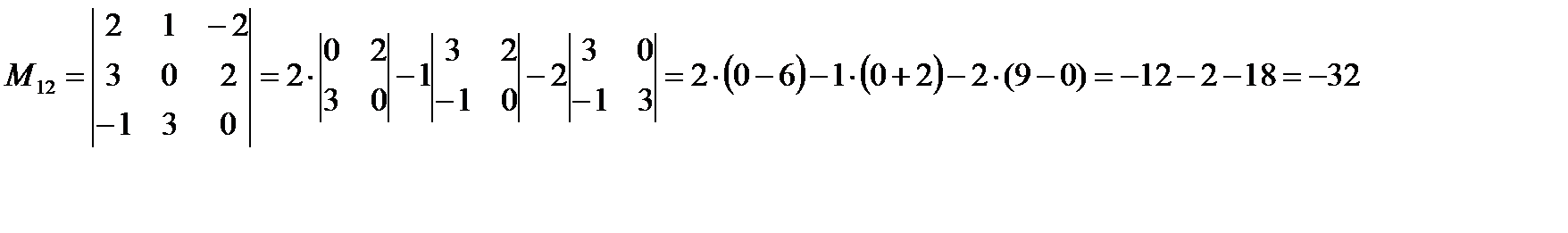
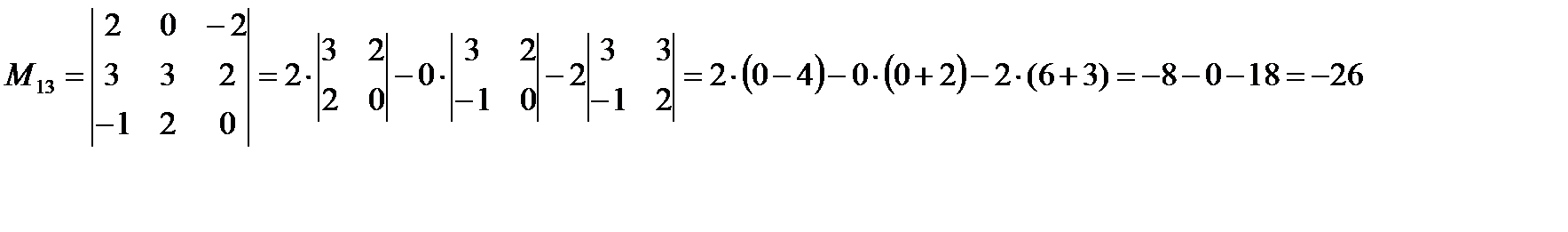
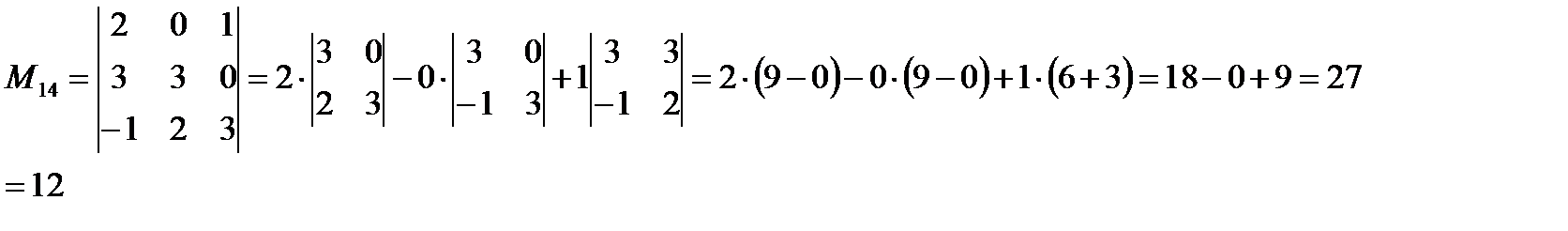 Ответ:
Ответ: 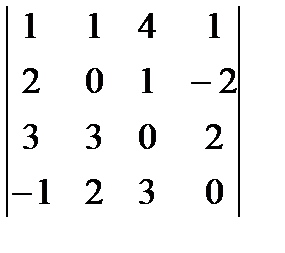 =-113
=-113
№5 Найти обратную матрицу к матрице А
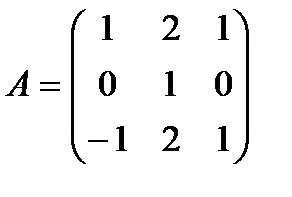
Решение:
а) Обратная матрица  матрицы А имеет вид
матрицы А имеет вид
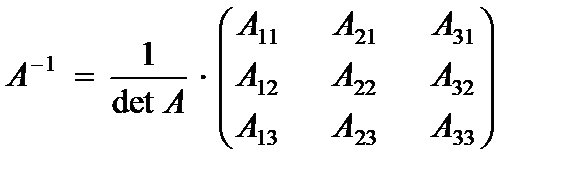
где 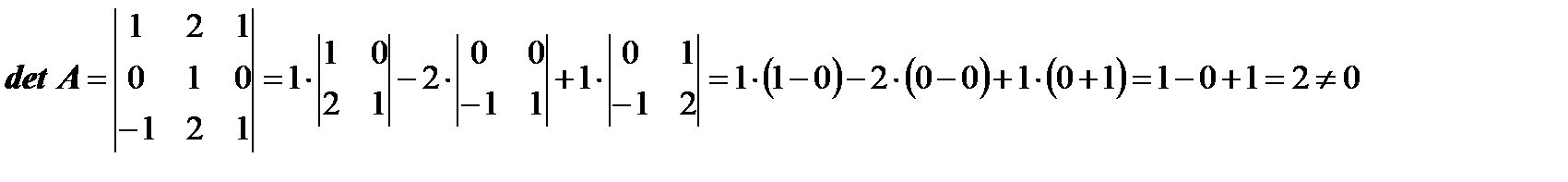
т. е. матрица A - невырожденная, и, значит, существует матрица 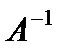
Найдем алгебраические дополнения к элементам матрицы A, где Аi, j – алгебраическое дополнение (адъюнкт) элемента 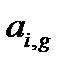 в определителе, равное произведению минора Mi, j (определителя) второго порядка полученного вычеркиванием i-ой строки и j – столбца в определителе на
в определителе, равное произведению минора Mi, j (определителя) второго порядка полученного вычеркиванием i-ой строки и j – столбца в определителе на
(–1)i+j, 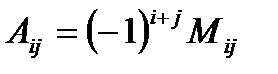
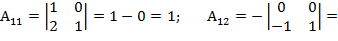 0-0=0;
0-0=0; 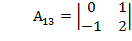 =0+1= 1
=0+1= 1
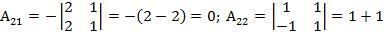 =2;
=2; 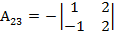 =
= 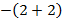 = -4
= -4
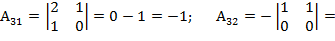 -
- 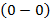 = 0;
= 0; 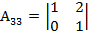 =1-0= 1
=1-0= 1
Тогда обратная матрица имеет вид:
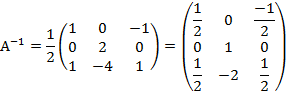
Ответ:
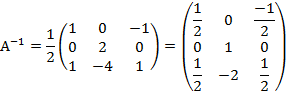
№6. Найти ранг матрицы

Решение:
Рангом матрицы называют максимальное число линейно независимых строк или наибольший порядок минора этой матрицы, отличный от нуля
Чтобы определить ранг матрицы приведем ее к треугольному (диагональному) ступенчатому виду с помощью элементарных преобразований, к которым относят:
1)перестановка любых строк матрицы;
2) умножение любой строки на число, не равное нулю;
3) вычеркивание строки, состоящей из одних нулей;
4) вычитание из любой строки, любой другой, умноженной на число, отличное от нуля.
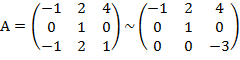
1)К 3 строке прибавим 1 строку, умноженную на (-1)
Получаем rang A=3.
Или вычислим миноры этой матрицы.
А) Минор 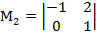 =(-1)
=(-1) 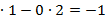
Б) Его окаймляет минор 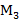 =
= 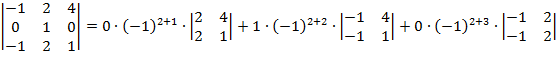 =0+1
=0+1 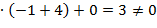 .
.
Так как наивысший порядок минора отличного от нуля равен 3, то ранг матрицы А тоже равен 3.
Ответ: rang A=3
№7. Найти решение системы тремя методами
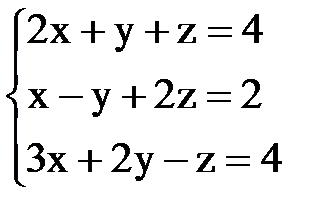 .
.
Решение:
1) Реши м систему методом Крамера. Для этого используем формулы Крамера:
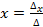 ;
; 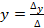 ;
;  .
.
Где  -определитель системы, определитель, составленный из коэффициентов при неизвестных.
-определитель системы, определитель, составленный из коэффициентов при неизвестных.
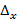 ,
, 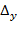 и
и 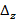 - определители, полученные путем замены коэффициентов при соответственных неизвестных столбцом свободных членов.
- определители, полученные путем замены коэффициентов при соответственных неизвестных столбцом свободных членов.
Составим и вычислим определитель системы, путем разложения по первой строке:
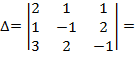 2
2 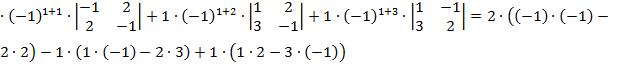 =2
=2  -1
-1 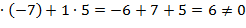
Таким образом, 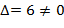 , следовательно система совместна и имеет единственное решение.
, следовательно система совместна и имеет единственное решение.
Найдем определители:
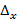 =
= 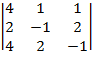 =4
=4 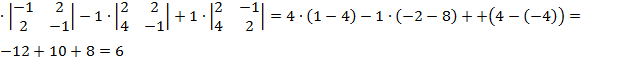
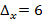
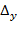 =
= 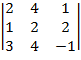 =2
=2 
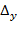 =6
=6
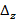 =
= 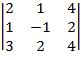 =2
=2 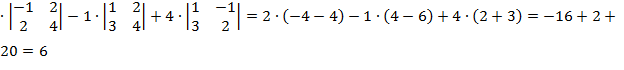
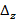 =6
=6
Подставляя полученные значения в формулы Крамера, получаем значения переменных:
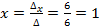 ;
; 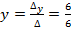 =1;
=1; 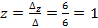 .
.
.
Ответ: (1; 1; 1)
2) Решим систему с помощью обратной матрицы.
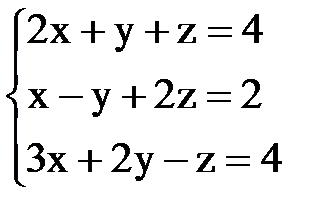
Данную систему уравнений можно переписать в виде матричного уравнения:
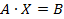 , где А=
, где А= 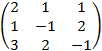 ,
, 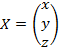 и
и 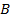 =
= 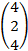
Тогда решение матричного уравнения будем искать в виде:  , где
, где 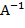 -матрица, обратная к матрице А.
-матрица, обратная к матрице А.
А) Найдем обратную матрицу 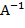 .
.
Найдем определитель матрицы:
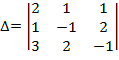 =2
=2  -1
-1 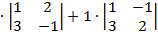 =2
=2 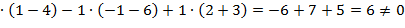
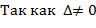 , следовательно матрица А невырожденная, т. е. существует обратная.
, следовательно матрица А невырожденная, т. е. существует обратная.
Обратная матрица 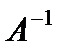 матрицы А имеет вид
матрицы А имеет вид
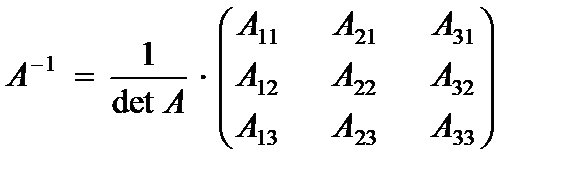
Найдем алгебраические дополнения к элементам матрицы A, где Аi, j – алгебраическое дополнение (адъюнкт) элемента 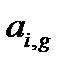 в определителе, равное произведению минора Mi, j (определителя) второго порядка полученного вычеркиванием i-ой строки и j – столбца в определителе на
в определителе, равное произведению минора Mi, j (определителя) второго порядка полученного вычеркиванием i-ой строки и j – столбца в определителе на
(–1)i+j, 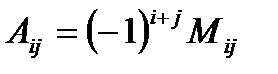
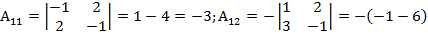 =7;
=7; 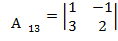 =2+3= 5
=2+3= 5
 =-5;
=-5; 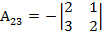 =
= 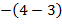 = -1
= -1
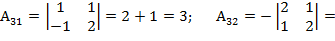 -
- 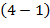 = -3;
= -3; 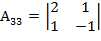 =-2-1= -3
=-2-1= -3
Тогда обратная матрица имеет вид:
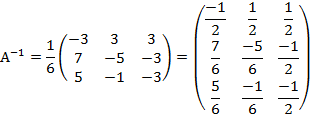
Х= 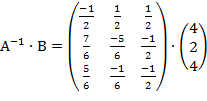 =
= 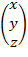
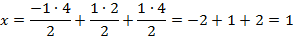
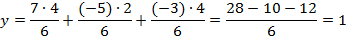
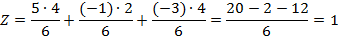
Ответ: (1; 1; 1)
3) Решим систему уравнений методом Гаусса
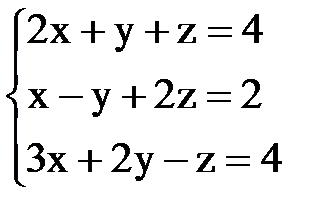
Составим расширенную матрицу системы и приведем ее при помощи элементарных преобразований к диагональному (ступенчатому) виду.
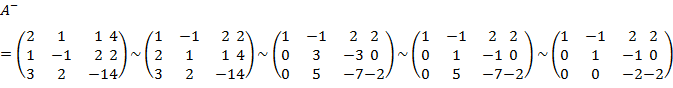
1)Поменяем местами 1 и 2 строки.
2)а) к 2 строке прибавить 1 строку, умноженную на 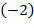 ;
;
Б) к 3 строке прибавить 1 строку, умноженную на (-3).
3) Разделим вторую строку на 3.
4) к 3 строке прибавить 2 строку, умноженную на (-5)
Таким образом, получаем систему, равносильную данной:
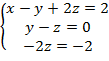 Применяя обратный ход метода Гаусса, последовательно получаем:
Применяя обратный ход метода Гаусса, последовательно получаем:
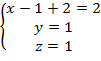
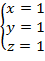
Ответ: (1; 1; 1)
ЭКЗАМЕНАЦИОННЫЙ ТЕСТ
Вариант ___1___
1. Вычислите значение матричного выражения

Решение: Запишем данное матричное выражение в виде:
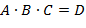
1)Найдем матрицу F
F= 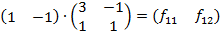
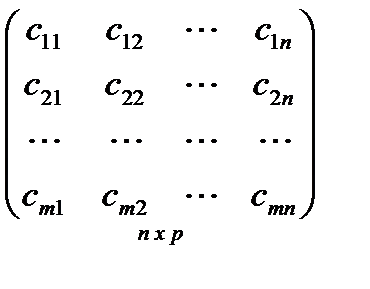
Т. к. произведением матрицы А, имеющей размерность m х n, на матрицу В имеющей размерность n x p называется матрица С, имеющая размерность m x p, и элементы матрицы С определяются следующей формулой:
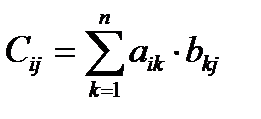 , i=1, 2, …, m, j=1, 2, …, p.
, i=1, 2, …, m, j=1, 2, …, p.
 ∙
∙  =
= 
Получаем
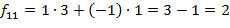
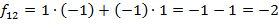
Таким образом, 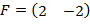
Найдем матрицу D
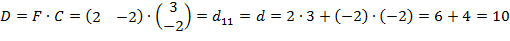
Ответ:
 = 10
= 10
2. Значением определителя 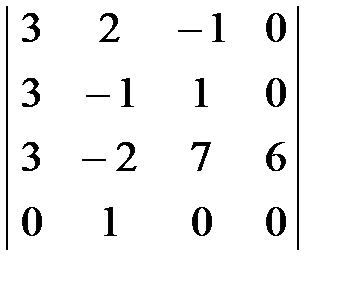 является
является
Решение:
Вычислим определитель, разложив его по элементам четвертой строки:
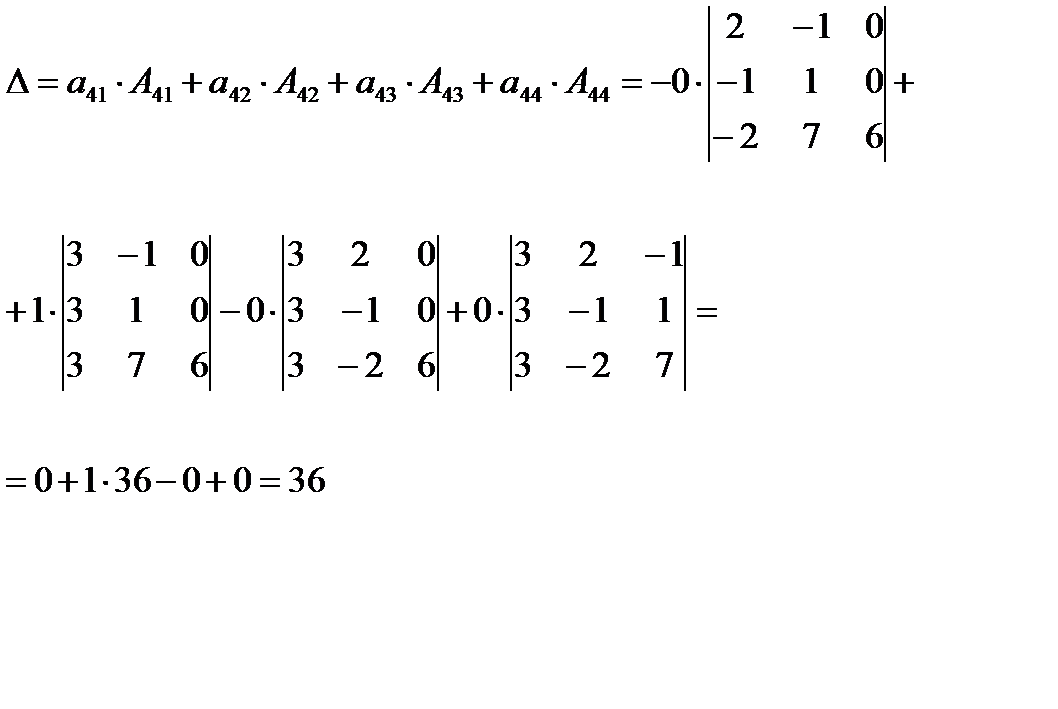 Т. к. первое, третье и четвертое слагаемое в определители обращается в нуль, то можно не вычислять определители третьего порядка, входящие в эти слагаемые.
Т. к. первое, третье и четвертое слагаемое в определители обращается в нуль, то можно не вычислять определители третьего порядка, входящие в эти слагаемые.
Вычисляем определитель второго слагаемого путем разложения его по третьему столбцу.
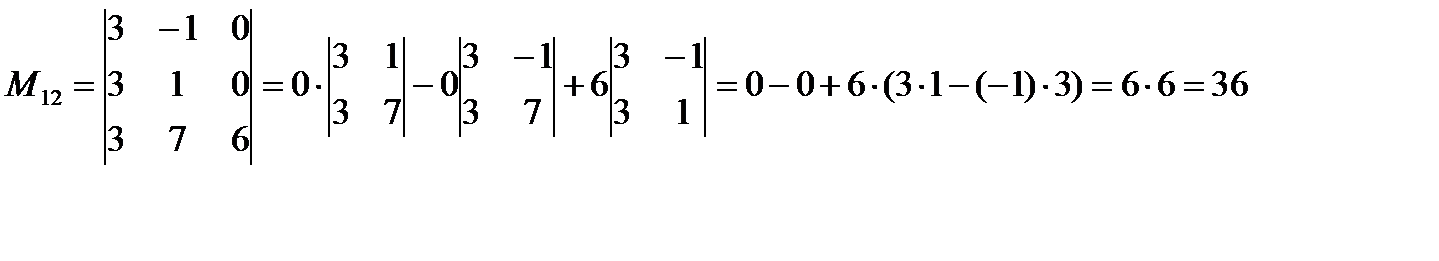
Ответ:  =36
=36
3. Прямые 2х - 5у - 3 = 0 и у = kx − 1 параллельны, если
k равно________
1) 2/5 2) 2, 5 3) – 0. 4 4) –2, 5 5) 1, 25
Решение:
Выразим из первого уравнения у, 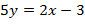 ,
, 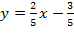 .
.
Условие параллельности двух прямых 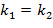 . Следовательно
. Следовательно 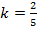 .
.
Ответ: 1) 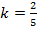
4. Дано общее уравнение плоскости
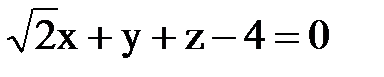 ,
,
найти значения направляющих косинусов.
Решение:
Согласно нормальному уравнению плоскости
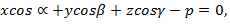 где
где 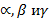 -углы, образованные перпендикуляром с осями координат Оx, Oy и Oz; р – длина перпендикуляра.
-углы, образованные перпендикуляром с осями координат Оx, Oy и Oz; р – длина перпендикуляра.
Тогда имеем 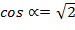 ;
; 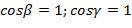 .
.
Ответ: 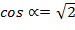 ;
; 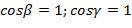 .
.
ЭКЗАМЕНАЦИОННЫЙ ТЕСТ
Вариант ___2___
1. Найти значение выражения А2, если 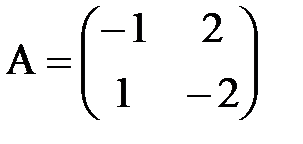 .
.
Решение:
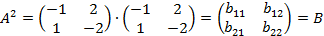
Т. к. произведением матрицы А, имеющей размерность m х n, на матрицу В имеющей размерность n x p называется матрица С, имеющая размерность m x p, и элементы матрицы С определяются следующей формулой:
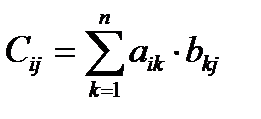 , i=1, 2, …, m, j=1, 2, …, p.
, i=1, 2, …, m, j=1, 2, …, p.
 ∙
∙ 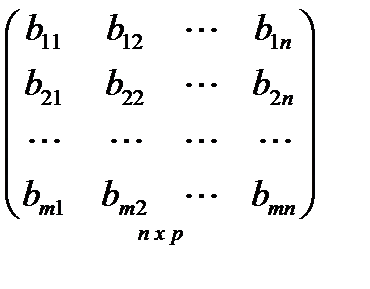 =
= 
Получаем
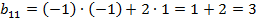
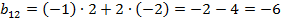
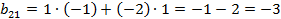
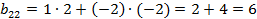
Таким образом, 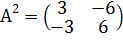
Ответ: 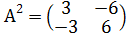
2. Значением определителя 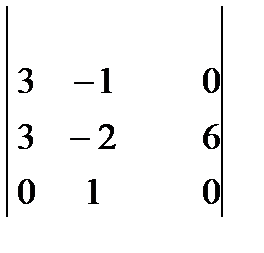 является
является
Решение:
Вычислим определитель разложением по третьему столбцу

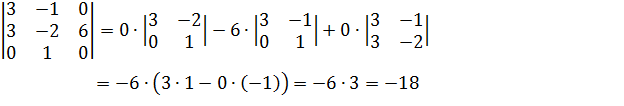
Ответ:  =-18
=-18
3. Вектор 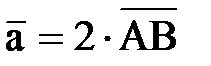 , если А(2; 1; 1) и В(− 1; 2; 3), то длина
, если А(2; 1; 1) и В(− 1; 2; 3), то длина
вектора______
Решение: Найдем сначала координаты вектора 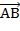 , по формуле
, по формуле
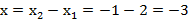
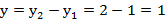
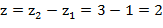
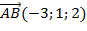
Найдем координаты вектора 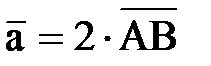 =
= 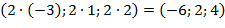
Длину искомого вектора найдем по формуле:
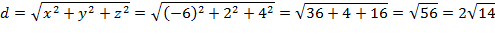
Ответ: 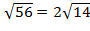
4. Даны координаты вершин пирамиды А1А2А3А4:
А1(2; 4; 3), А2(7; 6; 3), А3(4; 9; 3), А4(3; 6; 7).
Найти уравнение прямой А1А2
Решение:
Уравнение прямой, проходящей через две заданные точки А1(х1, y1, z1) и А2(х2, y2, z2) имеет вид
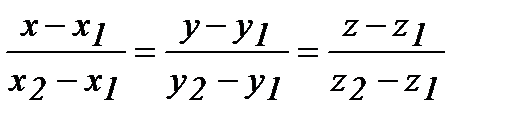
Подставив в данное уравнение координаты точек А1 и А2, получим
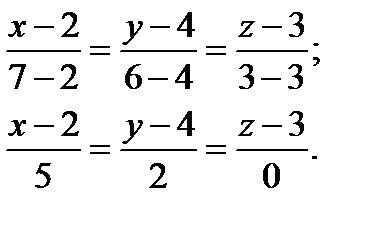
Ответ: 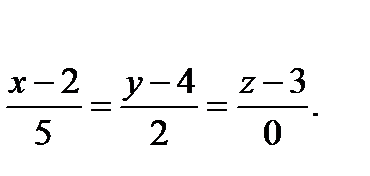
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|