- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
2. Трудности, порождаемые нелинейностями.
1. Типы нелин-х задач.
Наиболее полно изученными имеющими формализуемые методы решения являются задачи с линейными ограничениями и нелинейной ЦФ. В общем виде задача нелинейного программирования выглядит:
Найти максимум или минимум 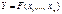 при
при   Даже для задач с лин-ми огр-ми корректные вычисл-ые процедуры разработаны лишь для тех случаев, когда на ЦФ наложены достаточно жесткие ограничения:
1) ЦФ м. б. записана как сумма n от одной переменной:
Даже для задач с лин-ми огр-ми корректные вычисл-ые процедуры разработаны лишь для тех случаев, когда на ЦФ наложены достаточно жесткие ограничения:
1) ЦФ м. б. записана как сумма n от одной переменной:  – сепарабельная ЦФ. Решением задач с такой ЦФ занимается сепарабельное программ-е.
2) ЦФ можно представить как сумму линейной и квадратичной формы, т. е. – сепарабельная ЦФ. Решением задач с такой ЦФ занимается сепарабельное программ-е.
2) ЦФ можно представить как сумму линейной и квадратичной формы, т. е.
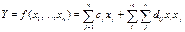 - квадратичная и, след-но, раздел нелинейного программ-я назыв-ся квадратичным программированием.
Задачи с нелин-ми огр-ми явл-ся более сложными для анализа. Общее решение для таких задач удается найти обычно лишь в тех случаях, когда ограничения могут быть представлены в виде сепарабельной функции: - квадратичная и, след-но, раздел нелинейного программ-я назыв-ся квадратичным программированием.
Задачи с нелин-ми огр-ми явл-ся более сложными для анализа. Общее решение для таких задач удается найти обычно лишь в тех случаях, когда ограничения могут быть представлены в виде сепарабельной функции: 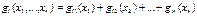 . И даже в случае предст-я огр-й виде возможно получить реш-е лишь в том случае, когда на функцию gij и ЦФ наложены жесткие доп-ые огр-я. В классе нел-х задач выделяют так называемые классические задачи оптимизации.
Пусть сущ-ет общая задача НЛП. Предположим, что среди огр-ий нет нерав-в, нет условий неотр-сти и дискретности эл-в, m< n и ф-ии g(x1, …, xn) и f(x1, …, xn) – непр-ны и имеют частные произв-ые по крайней мере 2-го порядка. В этом случае нелинейная задача м. б. представлена в виде:
найти экстремум ЦФ . И даже в случае предст-я огр-й виде возможно получить реш-е лишь в том случае, когда на функцию gij и ЦФ наложены жесткие доп-ые огр-я. В классе нел-х задач выделяют так называемые классические задачи оптимизации.
Пусть сущ-ет общая задача НЛП. Предположим, что среди огр-ий нет нерав-в, нет условий неотр-сти и дискретности эл-в, m< n и ф-ии g(x1, …, xn) и f(x1, …, xn) – непр-ны и имеют частные произв-ые по крайней мере 2-го порядка. В этом случае нелинейная задача м. б. представлена в виде:
найти экстремум ЦФ 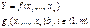 – это классическая задача оптимизации.
Такие задачи могут быть решены ср-ми класс-х методов на основе исп-я дифференциального исчисления. Но на практике, в силу большой размерности задач чаще исп-ют приближенные методы вычислений, разрабатывая для каждого типа задач конкретные вычислительные приемы.
Особый класс нелин-х задач сост-ют задачи, в кот-х на все переем-ые наложено требование целочисл-сти. Такие задачи целочисленные, а программирование целочисленное.
Найти экстремум: – это классическая задача оптимизации.
Такие задачи могут быть решены ср-ми класс-х методов на основе исп-я дифференциального исчисления. Но на практике, в силу большой размерности задач чаще исп-ют приближенные методы вычислений, разрабатывая для каждого типа задач конкретные вычислительные приемы.
Особый класс нелин-х задач сост-ют задачи, в кот-х на все переем-ые наложено требование целочисл-сти. Такие задачи целочисленные, а программирование целочисленное.
Найти экстремум: 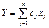 При
При 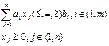 Все или некоторые переменные xj -целые.
Все или некоторые переменные xj -целые.
|
2. Трудности, порождаемые нелинейностями. Выделим осн-ые особенности задач ЛП: а) Мн-во допустимых решений [x1, …, xn] явлся выпуклым. Это выпуклое мнво конечное число вершин, кот-ое обычно называют экстремумами (крайними) точками. б) Мн-во всех точек [x1, …, xn], в кот-х ЦФ принимает заданное зн-е есть гиперплоскость. Кроме того, гиперплоскости, соответствующие различным значениям ЦФ параллельны. в) Локальный экстремум явл-ся одновр-но и глобальным на всем мн-ве допуст-х зн-й. Т. е. не существует локального экстремума ЦФ, отличного от глобального. г) Если оптимальное реш-е ЦФ ограничено, то по крайней мере одна крайняя точка явл-ся оптим-м реш-м. Кроме того, начав с произвольной крайней точки, за конечное число шагов можно достичь оптимальной крайней точки. В нелинейных задачах все или некоторые особенности отсутствуют. Рассмотрим на примерах: 1. Линейная задача. (рисунок начертить ко всем! )
При Решение: x1* = 4/3; x2* = 14/3; Y* = 10. 2. Задача НЛП, в которой меняется лишь ЦФ:
В итоге получим: x1* = 2, 5; x2* = 3, 5; Y* = 15. Получили решение не в крайней точке! Из этого следует, что не сущ-ет вычислительной процедуры для задач такого типа, которая ограничивалась бы перебором только вершин множества допустимых решений. 3. Ограничения те же. Решение – центр эллипса: x1* = 2; x2* = 3; Y* = 0. Решение лежит внутри области, а не на границе. В рассмотренном случае min ЦФ при наличии огр-й и условий неотр-сти тот же, что и без них. След-но, в этом случае говорят, что ограничения несущественны. 4. При ограничениях:
Мы имеем два экстремума: локальный в B и глобальный в Q. Оба экстремума лежат в вершинах мн-ва доп-х реш-й. Т. е. двигаясь от одной вершины к другой, в соответствии с симплекс методом мы не получим решение задачи. 5. Пусть огр-я имеют вид:
ЦФ: Если задача сод-т нелин-е огр-я, то критерий невыпуклости области доп-х реш-й идет в тартарары. Кроме того она может состоять из нескольких взаимонесвязных областей. Если это множество невыпукло, то может существовать отличный от глобального локальный оптимум даже при линейной функции. Для задач НЛП большинство вычислх методов позволяет найти именно точку локго оптимума и в общем случае сразу не позволяет уст-ть совпадает ли она с точкой глоб-го оптимума. Единственный вычислительный метод, приводящий к глобальному оптимуму независимо от числа локальных это метод динамического программирования. 6.
Если х1, 2 не целочисленные, то х1 = 0; х2 = 0, 75; Y = 1, 75. Если целочисленные, то x1* = 1; x2* = 1; Y* = 25. В общем случае для целочх задач решение не совпадает с решением задач ЛП округленного до ближайших целых. |
3. Квадратичное программирование Постановка задачи и предварительные замечания. В общем виде задача КП имеет следующий вид:
где xai – дополняющие переменные, кот-е превращают огр-я в равенства. Для большинства методов решения НЛ задач принято считать, что все bi ³ 0. При сделанных допущениях относительно bi для практических задач можно получить три варианта решения: - решение может находиться внутри области ограничения; - решение может находиться на границе области ограничения; - решение может находиться в вершине области ограничения. Поскольку заранее неизвестно, какой вид реш-я будет получен, при разработке всех методов решения задач КП, в отличие от линейных задач, учитываются и небазисные решения. Преобразование квадратичной целевой функции.
(4) Y = (0 + 1× x1 +5/2× x2 + 0× x3)× 1 + +(1 - 1/4× x1 +1/2× x2 -3/2× x3)× x1+ +(5/2+1/2× x1 - 4× x2 + 0× x3)× x2+ +( 0 -3/2× x1 + 0× x2 + 0× x3)× x3 Возьмём частные производные: (5) dY/dx1 = 2 -1/2× x1 + 1× x2 - 3× x3 = 2× ( 1 -1/4× x1 +1/2× x2 - 3/2× x3); dY/dx2 = 5 +1× x1 - 8× x2 = 2× (5/2+1/2× x1 - 4× x2); dY/dx3= -3× x1 = 2× (-3/2× x1). Анализируя (4), видим, что в скобках при переменных находятся соответствующие частные производные. А они-то явл-ся лин-ми ф-ми (! ) Данное обст-во позволяет строить симплексную процедуру для решения задач КП. В процессе исп-я квадратичного симплексного алг-ма требуется введение в базис новых переем-х, кот-е связаны с выражениями в скобках в соотношении (4). По аналогии с задачами ЛП эти переменные принято называть свободными. Введём свободные переменные, связанные с выражением в скобках при x1.
Коэф-т при U равен коэф-ту при x1, взятому с противоп-м знаком. Тогда Исключим переменную x1 из (4). Получим: (**) Y = ( 4 + 0× U +9/2× x2 + 6× x3)× 1 + + ( 0-1/4× U + 0× x2 - 0× x3)× U+ + (9/2+ 0× U - 3× x2 - 3× x3)× x2+ + ( 6 + 0× U - 3× x2 + 9× x3)× x3 Полученная форма (**) так же является симметричной. Подобное упрощение всегда возникает, если свободные переменные вводить в соответствии с выражением (6).
| ||
4. Квадратичный симплекс метод.
Квадратичный симплексный алгоритм.
1) Принять  , , 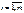 в качестве исходного базисного решения.
2) Опр-ть направление локального улучшения на основе текущего. Прекратить решение, если возможностей улучшения не имеется. Иначе – найти оптимальную длину шага для выбранного направления и перейти к шагу 3.
3) Вычислить новое решение и перейти к шагу 2.
На нач-м этапе имеется с-ма лин-х огр-й, кот-ая на последующих итерациях дополняется новыми огр-ми. В начальный момент кол-во огр-й равно m, в дальнейшем оно увеличивается, но всегда остаётся меньше, чем (m+n).
Базисные решения включают как переменные xj, заданные в исх-й задаче, так и доп-ные переем-ые xai; небазисные перем-ые включают перем-ые xjи xai, а так же свободные переменные, введённые на предыдущей итерации.
Этапы алгоритма:
1) Введите в решение любую свободную переменную, если соотв-щая ей частная производная ЦФ не равна 0.
2) Если все такие производные, соответствующие свободным переменным, равны 0, то выберите для введения в решение такую переменную xj или xai, при которой соответствующая частная производная ЦФ явл-ся полож-ой и наиб-ей по зн-ю.
3) Прекратите расчёты, если все частные произв-ые для свободных переменных равны 0, а для других, небазисных переменных, неположительные.
Вычисление оптимальной длины шага для вводимой переменной определяет содержание второго шага симплексного алгоритма.
При этом анализируется два фактора:
1. Проверка возможности максимального улучшения ц. ф.
2. Обеспечение допуст-сти реш-я, т. е. проверка огр-й задачи.
Свойства:
1) Как и в симпл-м лин-м алг-ме улучшение обуславливается введением в реш-е на каждой итерации только одной небазисной переменной.
2) Как и в симплексном лин-м алг-ме зн-е вводимой переменной не может превысить уровня, при кот-м зн-е любой переменной, входящей в текущий базис уменьшается до 0.
3) Если значение ЦФ при движении в выбранном направлении достигает максимума раньше того момента, когда хотя бы одна базисная переменная уменьшается до 0, к исходной системе ограничений добавляется дополнительное ограничение.
4) Выражение входящее в доп-ое огр-е пропорц-но частной производной ЦФ по вводимой переменной, а следовательно является линейным, т. к. ЦФ квадратичная.
5) Такие огр-я исп-ют как вспомогательные, чтобы определить опт-ую длину шага в выбранном напр-ии. В дальнейшем они могут расширить базис, в связи с чем в оптимальном решении полож-ое зн-е могут иметь более чем m переменных.
Сходимость квадратичного симплексного алгоритма.
После введения вспомог-х переем-х в огр-я, задача КП в матричной форме выглядит следующим образом: в качестве исходного базисного решения.
2) Опр-ть направление локального улучшения на основе текущего. Прекратить решение, если возможностей улучшения не имеется. Иначе – найти оптимальную длину шага для выбранного направления и перейти к шагу 3.
3) Вычислить новое решение и перейти к шагу 2.
На нач-м этапе имеется с-ма лин-х огр-й, кот-ая на последующих итерациях дополняется новыми огр-ми. В начальный момент кол-во огр-й равно m, в дальнейшем оно увеличивается, но всегда остаётся меньше, чем (m+n).
Базисные решения включают как переменные xj, заданные в исх-й задаче, так и доп-ные переем-ые xai; небазисные перем-ые включают перем-ые xjи xai, а так же свободные переменные, введённые на предыдущей итерации.
Этапы алгоритма:
1) Введите в решение любую свободную переменную, если соотв-щая ей частная производная ЦФ не равна 0.
2) Если все такие производные, соответствующие свободным переменным, равны 0, то выберите для введения в решение такую переменную xj или xai, при которой соответствующая частная производная ЦФ явл-ся полож-ой и наиб-ей по зн-ю.
3) Прекратите расчёты, если все частные произв-ые для свободных переменных равны 0, а для других, небазисных переменных, неположительные.
Вычисление оптимальной длины шага для вводимой переменной определяет содержание второго шага симплексного алгоритма.
При этом анализируется два фактора:
1. Проверка возможности максимального улучшения ц. ф.
2. Обеспечение допуст-сти реш-я, т. е. проверка огр-й задачи.
Свойства:
1) Как и в симпл-м лин-м алг-ме улучшение обуславливается введением в реш-е на каждой итерации только одной небазисной переменной.
2) Как и в симплексном лин-м алг-ме зн-е вводимой переменной не может превысить уровня, при кот-м зн-е любой переменной, входящей в текущий базис уменьшается до 0.
3) Если значение ЦФ при движении в выбранном направлении достигает максимума раньше того момента, когда хотя бы одна базисная переменная уменьшается до 0, к исходной системе ограничений добавляется дополнительное ограничение.
4) Выражение входящее в доп-ое огр-е пропорц-но частной производной ЦФ по вводимой переменной, а следовательно является линейным, т. к. ЦФ квадратичная.
5) Такие огр-я исп-ют как вспомогательные, чтобы определить опт-ую длину шага в выбранном напр-ии. В дальнейшем они могут расширить базис, в связи с чем в оптимальном решении полож-ое зн-е могут иметь более чем m переменных.
Сходимость квадратичного симплексного алгоритма.
После введения вспомог-х переем-х в огр-я, задача КП в матричной форме выглядит следующим образом:
 D - симметрическая. При этом рассматривается задача максимизации, т. к. задача минимизации может быть сведена к ней изменением знака ЦФ.
D - симметрическая. При этом рассматривается задача максимизации, т. к. задача минимизации может быть сведена к ней изменением знака ЦФ.
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
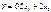


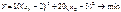
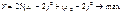
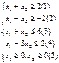
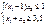
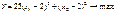
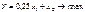
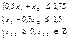
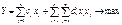 (1)
(1) 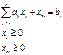 (2)
(2)
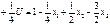 (6)
(6)