
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Статистический ряд частот и относительных частот n=100
Федеральное агентство железнодорожного транспорта
Иркутский государственный университет путей сообщения
РГР на тему: «Статистическая выборка данных»
Вариант № 5
Выполнила: студентка 2 курса
Гр. ПС-10-1
Дашидондокова Л.
Проверила: ст. преподаватель
Кудряшева Л. А.
Иркутск 2012
Статистический ряд частот и относительных частот n=100
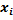
| |||||||||||||||||||||
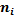
| |||||||||||||||||||||
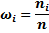
| 0. 02 | 0. 01 | 0. 01 | 0. 01 | 0. 02 | 0. 02 | 0. 02 | 0. 01 | 0. 02 | 0. 01 | 0. 03 | 0. 03 | 0. 01 | 0. 02 | 0. 05 | 0. 05 | 0. 06 | 0. 02 | 0. 06 | 0. 06 | 0. 04 |
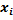
| |||||||||||||||||||||
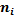
| |||||||||||||||||||||
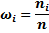
| 0. 02 | 0. 01 | 0. 05 | 0. 06 | 0. 02 | 0. 02 | 0. 03 | 0. 04 | 0. 01 | 0. 02 | 0. 01 | 0. 02 | 0. 02 | 0. 01 | 0. 01 | 0. 01 | 0. 02 | 0. 01 | 0. 01 | 0. 01 | 0. 01 |
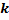
| [8; 13) | [13; 18) | [18; 23) | [23; 28) | [28; 33) | [33; 38) | [38; 43) | [43; 48) | [48; 53) |
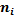
| |||||||||
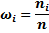
| 0. 05 | 0. 07 | 0. 1 | 0. 18 | 0. 2 | 0. 16 | 0. 11 | 0. 07 | 0. 06 |
Эмпирическая функция распределения
0, x< 8
0. 05, 8< x< 13
0. 12, 13< x< 18
0. 22, 18< x< 23
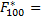 0. 4, 23< x< 28
0. 4, 23< x< 28
0. 6, 28< x< 33
0. 76, 33< x< 38
0. 87, 38< x< 43
0. 94, 43< x< 48
1, 48< x< 53
График эмпирической функции распределения
Гистограмма
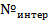
| Интервал | 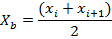
| Частота
Вариант
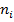
| 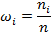
| 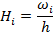
| 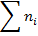
| 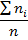
| 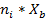
| 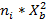
|
| [8; 13) | 10. 5 | 0. 05 | 0. 01 | 0. 05 | 52. 5 | 551. 25 | |||
| [13; 18) | 15. 5 | 0. 07 | 0. 014 | 0. 12 | 108. 5 | 1681. 75 | |||
| [18; 23) | 20. 5 | 0. 1 | 0. 02 | 0. 22 | 4202. 5 | ||||
| [23; 28) | 25. 5 | 0. 18 | 0. 036 | 0. 4 | 11704. 5 | ||||
| [28; 33) | 30. 5 | 0. 2 | 0. 04 | 0. 6 | |||||
| [33; 38) | 35. 5 | 0. 16 | 0. 032 | 0. 76 | |||||
| [38; 43) | 40. 5 | 0. 11 | 0. 022 | 0. 87 | 445. 5 | 18042. 75 | |||
| [43; 48) | 45. 5 | 0. 07 | 0. 014 | 0. 94 | 318. 5 | 14491. 75 | |||
| [48; 53) | 50. 5 | 0. 06 | 0. 012 | 0. 1 | 15301. 5 |
=3070 =104745
Из данной гистограммы делаем вывод, что данный статистический ряд распределен по нормальному закону.

 i
i 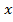 i
i 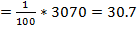
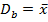 b2 –
b2 – 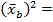
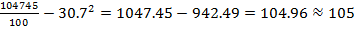
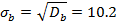
 2
2 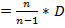 b
b 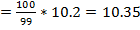
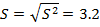
Доверительный интервал
Для математического ожидания
Предположим, что данная выборка распределена по нормальному закону (условие нормального распределения дано в задании).
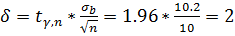
1)Для надежности 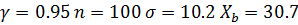
Т. к. мат. ожидание неизвестно
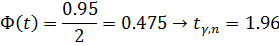
Значение математического ожидания 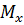 c надежностью
c надежностью 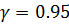 попадает в интервал
попадает в интервал 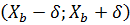

То же самое для надежности 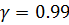
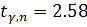
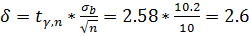
Интервал 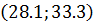
Для среднеквадратического отклонения
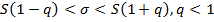
С надежностью 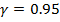
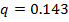
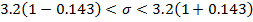
Значение среднеквадратического отклонения с 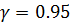 попадает в интервал (2. 74; 3. 65)
попадает в интервал (2. 74; 3. 65)
Аналогично находим интервал для среднеквадратического отклонения с надежностью 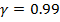
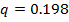
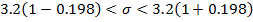
интервал (2. 5; 3. 5)
Ранее мы выдвинули гипотезу о законе распределения.
Проверим данную гипотезу с помощью критерия Пирсона χ 2
k=2
Найдем оценку параметра предполагаемого распределения.
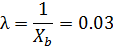
Найдем вероятности попадания Х в каждый из интервалов:
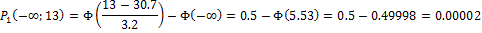
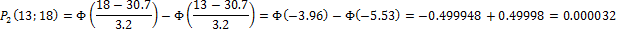
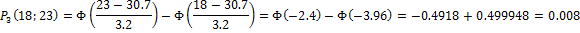

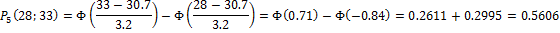
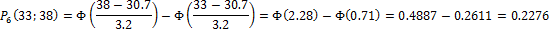

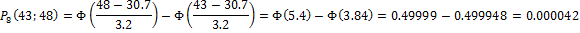
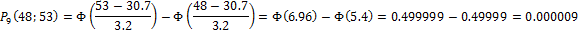
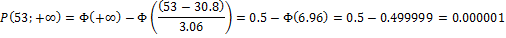
Теперь найдем теоретические частоты:
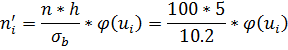
Составляем расчетную таблицу:
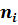
| 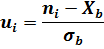
| 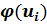
| 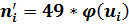
|
| -1, 83333 | 0. 0748 | 3, 6652 | |
| -2, 02941 | 0. 0519 | 2, 5431 | |
| -1, 2451 | 0. 1849 | 9, 0601 | |
| -1, 04902 | 0. 2323 | 11, 3827 | |
| -1, 44118 | 0. 1415 | 6, 9335 | |
| -1, 93137 | 0. 0620 | 3, 038 | |
| -2, 32353 | 0. 0270 | 1, 323 | |
| -2, 42157 | 0. 0213 | 1, 0437 |
| № | 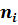
| 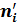
| 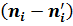
| 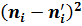
| 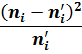
|
| 3, 6652 | 8, 3348 | 69, 46889 | 18, 95364 | ||
| 2, 5431 | 7, 4569 | 55, 60536 | 21, 86519 | ||
| 9, 0601 | 8, 9399 | 79, 92181 | 8, 821295 | ||
| 11, 3827 | 8, 6173 | 74, 25786 | 6, 523747 | ||
| 6, 9335 | 9, 0665 | 82, 20142 | 11, 85569 | ||
| 3, 038 | 7, 962 | 63, 39344 | 20, 86683 | ||
| 1, 323 | 5, 677 | 32, 22833 | 24, 36004 | ||
| 1, 0437 | 4, 9563 | 24, 56491 | 23, 53637 | ||
| Σ | 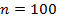
| χ 2набл= 136, 7828 |
При уровне значимости α =0, 05 χ 2кр=6, 0 α =0, 01 χ 2кр=9. 2
Так как χ 2набл > χ 2кр – мы отвергаем гипотезу о распределении X по нормальному распределению.
Теперь найдем теоретические частоты:
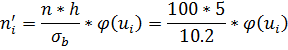
Составляем расчетную таблицу:
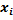
| 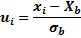
| 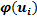
| 
| 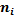
| 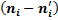
| 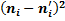
| 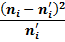
|
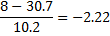
| 0. 0339 | 1, 6611 | 0, 3389 | 0, 114853 | 0, 069143 | ||
| -2. 12 | 0. 0422 | 2, 0678 | -1, 0678 | 1, 140197 | 0, 551406 | ||
| -2. 02 | 0. 0519 | 2, 5431 | -1, 5431 | 2, 381158 | 0, 936321 | ||
| -1. 83 | 0. 0748 | 3, 6652 | -2, 6652 | 7, 103291 | 1, 938036 | ||
| -1. 63 | 0. 1057 | 5, 1793 | -3, 1793 | 10, 10795 | 1, 951605 | ||
| -1. 54 | 0. 1219 | 5, 9731 | -3, 9731 | 15, 78552 | 2, 642769 | ||
| -1. 44 | 0. 1415 | 6, 9335 | -4, 9335 | 24, 33942 | 3, 510409 | ||
| -1. 34 | 0. 1626 | 7, 9674 | -6, 9674 | 48, 54466 | 6, 092911 | ||
| -1. 24 | 0. 1849 | 9, 0601 | -7, 0601 | 49, 84501 | 5, 501596 | ||
| -1. 14 | 0. 2083 | 10, 2067 | -9, 2067 | 84, 76332 | 8, 304675 | ||
| -1. 05 | 0. 2299 | 11, 2651 | -8, 2651 | 68, 31188 | 6, 064028 | ||
| -0. 95 | 0. 2541 | 12, 4509 | -9, 4509 | 89, 31951 | 7, 173739 | ||
| -0. 85 | 0. 2780 | 13, 622 | -12, 622 | 159, 3149 | 11, 69541 | ||
| -0. 65 | 0. 3230 | 15, 827 | -13, 827 | 191, 1859 | 12, 07973 | ||
| -0. 55 | 0. 3429 | 16, 8021 | -11, 8021 | 139, 2896 | 8, 290009 | ||
| -0. 46 | 0. 3589 | 17, 5861 | -12, 5861 | 158, 4099 | 9, 007677 | ||
| -0. 36 | 0. 3739 | 18, 3211 | -12, 3211 | 151, 8095 | 8, 286048 | ||
| -0. 26 | 0. 3857 | 18, 8993 | -16, 8993 | 285, 5863 | 15, 11095 | ||
| -0. 16 | 0. 3939 | 19, 3011 | -13, 3011 | 176, 9193 | 9, 166279 | ||
| -0. 06 | 0. 3982 | 19, 5118 | -13, 5118 | 182, 5687 | 9, 356837 | ||
| 0. 02 | 0. 3989 | 19, 5461 | -15, 5461 | 241, 6812 | 12, 36468 | ||
| 0. 12 | 0. 3961 | 19, 4089 | -17, 4089 | 303, 0698 | 15, 61499 | ||
| 0. 22 | 0. 3894 | 19, 0806 | -18, 0806 | 326, 9081 | 17, 13301 | ||
| 0. 32 | 0. 3790 | 18, 571 | -13, 571 | 184, 172 | 9, 917185 | ||
| 0. 42 | 0. 3652 | 17, 8948 | -11, 8948 | 141, 4863 | 7, 906558 | ||
| 0. 51 | 0. 3503 | 17, 1647 | -15, 1647 | 229, 9681 | 13, 39774 | ||
| 0. 61 | 0. 3312 | 16, 2288 | -14, 2288 | 202, 4587 | 12, 47528 | ||
| 0. 71 | 0. 3101 | 15, 1949 | -12, 1949 | 148, 7156 | 9, 787204 | ||
| 0. 81 | 0. 2874 | 14, 0826 | -10, 0826 | 101, 6588 | 7, 218754 | ||
| 0. 91 | 0. 2637 | 12, 9213 | -11, 9213 | 142, 1174 | 10, 99869 | ||
| 0. 2420 | 11, 858 | -9, 858 | 97, 18016 | 8, 195325 | |||
| 1. 1 | 0. 2179 | 10, 6771 | -9, 6771 | 93, 64626 | 8, 770758 | ||
| 1. 2 | 0. 1942 | 9, 5158 | -7, 5158 | 56, 48725 | 5, 936154 | ||
| 1. 3 | 0. 1714 | 8, 3986 | -6, 3986 | 40, 94208 | 4, 87487 | ||
| 1. 4 | 0. 1497 | 7, 3353 | -6, 3353 | 40, 13603 | 5, 471627 | ||
| 1. 5 | 0. 1295 | 6, 3455 | -5, 3455 | 28, 57437 | 4, 503092 | ||
| 1. 59 | 0. 1127 | 5, 5223 | -4, 5223 | 20, 4512 | 3, 703384 | ||
| 1. 69 | 0. 0957 | 4, 6893 | -2, 6893 | 7, 232334 | 1, 542306 | ||
| 1. 79 | 0. 0804 | 3, 9396 | -2, 9396 | 8, 641248 | 2, 193433 | ||
| 1. 89 | 0. 0669 | 3, 2781 | -2, 2781 | 5, 18974 | 1, 583155 | ||
| 1. 99 | 0. 0551 | 2, 6999 | -1, 6999 | 2, 88966 | 1, 070284 | ||
| 2. 08 | 0. 0459 | 2, 2491 | -1, 2491 | 1, 560251 | 0, 693722 |
=293. 0818
При уровне значимости α =0, 05 χ 2кр=6, 0 α =0, 01 χ 2кр=9. 2
Так как χ 2набл > χ 2кр – мы отвергаем гипотезу о распределении X по нормальному распределению.
Теперь найдем теоретические частоты:
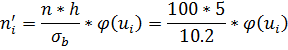
Составляем расчетную таблицу:
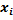
| 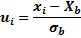
| 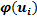
| 
|
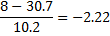
| 0. 0339 | 1, 6611 | |
| -2. 12 | 0. 0422 | 2, 0678 | |
| -2. 02 | 0. 0519 | 2, 5431 | |
| -1. 83 | 0. 0748 | 3, 6652 | |
| -1. 63 | 0. 1057 | 5, 1793 | |
| -1. 54 | 0. 1219 | 5, 9731 | |
| -1. 44 | 0. 1415 | 6, 9335 | |
| -1. 34 | 0. 1626 | 7, 9674 | |
| -1. 24 | 0. 1849 | 9, 0601 | |
| -1. 14 | 0. 2083 | 10, 2067 | |
| -1. 05 | 0. 2299 | 11, 2651 | |
| -0. 95 | 0. 2541 | 12, 4509 | |
| -0. 85 | 0. 2780 | 13, 622 | |
| -0. 65 | 0. 3230 | 15, 827 | |
| -0. 55 | 0. 3429 | 16, 8021 | |
| -0. 46 | 0. 3589 | 17, 5861 | |
| -0. 36 | 0. 3739 | 18, 3211 | |
| -0. 26 | 0. 3857 | 18, 8993 | |
| -0. 16 | 0. 3939 | 19, 3011 | |
| -0. 06 | 0. 3982 | 19, 5118 | |
| 0. 02 | 0. 3989 | 19, 5461 | |
| 0. 12 | 0. 3961 | 19, 4089 | |
| 0. 22 | 0. 3894 | 19, 0806 | |
| 0. 32 | 0. 3790 | 18, 571 | |
| 0. 42 | 0. 3652 | 17, 8948 | |
| 0. 51 | 0. 3503 | 17, 1647 | |
| 0. 61 | 0. 3312 | 16, 2288 | |
| 0. 71 | 0. 3101 | 15, 1949 | |
| 0. 81 | 0. 2874 | 14, 0826 | |
| 0. 91 | 0. 2637 | 12, 9213 | |
| 0. 2420 | 11, 858 | ||
| 1. 1 | 0. 2179 | 10, 6771 | |
| 1. 2 | 0. 1942 | 9, 5158 | |
| 1. 3 | 0. 1714 | 8, 3986 | |
| 1. 4 | 0. 1497 | 7, 3353 | |
| 1. 5 | 0. 1295 | 6, 3455 | |
| 1. 59 | 0. 1127 | 5, 5223 | |
| 1. 69 | 0. 0957 | 4, 6893 | |
| 1. 79 | 0. 0804 | 3, 9396 | |
| 1. 89 | 0. 0669 | 3, 2781 | |
| 1. 99 | 0. 0551 | 2, 6999 | |
| 2. 08 | 0. 0459 | 2, 2491 |
| № | 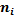
| 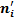
| 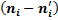
| 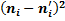
| 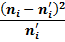
|
| 35. 9905 | -23, 9905 | 575, 5441 | 15, 99156 | ||
| 56. 6048 | -46, 6048 | 2172, 007 | 38, 37143 | ||
| 68. 5363 | -50, 5363 | 2553, 918 | 37, 26372 | ||
| 96. 6672 | -76, 6672 | 5877, 86 | 60, 80511 | ||
| 88. 9399 | -72, 9399 | 5320, 229 | 59, 81825 | ||
| 64. 7339 | -53, 7339 | 2887, 332 | 44, 60309 | ||
| 37. 1175 | -30, 1175 | 907, 0638 | 24, 43763 | ||
| 16. 856 | -10, 856 | 117, 8527 | 6, 991738 | ||
| Σ | 
| χ 2набл= 288, 2825 |
При уровне значимости α =0, 05 χ 2кр=6, 0 α =0, 01 χ 2кр=9. 2
Так как χ 2набл > χ 2кр – мы отвергаем гипотезу о распределении X по нормальному распределению.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|