«МЕТОДЫ ЗАЩИТЫ ИНФОРМАЦИИ В ПЛАТЕЖНЫХ И БАНКОВСКИХ СИСТЕМАХ. КРИПТОГРАФИЧЕСКИЕ МЕТОДЫ ЗАЩИТЫ»

Министерство образования и науки РФ

ФГБОУ ВПО «Дагестанский Государственный Технический Университет»

ДОКЛАД

на тему:

«МЕТОДЫ ЗАЩИТЫ ИНФОРМАЦИИ В ПЛАТЕЖНЫХ И БАНКОВСКИХ СИСТЕМАХ. КРИПТОГРАФИЧЕСКИЕ МЕТОДЫ ЗАЩИТЫ»

Выполнил: ст-т гр. У 051

Гамзатов М.

Принял:

Магомедов Ш. Г.

Махачкала 2014

Современная криптография включает в себя следующие основные разделы:

· криптосистемы с секретным ключом (классическая криптография);

· криптосистемы с открытым ключом;

· криптографические протоколы.

1. Оценка надежности криптоалгоритмов

Все современные шифры базируются на принципе Кирхгофа [1], согласно которому секретность шифра обеспечивается секретностью ключа, а не секретностью алгоритма шифрования. В некоторых ситуациях нет никаких причин делать общедоступным описание сути криптосистемы. Сохраняя такую информацию в тайне, можно дополнительно повысить надежность шифра. Однако полагаться на секретность этой информации не следует, так как рано или поздно она будет скомпрометирована. При создании или при анализе стойкости криптосистем не следует недооценивать возможностей противника.

Методы оценки качества криптоалгоритмов, используемые на практике:

· Всевозможные попытки их вскрытия. В этом случае многое зависит от квалификации, опыта, интуиции криптоаналитиков и от правильной оценки возможностей противника.

· Анализ сложности алгоритмов дешифрования. Оценку стойкости шифра заменяют оценкой минимальной сложности алгоритма его вскрытия.

· Оценка статической безопасности шифра. Должна отсутствовать статическая зависимость между входной и выходной последовательностью.

2. Классификация методов шифрования информации

Основные объекты изучения классической криптографии показаны на рис. 1, где А – законный пользователь, W – противник или криптоаналитик.

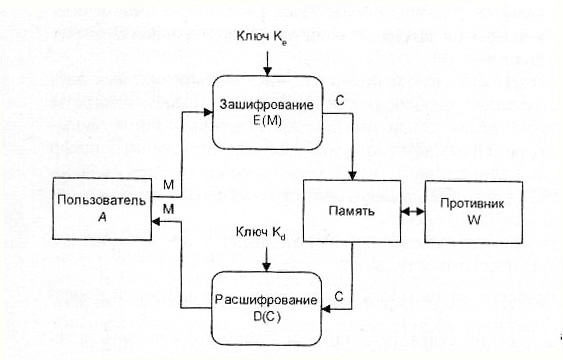
Рис. 1. Криптографическая защита информации

Процедуры зашифрования Е (encryption) и расшифрования D (decryption) можно представить в следующем виде:

C = E(M) = K_e{M},

M = D(C) = K_d{C},

где M (message) и C (ciphertext) – открытый и зашифрованный тексты, K_e и K_d – ключи зашифрования и расшифрования.

Различают два типа алгоритмов шифрования – симметричные (с секретным ключом) и асимметричные (с открытым ключом). В первом случае обычно ключ расшифрования совпадает с ключом зашифрования, т. е

K_e = K_d =K,

либо знание ключа зашифрования позволяет легко вычислить ключ расшифрования. В асимметричных алгоритмах такая возможность отсутствует: для зашифрования и расшифрования используются разные ключи, причем знание одного из них не дает практической возможности определить другой. Поэтому, если получатель А информации сохраняет в секрете ключ расшифрования K_dA = SK_A, ключ зашифрования K_eA = PK_A может быть сделан общедоступным (SK – secret key, PK – public key).

В процессе шифрования информация делится на порции величиной от одного до сотен бит. Как правило, поточные шифры оперируют с битами открытого и закрытого текстов, а блочные – с блоками фиксированной длины. Главное отличие между этими двумя методами заключается в том, что в блочных шифрах для шифрования всех порций используется один и тот же ключ, а в поточных – для каждой порции используется свой ключ той же размерности.

3. Абсолютно стойкий шифр. Гаммирование.

Простейшей и в то же время наиболее надежной из всех систем шифрования является так называемая схема однократного использования. Формируется m-разрядная случайная двоичная последовательность – ключ шифра, известный отправителю и получателю сообщения. Отправитель производит побитовое сложение по модулю 2 ключа и m-разрядной двоичной последовательности, соответствующей пересылаемому сообщению:

C_i = K_i (+) M_i,

где M_i, K_i и C_i – очередной i-й бит соответственно исходного сообщения, ключа и зашифрованного сообщения, m – число битов открытого текста. Процесс расшифрования сводится к повторной генерации ключевой последовательности и наложению ее на зашифрованные данные. Уравнение расшифрования имеет вид:

M_i = K_i (+) C_i, i = 1.. m.

К. Шенноном доказано, что, если ключ является фрагментом истинно случайной двоичной последовательности с равномерным законом распределения, причем его длина равна длине исходного сообщения и используется этот ключ только один раз, после чего уничтожается, такой шифр является абсолютно стойким, его невозможно раскрыть, даже если криптоаналитик располагает неограниченным запасом времени и неограниченным набором вычислительных ресурсов. Действительно, противнику известно только зашифрованное сообщение С, при этом все различные ключевые последовательности К возможны и равновероятны, а значит, возможны и любые перемещения М, т. е. криптоалгоритм не дает никакой информации об открытом тексте.

Необходимые и достаточные условия абсолютной стойкости шифра:

· полная случайность ключа;

· равенство длин ключа и открытого текста;

· однократное использование ключа.

Абсолютная стойкость рассмотренной схемы оплачивается слишком большой ценой, она чрезвычайно дорогая и непрактичная. Основной ее недостаток – это равенство объема ключевой информации и суммарного объема передаваемых сообщений. Применение схемы оправдано лишь в нечасто используемых каналах связи для шифрования исключительно важных сообщений.

Таким образом, построить эффективный криптоалгоритм можно, лишь отказавшись от абсолютной стойкости. Возникает задача разработки такого теоретически нестойкого шифра, для вскрытия которого противнику потребовалось бы выполнить такое число операций, которое неосуществимо на современных и ожидаемых в ближайшей перспективе вычислительных средствах за разумное время. В первую очередь следует иметь схему, которая использует ключ небольшой разрядности, который в дальнейшем выполняет функцию «зародыша», порождающего значительно более длинную ключевую последовательность.

Данный результат может быть достигнут при использовании гаммирования. Гаммированием называют процедуру наложения на входную информационную последовательность гаммы шифра, т. е. последовательности с выходов генератора псевдослучайных последовательностей (ПСП) [1]. Последовательность называется псевдослучайной, если по своим статистическим свойствам она неотличима от истинно случайной последовательности, но в отличие от последней является детерминированной, т. е. знание алгоритма ее формирования дает возможность ее повторения необходимое число раз. Если символы входной информационной последовательности и гаммы представлены в двоичном виде, наложение чаще всего реализуется с помощью операции поразрядного сложения по модулю два. Надежность шифрования методом гаммирования определяется качеством генератора гаммы.

4. Поточные шифры.

Так как поточные шифры, в отличие от блочных, осуществляют поэлементное шифрование потока данных без задержки в криптосистеме, их важнейшим достоинством является высокая скорость преобразования, соизмеримая со скоростью поступления входной информации. Таким образом, обеспечивается шифрование практически в реальном масштабе времени вне зависимости от объема и разрядности потока преобразуемых данных.

В синхронных поточных шифрах гамма формируется независимо от входной последовательности, каждый элемент (бит, символ, байт и т. п. ) которой таким образом шифруется независимо от других элементов. В синхронных поточных шифрах отсутствует эффект размножения ошибок, т. е. число искаженных элементов в расшифрованной последовательности равно числу искаженных элементов зашифрованной последовательности, пришедшей из канала связи. Вставка или выпадение элемента зашифрованной последовательности недопустимы, так как из-за нарушения синхронизации это приведет к неправильному расшифрованию всех последующих элементов.

В самосинхронизирующихся поточных шифрах осуществляется гаммирование с обратной связью – гамма зависит от открытого текста, иначе говоря, результат шифрования каждого элемента зависит не только от позиции этого элемента (как это происходит в случае синхронного поточного шифрования), но и от значения всех предыдущих элементов открытого текста. Свойство самосинхронизации объясняется отсутствием обратной связи на принимающей стороне, в то время как в случае синхронного поточного шифрования схемы за- и расшифрования идентичны.