Вопросы к экзамену для студентов ФЭУ 1 семестр по линейной алгебре.
- Пространства R и
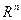 . . - Понятие вектора и линейные операции над векторами.
- Скалярное произведение и его свойства.
- Понятие угла между векторами.
- Условие коллинеарности и ортогональности векторов.
- Линейная зависимость векторов.
- Векторное произведение векторов и его свойства.
- Смешанное произведение векторов и его свойства.
- Евклидово пространство. Неравенство Коши-Буняковского.
- Ортогональный базис. Разложение вектора по ортобазису.
- Виды матриц.
- Действия над матрицами.
- Определители второго и третьего порядков, их свойства.
- Алгебраические дополнения и миноры.
- Определители n-го порядка.
- Вычисление определителя разложением по строке (столбцу).
- Понятие обратной матрицы.
- Построение обратной матрицы элементарными преобразованиями.
- Ранг матрицы.
- Системы двух и трех линейных уравнений. Правило Крамера.
- Система m линейных уравнений с n неизвестными.
- Решение системы линейных уравнений методом Гаусса.
- Решение однородных систем линейных уравнений.
- Решение систем линейных уравнений со ступенчатой матрицей.
- Общее решение систем линейных уравнений. Главные и свободные неизвестные.
- Геометрическая интерпретация систем линейных уравнений в случае двух или трех неизвестных.
- Ненулевые решения однородной системы линейных уравнений.
- Преобразование координат при замене базиса.
- Критерий линейной независимости строк (столбцов).
- Матрица линейного оператора.
- Преобразование матрицы линейного оператора при замене базиса.
- Приведение матриц линейного оператора к диагональному виду.
- Свойства собственных векторов с одинаковыми и различными собственными значениями.
- Формула линейного функционала.
- Матрица билинейной формы.
- Матрица симметричной билинейной формы.
- Преобразование матрицы билинейной формы при замене базиса.
- Единственность симметричной билинейной формы, порождающей квадратичную форму.
- Критерий Сильвестра положительной определенности квадратичной формы.
|

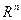 .
.