
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
16. 02. 2022г. Алгебра и начала математического анализа, 11 класс
16. 02. 2022г. Алгебра и начала математического анализа, 11 класс
Урок №22. Правила вычисления первообразной.
Перечень вопросов, рассматриваемых в теме
1) Нахождение первообразной.
2) Определение первообразной, график которой проходит через заданную точку.
3) Решение задач, обратных задаче нахождения закона изменения скорости материальной точки по закону ее движения
Глоссарий по теме
Первообразная. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке Х, если для х 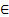 Х выполняется равенство F’ (x) = f(x).
Х выполняется равенство F’ (x) = f(x).
Таблица первообразных:
| Функция f(x) | Первообразная F(x) |
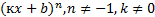
| 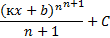
|
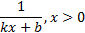
| 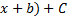
|
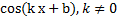
| 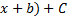
|
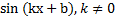
| 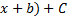
|
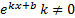
| 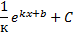
|
Теоретический материал для самостоятельного изучения
Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке Х, если для 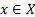 выполняется равенство F’ (x) = f(x).
выполняется равенство F’ (x) = f(x).
1) 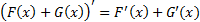
2) 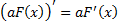
3) 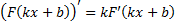
Примеры и разбор решения заданий тренировочного модуля
№1. Для функции y = f(x) найдите множество всех первообразных. Выполните проверку. f(x) = 2sin x + 3x3
Решение:
f(x) = 2sin x + 3x3
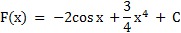
Проверка:
Найдем производную функции F(x).
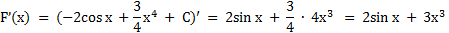
F’(x) = f(x)
Ответ: 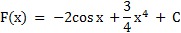
№2. Значение первообразной функции F(x) функции f(x) = 10cosx в точке 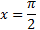 равно -4. Найдите
равно -4. Найдите 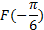 .
.
Решение. Сначала найдем первообразную
F(x) = 10sinx+ C
Затем подставляя значения точки х, найдем число с
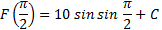
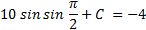
C = -14
Далее получаем уравнение первообразной в этой точке
F(x) = 10sin x – 14
И находим значение первообразной в другой точке
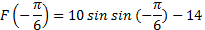
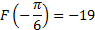
Ответ: -19
№3. По графику первообразной функции y = F(x) определите числовые промежутки, на которых функция y = f(x) имеет отрицательный знак.
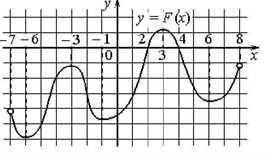
Решение:
Так как F’(x) = f(x)- по определению первообразной, то числовые промежутки, на которых функция f(x) (производная функции F(x)) имеет отрицательный знак – это промежутки убывания функции F(x). Таких промежутков на данном графике 3. Это (-7; -6); (-3; -1); (3; 6)
Ответ: (-7; -6); (-3; -1); (3; 6)
№4. Значение первообразной функции F(x) функции f(x) = 5x3 – 3x2 + 7x – 2 в точке х = 0 равно 5. Найдите F(2).
Решение.
1. Найдем множество всех первообразных для данной функции.
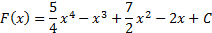
1. Так как в точке х = 0 значение первообразной функции равно 5, то нам необходимо найти такое значение С, для которого выполняется условие F(0) = 5.
Решим уравнение:
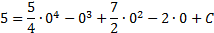
1. Из полученного уравнения находим С = 5.
Следовательно, первообразная для функции f(x) = 5x3 – 3x2 + 7x – 2 при заданном условии F(0) = 5 имеет вид: 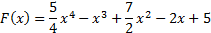
1. Тогда 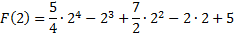
F(2) = 27
Ответ: 27
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|