Задача 49

Задача 49

Определить величину гидравлического радиуса канала трапецеидальной формы, считая, что движение воды в канале равномерное:

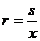, где

s = b*h + m*h² - площадь сечения канала (м²);

- длина смоченного периметра (м).

Исходные данные: ширина канала b=10. 0 (м);

нормальная глубина канала h=3 (м);

откос m=0. 12 (м).

Задача 50

Тепловые потери с 1 пог. метра трубопровода напольной системы отопления вычисляются по формуле О. Е. Власова:

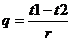, где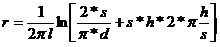

Вычислить тепловые потери q и термическое сопротивление грунта r при следующих исходных данных:

t1=60 (град) - температура трубопровода;

t2=14 (град) - температура поверхности пола;

l=1. 13 (Вт/(м*град)) - коэффициент теплопроводности;

s=0. 2 (м) - шаг трубопроводов;

d=0. 04 (м) - диаметр трубопроводов;

h=0. 16 (м) - глубина заложения трубопроводов.

Задача 51

Определить скорость и расход воды в бетонном канале кругового сечения по формулам:

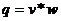, , где 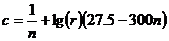- коэффициент Шези;

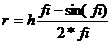- гидравлический радиус потока воды;

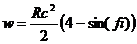- поперечное сечение потока воды.

Исходные данные: радиус сечения Rc=1. 2 (м);

глубина воды h=2. 3 (м);

уклон дна j=0. 6E-4 (м);

коэффициент шероховатости n=0. 02;

угол fi=161 (град).

Задача 52

Вычислить значение функции fi(et) для расчета неравномерного движения воды в трапецеидальном русле по способу проф. Агроскина:

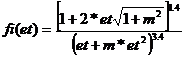, где .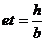

Исходные данные: глубина русла h=4. 0 (м);

ширина русла b=10. 0 (м);

откос m=1. 25 (м).