Теплопроводность через плоскую и цилиндрическую.

73. Классификация процессов теплообмена. Элементарные и сложные формы теплопереноса. Теплообмен — это процесс изменения внутренней энергии без совершения работы над телом или самим телом. Теплообмен всегда происходит в определенном направлении: от тел с более высокой температурой к телам с более низкой. Когда температуры тел выравниваются, теплообмен прекращается. Теплообмен может осуществляться тремя способами: теплопроводностью, конвекцией, излучением. Теплопроводность — явление передачи внутренней энергии от одной части тела к другой или от одного тела к другому при их непосредственном контакте. Наибольшей теплопроводностью обладают металлы — она у них в сотни раз больше, чем у воды. Исключением являются ртуть и свинец, но и здесь теплопроводность в десятки раз больше, чем у воды. Наибольшей теплопроводностью обладают серебро и медь. Теплопроводность у различных веществ различна. Плохой теплопроводностью обладают шерсть, волосы, перья птиц, бумага, пробка и другие пористые тела. Это связано с тем, что между волокнами этих веществ содержится воздух. Самой низкой теплопроводностью обладает вакуум (освобожденное от воздуха пространство). Объясняется это тем, что теплопроводность — это перенос энергии от одной части тела к другой, который происходит при взаимодействии молекул или других частиц. В пространстве, где нет частиц, теплопроводность осуществляться не может. Если возникает необходимость предохранить тело от охлаждения или нагревания, то применяют вещества с малой теплопроводностью. Так, для кастрюль, сковородок ручки из пластмассы. Конвекция — это процесс теплопередачи, осуществляемый путем переноса энергии потоками жидкости или газа. Пример явления конвекции: небольшая бумажная вертушка, поставленная над пламенем свечи или электрической лампочкой, под действием поднимающегося нагретого воздуха начинает вращаться. Это явление можно объяснить таким образом. Воздух, соприкасаясь с теплой лампой, нагревается, расширяется и становится менее плотным, чем окружающий его холодный воздух. Сила Архимеда, действующая на теплый воздух со стороны холодного снизу вверх, больше, чем сила тяжести, которая действует на теплый воздух. В результате нагретый воздух «всплывает», поднимается вверх, а его место занимает холодный воздух. При конвекции энергия переносится самими струями газа или жидкости. Различают два вида конвекции: o естественная (или свободная): возникает в веществе самопроизвольно при его неравномерном нагревании. При такой конвекции нижние слои вещества нагреваются, становятся легче и всплывают, а верхние слои, наоборот, остывают, становятся тяжелее и опускаются вниз, после чего процесс повторяется. o вынужденная: наблюдается при перемешивании жидкости мешалкой, ложкой, насосом и т. д. Для того, чтобы в жидкостях и газах происходила конвекция, необходимо их нагревать снизу. Конвекция в твердых телах происходить не может. Излучение — электромагнитное излучение, испускаемое за счет внутренней энергии веществом, находящимся при определенной температуре. Передача энергии излучением отличается от других видов теплопередачи: она может осуществляться в полном вакууме. Излучают энергию все тела: и сильно нагретые, и слабо, например тело человека, печь, электрическая лампочка и др. Но чем выше температура тела, тем больше энергии передает оно путем излучения. При этом энергия частично поглощается этими телами, а частично отражается. Тела с темной поверхностью лучше поглощают и излучают энергию, чем тела, имеющие светлую поверхность. В то же время тела с темной поверхностью охлаждаются быстрее путем излучения, чем тела со светлой поверхностью. Например, в светлом чайнике горячая вода дольше сохраняет высокую температуру, чем в темном. Теплопередача — физический процесс передачи тепловой энергии от более горячего тела к более холодному либо непосредственно (при контакте), либо через разделяющую (тела или среды) перегородку из какого-либо материала. Когда физические тела одной системы находятся при разной температуре, то происходит передача тепловой энергии, или теплопередача от одного тела к другому до наступления термодинамического равновесия. [Самопроизвольная передача тепла всегда происходит от более горячего тела к более холодному, что является следствием второго закона термодинамики. ] Существуют также различные виды сложного переноса тепла, которые являются сочетанием элементарных видов. Основные из них: · теплоотдача (конвективный теплообмен между потоками жидкости или газа и поверхностью твёрдого тела); · теплопередача (теплообмен от горячей жидкости к холодной через разделяющую их стенку); · конвективно-лучистый перенос тепла (совместный перенос тепла излучением и конвекцией); · [термомагнитная конвекция] [Внутренние источники теплоты - понятие теории теплопередачи, которое описывает процесс производства (реже поглощения) тепловой энергии внутри материальных тел без какого-либо подвода или переноса тепловой энергии извне. К внутренним источникам теплоты относятся: · тепловыделение в электрических нагревателях · тепловыделение при ядерных реакциях · тепловыделение при химических реакциях] Конвективный теплообмен=конвекция+теплопроводностьКондуктивный теплообмен=теплопроводность+излучение Процесс отдачи теплоты между потоком жидкости или газа и твердой пов. тела называют конвективной теплоотдачей. Совокупность всех трех видов называют сложным.

74. Основные термины теории теплообмена: температурное поле, температурный напор, температурный градиент, тепловой поток, плотность теплового потока. Температурное поле - совокупность значений температур во всех точках рассматриваемого пространства в данный момент времени. Математически Т. п. может быть описано уравнением зависимости температур от 3 пространственных координат и от времени (нестационарное трёхмерное Т. п. ). Для установившихся (стационарных) режимов Т. п. от времени не зависит. Во многих случаях может рассматриваться зависимость Т. п. от двух, а иногда от одной координаты. Графически Т. п. изображают посредством изотермических поверхностей, соединяющих все точки поля с одинаковой температурой, а для двухмерного поля — посредством семейства изотерм. Расстояние между изотермами обратно пропорционально Градиенту температуры; при этом скалярному Т. п. соответствует векторное поле градиентов температуры.: t = f (x, у, z, τ ), где функция f описывает связь между температурой t, пространственными координатами х, у, z и временем τ. Температурный напор — разность характерных температур среды и стенки (или границы раздела фаз) или двух сред, между которыми происходит теплообмен. Местный температурный напор — разность температур среды и местной температуры стенки (границы раздела фаз) либо разность температур двух сред в данном сечении теплообменной системы. Средний температурный напор — температурный напор, осреднённый по поверхности теплообмена. Произведение значения температурного напора на коэффициент теплопередачи определяет количество теплоты, передаваемое от одной среды к другой через единицу поверхности нагрева в единицу времени, то есть плотность теплового потока.: Δ t = tг – tx, ; tг и tх – температуры в горячей и в холодной точках. Величина Δ t определяется расстоянием между точками и интенсивностью теплообмена в выбранном направлении. Градиент температурный - величина изменения температуры на единицу длины в направлении распространения теплоты, т. е. по направлению нормали к изотермической поверхности. Выражают в Кельвинах на метр (К/м) или в градусах Цельсия на метр (°С/м).: Величина температурного градиента характеризует максимальную интенсивность изменения температуры в пространстве в окрестностях заданной точки. Это величина векторная, направляют этот вектор в сторону увеличения температуры. Тепловой поток - количество теплоты, переданное через изотермическую поверхность в единицу времени. Размерность Т. п. совпадает с размерностью мощности. Т. п. измеряется в ваттах или ккал/ч (1 вт = 0, 86ккал/ч). : Q = Q*/ τ. Т. п., отнесённый к единице изотермической поверхности, называется плотностью Т. п., удельным Т. п. или тепловой нагрузкой; обозначается обычно q, измеряется в вт/м2 или ккал/(м 2× ч). : q = Q / F. Плотность Т. п. — вектор, любая компонента которого численно равна количеству теплоты, передаваемой в единицу времени через единицу площади, перпендикулярной к направлению взятой компоненты. Плотность теплового потока — отношение теплового потока к площади поверхности, через которую он проходит

75. Основные законы теплообмена: закон Ньютона – Рихмана, закон Фурье, закон Стефана – Больцмана, основное уравнение теплопередачи.

Непосредственный жизненный опыт и точные физические измерения показывают, что количество передаваемого в пространстве тепла прямо пропорционально продолжительности процесса, поверхности теплообмена и, как правило, температурному напору: Q* = AΔ τ F Δ t, (1) где А – коэффициент пропорциональности, зависящий от вида и характера процесса, размеров и свойств тел, многих режимных факторов. В случае теплоотдачи коэффициент пропорциональности называют коэффициентом теплоотдачи а, а формулу (2. 1) после деления на Δ τ и F записывают в виде закона Ньютона-Рихмана: q = α Δ t, где Δ t = tс − tж (или Δ t = tж − tс, если температура теплоносителя больше, чем температура стенки tc), а величина α представляет собой количество тепла, которое передается теплоотдачей через единицу поверхности за единицу времени при разности температур между стенкой и теплоносителем в один градус. Величина α зависит от многих факторов, о чем будет рассказано позже, и часто определяется по результатам экспериментальных исследований процессов теплоотдачи. При теплопередаче формула (1) записывается в виде основного уравнения теплопередачи: q = k (tж1 − tж2 ), где коэффициент пропорциональности k называют коэффициентом теплопередачи, a tж1 и tж2 – температуры горячего и холодного теплоносителей вдалеке от стенки, соответственно. Для многих простых задач величину k нетрудно рассчитать, если известны величины α 1 и α 2, толщина и теплопроводность стенки. Для процессов теплопроводности указать однозначно величину Δ t, как это было в предыдущих случаях, невозможно. Поэтому в формулу (1) введем сначала относительный температурный напор Δ t / Δ n и величину AΔ n будем рассматривать как некий коэффициент пропорциональности, который называют коэффициентом теплопроводности λ. Этот коэффициент показывает, сколько тепла будет передано теплопроводностью через единицу поверхности за единицу времени при разнице температур в один градус, приходящейся на каждый метр пути теплового потока. Величина λ зависит только от свойств вещества и является его физконстантой, характеризующей способность тела проводить тепло. Если перейти к бесконечно малым приращениям и величину Δ t / Δ n заменить соответствующей производной, то после деления на Δ τ и F из приведенной формулы получаем известное выражение закона Фурье для теплопроводности: Знак минус отражает здесь разную направленность векторов q и grad t. В дальнейшем направления этих векторов будем считать определенными и не отмечать в приводимых формулах. Исключение из закономерности (2. 1) составляет тепловое излучение, где в соответствии с законом Стефана-Больцмана количество излучаемой энергии пропорционально не температурному напору, а абсолютной температуре излучающей поверхности в четвертой степени (в идеальном случае, для абсолютно черного тела): Q = σ Δ τ F T 4 s или q = σ s T 4; здесь σ S – постоянная Стефана-Больцмана – одна из универсальных физических констант.

76. Дифференциальное уравнение теплопроводности (вывод), его физический смысл. Запишем выражение первого закона термодинамики для процесса теплопроводности, протекающего в течение элементарно малого промежутка времени dτ: dU = dQ* − dLЗдесьdU – изменение внутренней энергии в выделенном объеме; dQ* – количество тепла, вносимого в объем теплопроводностью; dL – работа, совершаемая элементом против внешних сил. Отметим, что dL = pd (dV) = 0, (dV = dxdydz), поскольку дифференциал бесконечно малой величины есть величина бесконечно малая величина второго порядка малости и ею можно пренебрегать. Тогда предыдущая формула упрощается: dU = dQ* (1). Из термодинамики известно, чтоdU = c dmdτ t = cρ dV · ∂ t/∂ τ · ∂ τ, Величину dQ* представим тремя слагаемыми dQ* = dQ*x + dQ*y + dQ*z (2), и более подробно рассмотрим лишь составляющую по направлению х. Если через qx и qx + dx обозначим удельные тепловые потоки, направленные по оси х, первый из которых входит в элемент, а второй – выходит из него (см. рис. 2. 4), то количество тепла, накапливающееся в выделенном объеме по направлению х, будет: dQx* = qxdydzdτ − qx+dxdydzdτ = (qx − qx+dx )dydzdτ. Поскольку функция qx = f (x) непрерывна (для распространения тепла нет препятствий), то связь между предыдущим значением функции и ее последующим значением определяется известной формулой Тейлора. Всеми слагаемыми ряда, начиная с третьего, можно пренебрегать как величинами более высоких порядков малости. Тогда формулу можно переписать: . Аналогичные рассуждения, если рассмотреть направления у и z, позволяют получить аналогичные по структуре выражения для * ydQ и * dQz. Тогда формула (2) может быть представлена так: , Сумму частных производных проекций вектора, выделенную скобками, называют дивергенцией вектора и обозначают словом div. Поэтому предыдущее выражение часто записывают по другому: dQ* = –divq – dVdτ (3). Воспользуемся теперь законом Фурье, который в проекциях на координатные оси дает: , Подставляя эти выражения, получим: , Подставим теперь в формулу (1) значения dU и dQ*, соответственно. После сокращения получаем: , Если преобразовать формулу (3), то дифференциальное уравнение теплопроводности можно получить в виде: , Это более общая запись, в ней не предполагается, что λ = const. Сумму вторых частных производных скалярной величины по направлениям координатных осей называют оператором Лапласа и обозначают для краткости символами ∇ 2. Множительλ /(сρ ), составлен из физконстант и представляет собою некоторую обобщенную физконстанту, характеризующую способность тел проводить тепло и одновременно аккумулировать его (при нагреве). Эту характеристику называют коэффициентом температуропроводности а: a = λ / (сρ ), поскольку его величина определяет и скорость изменения температуры в любой фиксированной точке тела. Коэффициент а имеет важное значение только для нестационарных процессов. В итоге дифференциальное уравнение теплопроводности записывается очень компактно: ∂ t / ∂ τ = a∇ 2t. Этоуравнениеописывает связь между изменением температуры в пространстве (правая часть) и по времени (левая часть) в окрестностях любой точки внутри тела и представляет основу для решения всего класса задач теплопроводности. Часто это уравнение называют дифференциальным уравнением Фурье

77. Условия однозначности в задачах теплопроводности (геометрические, физические, начальные и граничные). Для решения практических задач энергосбережения в строительстве и промышленности требуется знание теплового потока, градиента температур, распределения температур внутри объема тела. Поэтому для каждого конкретного случая к дифференциальному уравнению теплопроводности добавляют математические условия или ряд дополнительных уравнений, называемых условиями однозначности задачи. Условия однозначности включают в себя геометрические, физические, временные и граничные условия. Геометрические условия характеризуют геометрические и линейные размеры тела, участвующего в процессе теплообмена. Физические условия характеризуют физические свойства тела, среды (λ, с, ρ, а) или задается закон внутреннего тепловыделения. Временные или начальные условия характеризуют особенности протекания процесса во времени или распределение температуры внутри тела в начальный момент времени: при τ =0 и Т=f(x, y, z). Очень часто в начальный момент времени тело имеет равномерную одинаковую температуру по всему объему: τ =0 и Т=Т0=const. Граничные условия характеризуют процессы теплообмена между поверхностью тела и окружающей средой. Граничные условия задаются несколькими возможными случаями: Ι рода – задается распределение температуры на поверхности тела: Тп=f (x, y, z, τ ); очень часто Тп=const. Ι Ι рода – задается распределение теплового потока на поверхности тела: qп=f (x, y, z, τ ); очень часто qп=const. Ι Ι Ι рода – задаются температура окружающей среды Тс и закон теплообмена между средой и поверхностью тела. Эти законы зависят от многих факторов и поэтому, чаще всего, используется закон теплообмена Ньютона: q=α (Тп − Тс) или − λ (dТ/dn)=α (Тп − Тс). Ι V рода (условия сопряжения) – характеризуют процессы теплопроводности между соприкасающимися поверхностями различных тел, когда температура в точке сопряжения тел одинакова, но тепловые потоки разные.

78. Методы решения краевой задачи в теории теплопроводностиВсе методы решения краевой задачи теории теплопроводности можно разделить на две большие группы. К первой группе относят методы, использующие современные средства математического анализа, вычислительной математики и вычислительной техники, поэтому их называют теоретическими методами. Во вторую группу включены методы, при использовании которых, температурное поле находят в результате проведения эксперимента. Поэтому их называют экспериментальными методами. Экспериментальные методы делятся на методы теории подобия и методы аналогий. По методу теории подобия температурное поле находят экспериментально на модели, в которой реализуется процесс той же физической природы, что и в объекте моделирования. По методу аналогий исследование процесса теплопроводности заменяется исследованием процесса другой физической природы, который протекает аналогично процессу теплопроводности. Эта аналогия проявляется в одинаковых по форме записи дифференциальных уравнениях переноса, относящихся к разным физическим явлениям. Теоретические методы можно подразделить на аналитические, численные, численно-аналитические методы. При использовании аналитических методов решение получают в виде конечной формулы или бесконечного ряда. Различают точные аналитические методы (метод разделения переменных или метод Фурье, метод интегральных преобразований, метод конформных отображений и др. ) и приближенные аналитические методы (различные формы вариационных методов, метод подстановок и др. ). Точные аналитические методы можно применять только к линейным задачам теории теплопроводности. При использовании численных методов решение задачи получают в виде набора значений температур в дискретных точках пространства в дискретные моменты времени. В настоящее время для методами решения задач теплообмена наиболее часто используют метод сеток и метод конечных элементов. Методы, которые используют аналитические решения для получения значений температур в дискретных точках пространства в дискретные моменты времени, называются численно-аналитическими (метод граничных элементов, метод R-функций, метод дискретного удовлетворения краевых условий и др. ). В результате решения задачи нестационарной теплопроводности находят температурное поле, изменяющееся в пространстве и во времени. Точные аналитические решения дифференциального уравнения теплопроводности для тел простейшей формы с граничными условиями I, II и III родов приведены в методических указаниях " Нестационарная теплопроводность" №1684. Для удобства инженерных расчетов аналитическое решение при ГУ III рода представлено в виде графиков – номограмм, которые для тел простейшей формы также приведены в той же методичке №1684. Поэтому далее рассмотрим постановку задачи и алгоритм определения температурного поля с помощью номограмм.

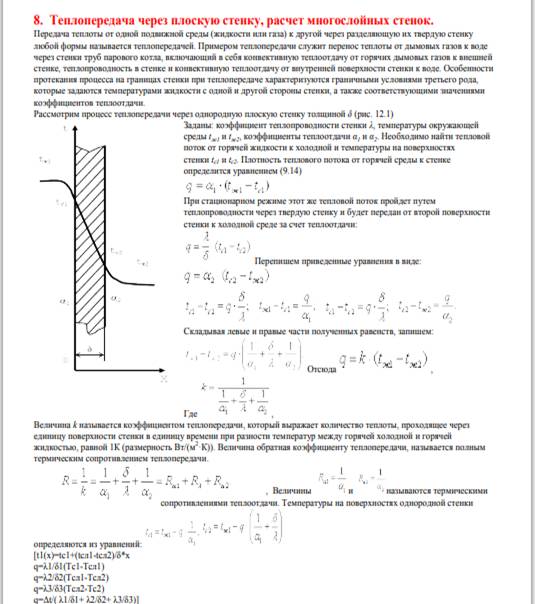
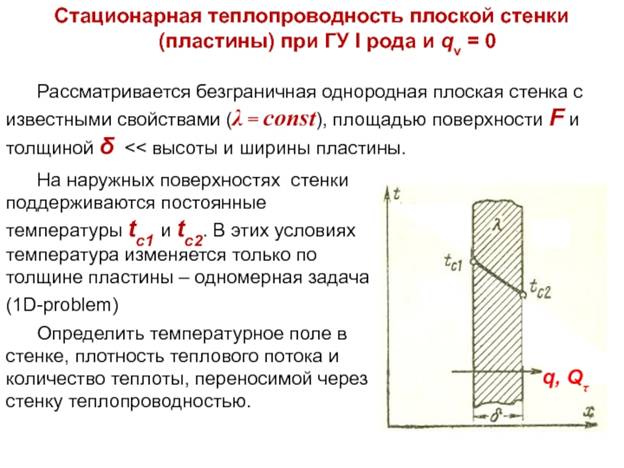
79. Стационарная теплопроводность плоской стенки при граничных условиях первого и второго рода (вывод).

80. Теплопередача через плоскую стенку, расчет многослойных стенок (вывод).

81. Стационарная теплопроводность цилиндрической стенки при граничных условиях первого и второго рода (вывод).

82. Теплопередача через цилиндрическую стенку, расчет многослойных цилиндрических стенок (вывод).

83. Критический диаметр изоляции (вывод). Условие эффективной изоляции труб. Оптимальная изоляция.

84. Стационарная теплопроводность через шаровую стенку (вывод).

85. Теплопередача через ребристую стенку (вывод). Коэффициент эффективности оребрения.

86. Одномерное температурное поле в плоском ребре (вывод). Коэффициент эффективности ребра.

87. Температурное поле в круглом ребре прямоугольного профиля (вывод). Коэффициент эффективности ребра.

Эффективность ребра определяется как отношение теплового потока, действительно передаваемого ребром, к тепловому потоку, который передавало бы такое же идеально проводящее ребро (Я = со) с однородной температурой, равной температуре в основании ребра. Для продольного ребра прямоугольного профиля эффективность определяется по формуле ІІптН.

88, Стационарное температурное поле в плоской стенке при наличии тепловыделений и симметричных условия отвода теплоты от пластины (вывод).

89. Стационарное температурное поле в плоской стенке при наличии тепловыделений и разными температурами поверхностей (вывод). Критерий Померанцева.

Теплопроводность через плоскую и цилиндрическую...

DomChtoNado. ru ›teploprovodnost-cherez-stenku. html

Распределение температуры в плоской стенке. Теплопроводность через многослойную стенку. Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода). ... Рассмотрим стационарный режим теплопередачи через плоскую, цилиндрическую и сферическую стенки при котором теплопередача - величина постоянная и температурное поле не изменяется во времени и зависит только от координаты. В этом случае при условии постоянства теплофизических свойств тела температура в плоской стенке изменяется линейно, а в цилиндрической - по логарифмическому закону, т. е. Q = const и T = f(x) - линейная (при плоской стенке ) или логарифмическая функция (при круглой стенке ).

критерий Померанцева. При отсутствии внутренних источНиковтеплоты q. = о уравнение превращается в уравнение для охлаждаемой оДнородной пластины

90. Стационарное температурное поле в однородном цилиндрическом стержня при наличии тепловыделений (вывод).

Стационарное температурное поле

На рис. 7. 1 изображен стержень круглого сечения и радиуса а. Длина стержня в направлении оси oz неограниченно велика. В стержне имеются внутренние источники тепла, их объемная плотность равна q_v. Известны также теплопроводность к, плотность р и теплоемкость стержня С_р. Теплопроводность и теплоемкость зависят от температуры, а объемная плотность внутренних источников тепла является функцией координаты г. На поверхности стержня известны условия теплообмена — это граничные условия первого, второго или третьего рода. Требуется получить аналитические выражения для температуры и плотности теплового потока и на их основе сформировать каскадную схему замещения для расчета температурного поля в стержне.

Температурное поле в стержне описывается следующим стационарным уравнением теплопроводности:

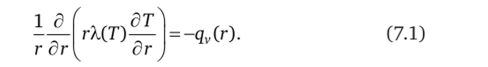
Разобьем расчетную область на элементарные кольца (рис. 7. 2). В каждом кольце теплопроводность к, теплоемкость С_р и плотность внутренних источников тепла q_v имеют постоянное значение. На границах кольца известны температуры Г_а и Т₂, и плотности теплового потока q_/A и q_{/ 2}-

91. Нестационарное температурное поле в процессе охлаждения (нагревания) пластины (вывод).

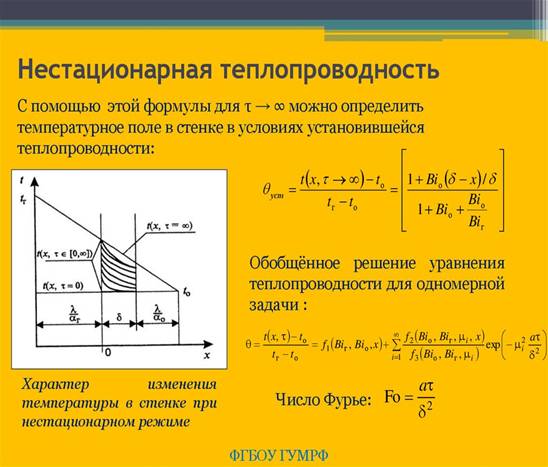
92. Нестационарное температурное поле в процессе охлаждения (нагревания) бесконечно длинного цилиндра (вывод).

93. Охлаждение (нагревание) тел, имеющих форму параллелепипеда или цилиндра конечных размеров (вывод). Метод перемножения решений.

94. Регулярный тепловой режим. Темп охлаждения.

95. Основные положения конвективного теплообмена в однофазной среде.

Конвекция теплоты осуществляется за счет перемещения макрообъемов среды из области с одной температурой в область с другой температурой. Конвекция протекает совместно с процессом теплопроводности. Сочетание конвекции и теплопроводности, наблюдаемое в текучих средах, называют конвективным теплообменом. Поэтому плотность теплового потока при конвективном теплообмене рассчитывается по формуле:

qкто=qконд+qконв=-l× Ñ T +r× w × h,

где qкто – плотность теплового потока при конвективном теплообмене, Вт/м2; qконд – плотность теплового потока при кондуктивном (за счет теплопроводности) теплообмене, Вт/м2; qконв – плотность теплового потока за счет конвекции текучей среды, Вт/м2; l – коэффициент теплопроводности флюида, Вт/(м2 ·К); Ñ T – градиент температур, К/м; r – плотность флюида, кг/м3; w – скорость движения флюида, м/с; h =cp× T – удельная энтальпия флюида, Дж/кг; T – температура, º C или К.

Таким образом, для расчета теплового потока, передаваемого в неизотермической текучей среде необходимо предварительно рассчитать температурное поле и поле скорости.

В зависимости от причины, вызывающей движение текучей среды, различают конвекцию при вынужденном движении или вынужденную конвекцию и конвекцию при свободном движении или свободную конвекцию. При вынужденной конвекции движение текучей среды происходит под действием внешней силы – разности давлений в потоке, которую создает какое-либо транспортирующее флюид устройство, например, вентилятор, насос и т. п. При свободной конвекции движение среды происходит без приложения внешней силы, а вследствие разности плотностей различных объемов среды, которая может возникать из-за переменного поля температуры, т. к. плотность r= f(T). Переменное поле температур вызывает переменное поле плотности и, вследствие этого, в поле земного тяготения происходит перемещение масс с разной плотностью ( легкие слои поднимаются вверх, тяжелые опускаются вниз). В этом случае говорят о свободной тепловой или естественной конвекции. Заметим, что переменная по объему плотность текучей среды может быть создана и путем механического перемешивания сред с различной плотностью (например, при продувке жидкой стальной ванны кислородом).

По интенсивности движения различают два основных режима течения: ламинарный и турбулентный. Для большинства флюидов существует и переходный от ламинарного к турбулентному режим течения.

Признаки ламинарного режима течения:

— частицы среды движутся по плавным взаимно непересекающимся траекториям;

— параметры течения (температура, скорость, давление и концентрация примесей) являются гладкими функциями координат и времени;

—перенос субстанции (теплоты, импульса и массы) осуществляется за счет взаимодействия микрочастиц среды (атомов, молекул, ионов и т. п. ). Поэтому коэффициенты переноса субстанции (коэффициент температуропроводности, коэффициент кинематической вязкости и коэффициент диффузии) являются физическими характеристиками вещества. Коэффициенты переноса субстанции для разных веществ определяют экспериментально и приводят в справочных таблицах в зависимости от температуры.

Признаки турбулентного режима течения:

— частицы среды движутся по сложным, ломаным, взаимно пересекающимся траекториям; Бухмиров В. В. Лекции по ТМО декабрь, 2008_часть2_в7 2

— параметры течения (температура, скорость, давление и концентрация примесей) являются пульсирующими функциями координат и времени;

—перенос субстанции (теплоты, импульса и массы) осуществляется за счет взаимодействия макрообъемов среды (турбулентных молей). Поэтому коэффициенты переноса субстанции (коэффициент температуропроводности, коэффициент кинематической вязкости и коэффициент диффузии) зависят от самого режима движения и не являются физическими характеристиками вещества. Коэффициенты турбулентного переноса субстанции рассчитывают по, так называемым, полуэмпирическим моделям турбулентности, изучение которых выходит за рамки нашего краткого курса.

Существование ламинарного или турбулентного режима течения зависит от соотношения двух сил, действующих в текучей среде: силы инерции (f ин)и силы трения (f тр). При условии ин f тр< < f имеет место ламинарный режим течения и, соответственно, наоборот, при ин тр f > > f – турбулентный режим.

96. Дифференциальные уравнения конвективного теплообмена.

97. Понятие о гидродинамическом и тепловом пограничных слоях.

98. Основы теории подобия. Получение критерия Нуссельта и его физический смысл.

Современная наука предлагает исследователю три основных подхода для решения инженерных задач. Всегда предпочтительно аналитическое решение, поскольку оно дает общий результат, удобный для расчетов и наглядно отражающий влияние одних факторов на другие. Однако любая математическая модель, любые дифференциальные уравнения всегда лишь в главном, в основном отражают свойства и особенности реального явления. Именно поэтому достоверность и точность аналитического решения нуждаются в подтверждении экспериментами. К сожалению, как было сказано выше, многие практические задачи аналитически неразрешимы. Правильно поставленный эксперимент гарантирует достоверность результата. Однако это результат единичный, не способный дать пищу для обобщений или прогнозирования изменений при изменении условий опыта. Поэтому всегда речь ведется о проведении серии или многих серий опытов, что долго, трудоемко и дорого. Численное решение задач на ЭВМ как бы объединяет оба предыдущих подхода, поскольку здесь оперируют с математической моделью явления и получают единственное решение задачи, не обладающее, увы, ни общностью, ни достоверностью результата. Однако при наличии программы не представляет трудностей провести множество численных экспериментов (так еще по другому называют этот подход) и выявить важнейшие закономерности явления. Поэтому сегодня такой подход получил самое широкое распространение, сделавшись самым мощным инструментом ученого и инженера. При экспериментальных исследованиях обычно ставится задача установить количественную зависимость одного или ряда определяемых параметров от величины других определяющих факторов. Чтобы сделать это, опыты проводят отдельными сериями так, чтобы в каждой серии изменялся только один влияющий фактор, остальные же оставались бы неизменными. При оптимальном планировании экспериментов от этого правила отступают, уменьшая число требуемых серий. Однако всегда экспериментальное исследование связывается с большим числом отдельных экспериментов. Теория подобия позволяет существенно сократить число необходимых опытов и обобщать их результаты в понятной и удобной для практики форме. Сущность подхода здесь простая: все явления одного класса (теплопроводность, конвекция и др. ) делят на отдельные группы подобных явлений, выявив особые признаки такого подобия. Далее из множества явлений каждой группы экспериментально исследуют лишь малое число их, выявляя зависимости не между конкретными размерными величинами, а между обобщенными, безразмерными числами подобия, количество которых всегда меньше, чем размерных параметров. Результаты опытов обобщают в виде полуэмпирических формул, которые однако справедливы для всех явлений данной группы. Два явления считают подобными, если для всех одноименных параметров в любых сходственных точках и в сходственные моменты временимеютместо соотношения:

99. Система критериев конвективного теплообмена (критерии Nu, Re, Pr, Gr), критериальные уравнения и способы организации экспериментов и обработки опытных данных.

100. Методы экспериментального определения коэффициентов теплоотдачи. Осреднение коэффициентов теплоотдачи

101. Осреднение температуры жидкости по сечению. Осреднение температуры жидкости и температурного напора по длине трубы

Если температура изменяется незначительно, то осреднение температуры по длине производится следующим образом. При небольшом изменении средней температуры вдоль трубы величина может быть определена как среднее арифметическое из значений средних температур в начальном и конечном сечениях трубы: . Изменение температурного напора вдоль трубы при. а — охлаждение жидкости; б — нагрев жидкости. . Распределение скоростей по сечению при неизотермическом ламинарном течении жидкости в трубе. ... При значительном изменении температуры по сечению и длине трубы в разных точках потока оказываются различными плотности жидкости или газа.

102. Получение эмпирических критериальных уравнений. Определяющий размер. Определяющая температура

Теория подобия может дать только общий вид критериального уравнения, т. е. определяет форму, в которой следует проводить обобщение экспериментальных данных. Например, для теплоотдачи в трубе при развитом турбулентном режиме теория подобия дает Nu =/(Re, Рг). Обычно подобные функциональные зависимости аппроксимируются степенными функциями, т. е. полагают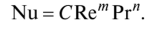

Определение входящих в формулу постоянных коэффициентов С, тип — задача экспериментального исследования.

В качестве примера рассмотрим способ получения критериального уравнения для теплоотдачи при развитом турбулентном течении в трубе

(Re »Re_Kp = 2300).

Пусть для какого-либо конкретного режима 1 определен расход жидкости (7, = vvjpF, F =. Будем полагать, что жидкость несжимаема (р = const).

Для этого режима найдем число Рейнольдса Rej = v = f(T),

по средней скорости потока w,

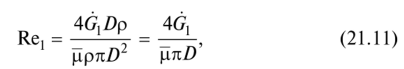
Чтобы определить число Нусселъта Nuj = X = f(T), необ-

ходимо экспериментально найти средний коэффициент теплоотдачи. Для этого воспользуемся уравнением Q_{ =a_xnDL(T_w - Т), где Q - VI — тепловой поток от электронагревателя к потоку. Тогда

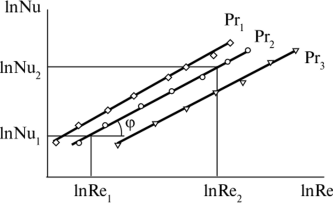
Изменяя расход и тепловую нагрузку, построим график в координатах InNu-InRe (рис. 21. 7). Обработка точек методом наименьших квадратов дает экспериментальную прямую. Тангенс угла наклона

103. Общие сведения о свободной конвекции. Число Релея.

Число Рэлея — безразмерное число, определяющее поведение жидкости под воздействием градиента температуры. Если число Рэлея больше некоторого критического значения, равновесие жидкости становится неустойчивым и возникают конвективные потоки: Ra=GrPr=gβ Vlo 3 /υ a, α

будет зависеть от свойств жидкости, температурного напора, формы и размера тела, его

расположения.

104. Теплоотдача при свободной конвекции жидкости около вертикальной пластины или вертикальной трубы.

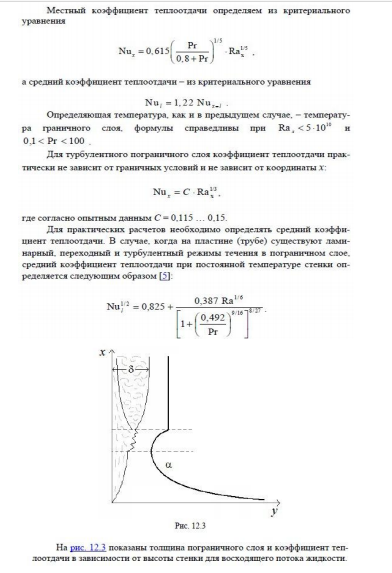
105. Теплоотдача при свободной конвекции жидкости около горизонтальной пластины и горизонтальной трубы.

106. Свободная конвекция в ограниченном пространстве. Эквивалентный коэффициент теплопроводности.

107. Теплоотдача при продольном обтекании пластины.

108. Теплоотдача при поперечном обтекании одиночного цилиндра.

109. Теплоотдача при поперечном обтекании пучков труб.

110. Гидродинамика и теплообмен при течении жидкости в трубах и каналах. Участки гидродинамической и тепловой стабилизации

111. Влияние силы тяжести на теплообмен при течении жидкости в трубах. Вязкостный и вязкостно-гравитационный режимы теплоотдачи

При ламинарном течении жидкости встречаются два режима неизотермического движения: вязкостный и вязкостно-гравитационный.

Вязкостный режим соответствует течению вязких жидкостей при отсутствии естественной конвекции. В этом режиме передача теплоты к стенкам канала (и наоборот) осуществляется только теплопроводностью.

Вязкостно-гравитационный режим имеет место, когда вынужденное течение жидкости сопровождается естественной конвекцией. В этом режиме теплота передаётся не только теплопроводностью, но и конвекцией.

Распределение скоростей зависит от направления теплового потока:

при нагревании жидкости её температура у стенки выше температуры основного потока, а вязкость меньше и скорость выше («правильный» D-профиль); при охлаждении процессы протекают в обратном направлении («вытянутый» D-профиль).

Следовательно, при нагревании жидкости её скорость у стенки больше, чем при охлаждении, и теплоотдача выше.

При вязкостно-гравитационном режиме важно отметить направление свободной конвекции и вынужденного движения. Они могут совпадать, быть противоположны друг другу, быть взаимно перпендикулярными.

При совпадении движений естественной и вынужденной конвекции скорость жидкости у стенки возрастает и теплоотдача увеличивается (вертикальные трубы).

При противоположном направлении движений вынужденной и естественной конвекции скорость у стенки уменьшается и теплоотдача падает, но когда у стенки образуется вихревое движение, теплоотдача увеличивается (движение нагреваемой жидкости сверху вниз).

При взаимно перпендикулярном движении естественной и вынужденной конвекции вследствие лучшего перемешивания жидкости теплоотдача увеличивается (горизонтальные трубы, где жидкость движется как бы по спирали).

Т. о., в неизотермических условиях строго ламинарный режим не существует.

При вязкостном режиме средний коэффициент теплоотдачи в прямых гладких трубах

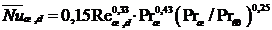
Для вязкостно-гравитационного режима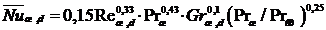

за определяющую скорость принята средняя скорость жидкости в трубе;

за определяющий размер – диаметр круглой трубы или эквивалентный диаметр.

Чтобы определить наличие влияния естественной конвекции, рассчитывают величину 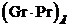, где определяющей температурой является .

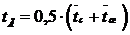Если 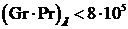, то режим вязкостный, и вязкостно-гравитационный, если наоборот.

Для труб, с l/d< 50 следует значение α умножить на средний поправочный коэффициент 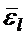~1, 0-2, 0

112. Теплоотдача при ламинарном и турбулентном течении жидкости в гладких трубах.

113. Теплоотдача в изогнутых и некруглых трубах.

114. Основные положения теплообмена при конденсации чистых паров.

Процесс перехода вещества из парообразного состояния в жидкое называется конденсацией. Конденсация пара может происходить как в его объеме, так и на охлаждаемой поверхности. При конденсации на поверхности обязательно должно быть переохлаждение поверхности ниже температуры насыщения при данном давлении пара. Конденсация в объеме не происходит даже при значительном переохлаждении пара. Поэтому непременным условием объемной конденсации является наличие центров конденсации. Их роль могут выполнять пылинки или ионизированные частицы. В промышленных аппаратах конденсация происходит главным образом на поверхности теплообмена. При этом различают два вида конденсации: пленочную и капельную. При пленочной конденсации вся охлаждаемая поверхность покрывается сплошной пленкой конденсата. Такой вид конденсации происходит на поверхностях, которые хорошо смачиваются данной жидкостью. Пленка конденсата создает значительное термическое сопротивление, снижая интенсивность теплообмена. Толщина конденсатной пленки зависит от следующих факторов: · положения поверхности; · состояния поверхности; · свойств жидкости; · направления и скорости движения пара. Капельная конденсация происходит на поверхностях, которые не смачиваются данной жидкостью. На такой поверхности конденсат накапливается в виде отдельных капель, которые по мере пополнения их жидкостью скатываются с нее. Теплоотдача при капельной конденсации примерно в 10 раз больше, чем при пленочной, т. к. большая часть охлаждаемой поверхности находится в непосредственном контакте с паром. Аналитическое решение задачи о теплоотдаче при пленочной конденсации было выполнено Нуссельтом. Коэффициент теплоотдачи определяется по формуле: 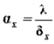, где λ - коэффициент теплопроводности конденсата; δ _x – толщина пленки конденсата. При конденсации пара на вертикальных поверхностях конденсатная пленка стекает и толщина ее изменяется по высоте. В таких случаях теплообмен со стенкой высотой H может быть описан средним значением коэффициента теплоотдачи: 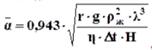, где r – теплота парообразования при температуре насыщения; ρ _ж – плотность конденсата; η - вязкость конденсата; Δ t = (tн – tст); tн – температура насыщения пара; tст – температура стенки. Для движущегося пара значения коэффициента теплоотдачи могут быть больше или меньше по сравнению с неподвижным паром. Коэффициент теплоотдачи увеличивается с повышением скорости движения пара, если его поток уменьшает толщину конденсатной пленки или срывает ее с поверхности. Если же поток пара препятствует движению пленки и при этом не срывает ее с поверхности, то увеличение скорости пара приводит к уменьшению коэффициента теплоотдачи. При шероховатых поверхностях коэффициенты теплоотдачи меньше, чем при гладких, т. к. их сопротивление течению пленки больше и, следовательно, меньше скорость стекания пленки и больше ее толщина.

115. Термические сопротивления в процессе конденсации пара на охлаждаемой стенке

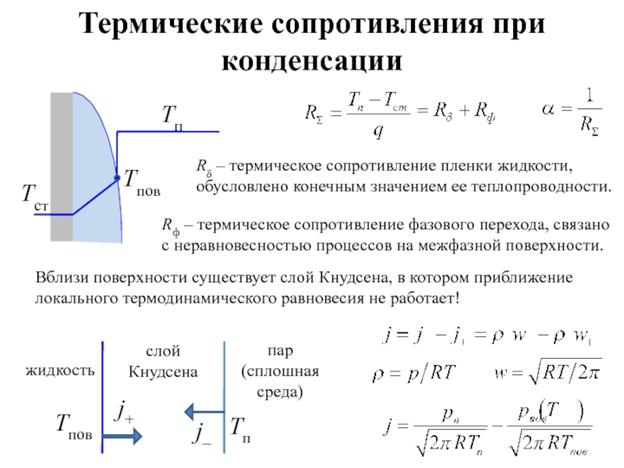
116. Теория пленочной конденсации на охлаждаемой вертикальной стенке.

35. Теплоотдача при пленочной конденсации неподвижного пара. Пленочная конденсация имеет место при соприкосновении водяного пара с чистой металлической поверхностью. Капли, выпадающие на поверхности, растекаются и образуют сплошную пленку. Необходимо знать, что любая чистая поверхность металла постепенно покрывается загрязнениями и плохо смачивается, но с течением времени (в процессе старения поверхности) образуется оксидная пленка, на которой конденсация, рано или поздно, приобретает пленочный характер. Поэтому капельная конденсация особого интереса для инженеров не представляет, хотя при капельной конденсации теплообмен между паром и стенкой в 5 - 10 раз больше, чем при пленочной конденсации