студент-отличник - студент-неотличник

Сравнимые и несравнимые понятия. Отношения между понятиями

Если мы будем сравнивать различные понятия по их содержанию, то обнаружим, что содержания одних понятий включают общие признаки, а содержания других понятий таких признаков не имеют.

Так, в содержании понятий «рассказ» и «поэма» есть общий признак «быть художественным произведением»». Но сравним понятия «трапеция» и «ля-бемоль». Содержание первого понятия - «быть четырехугольником» и «иметь две параллельные стороны». Содержание второго - «быть нотой» и «звучать на полтона ниже ноты ля». Нет общих признаков.

Первые два понятия мы назовем сравнимыми, а вторые несравнимыми. Дадим определения.

Понятия называются сравнимыми, если в их содержаниях имеются общие признаки или свойства, и называются несравнимыми, если в их содержаниях нет общих признаков или свойств.

Можно определить и иначе: понятия сравнимы, если они имеют общее для них родовое понятие, и несравнимы, если не имеют общего родового понятия.

Поэтому сравнимыми будут понятия «окунь» и «карп», т. к. существует родовое понятие «рыба», которое включает в свой объем как окуней, так и карпов; сравнимы понятия «человек» и «еж» – имеют общее родовое понятие «млекопитающее». Сравнимыми будут такие разнопорядковые понятия, как «окунь», «человек», «боярышник», «роза», «растение», «осьминог», «куропатка» – их объемы войдут в объем родового понятия «живое существо».

Но понятия «планета» и «синус угла α », не являются сравнимыми, так как для них нельзя подобрать соответствующего общего родового понятия.

Приведем еще примеры попарно несравнимых понятий: «слон» и «небоскреб», «щука» и «нож», «книжная полка» и «головоногие», «стул» и «нота ля», «диагональ» и «астероид Церера», «число, оканчивающееся на 5» и «понедельник».

Задание 5. Найдите в следующем списке сравнимые и несравнимые понятия.

Дерево, улитка, отбивная, автомобиль, каратэ, пальма, восточная борьба, ромб, повесть, шашлык, квадрат, рассказ, лыжи.

Итак, сопоставляя различные понятия по содержанию, мы можем говорить о них как сравнимых либо несравнимых.

Перейдем к отношениям между понятиями. Понятно, что между несравнимыми понятиями не может быть каких-либо отношений, а вот между сравнимыми понятиями могут быть те или иные отношения. Поэтому далее будем рассматривать только сравнимые понятия.

В то время как сравнение понятий мы проводим по их содержанию, отношение между понятиями определяется через сопоставление их объемов. В зависимости от того, совпадают объемы двух сравнимых понятий или не совпадают, они называются совместимыми или несовместимыми. Определения:

Понятия называются совместимыми, если их объемы полностью или частично совпадают, и несовместимыми, если их объемы полностью не совпадают.

Совместимыми будут понятия «лошадь» и «млекопитающее». Дело в том, что весь объем первого понятия является частью объема второго понятия, так как все лошади являются млекопитающими.

Несовместимыми будут понятия «окунь» и «карп», потому что ни один элемент объема первого понятия не входит в объем второго понятия и наоборот. Или по-другому - ни один окунь не является карпом, и не один карп не является окунем.

Рассмотрим типы отношений сначала между совместимыми понятиями.

1. Отношение подчинения или субординации. При этом отношении некоторые элементы объема одного понятия входят в объем второго понятия, и все элементы объема второго понятия входят в объем первого понятия. Первое понятие называется подчиняющим, второе – подчиненным.

Круговая схема и суждения отношения подчинения: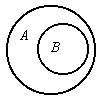

Некоторые А есть В. Все В есть А.

Здесь А - подчиняющее понятие, В - подчиненное понятие. Присматриваясь к этим понятиям, мы обнаруживаем, что первое из них является родовым по отношению ко второму, а второе является видовым по отношению к первому. Примеры:

Подчиняющие понятия планета элементарная частица человек летательный аппарат

Подчиненные понятия планета Солнечной системы электрон Николай Петров дирижабль

Выразим отношение этих пар понятий через пары суждений:

Некоторые планеты являются планетами Солнечной системы.

Все планеты Солнечной системы являются планетами.

Некоторые элементарные частицы являются электронами.

Все электроны являются элементарными частицами.

И т. д.

2. Отношение равнозначности, или эквивалентности. При этом отношении все элементы объема одного понятия входят в объем второго понятия, и наоборот, все элементы объема второго понятия входят в объем первого понятия.

Таким образом, речь идет о понятиях, объемы которых полностью совпадают, хотя их содержания различны.

Круговая схема и суждения отношения равнозначности: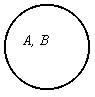

Все А есть В. Все В есть А.

Рассмотрим понятия «дочь» и «внучка». Эти понятия имеют разное содержание, но объемы их совпадают. Действительно, можно сформулировать следующие суждения:

Все дочери являются внучками.

Все внучки являются дочерьми.

Поэтому эти понятия равнозначны. Другие примеры:

планета Земля - обитаемая планета Солнечной системы

ромб с равными углами - прямоугольник с равными сторонами

граф Лев Толстой - автор романа «Война и мир»

число 5 - целое число, которое больше 4 и меньше 6

3. Отношение пересечения. При этом отношении некоторые элементы объема одного понятия входят в объем второго понятия, и некоторые элементы объема второго понятия входят в объем первого понятия.

Круговая схема и суждения отношения пересечения: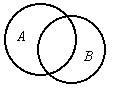

Некоторые А есть В. Некоторые В есть А.

Примеры понятий, находящихся в отношении пересечения:

глава государства - женщина

студент - шахматист-любитель

человек, говорящий по-английски, - инженер

Выразим отношение одной из пар понятий через суждения:

Некоторые главы государства являются женщинами.

Некоторые женщины являются главами государства.

Задание 6. Определите, какие понятия находятся в отношении подчинения, равнозначности и пересечения.

Сын; планета Марс; индеец; солнечный день; разумное существо; коренной житель американского континента; число, которое делится без остатка на 4; юноша; понедельник; внук; планета Солнечной системы с двумя естественными спутниками; число, которое оканчивается на 2; день рождения революционера Че Гевары

Перейдем к отношениям между несовместимыми понятиями. Напоминаем, что у несовместимых понятий объемы полностью не совпадают.

4. Отношение соподчинения, или координации. При этом отношении ни один элемент объема одного понятия не входит в объем другого понятия, и оба понятия подчинены общему родовому понятию.

Круговая схема и суждения отношения соподчинения: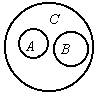

Ни одно А не есть В. Ни одно В не есть А.

Примеры понятий, находящихся в отношении соподчинения:

треугольник - прямоугольник (общий род - геом. фигура)

соната Бетховена - сонет Шекспира (общ. род - произв. искусства)

яхта - автомобиль (общий род - транспорт)

Суждения, выражающие отношение одной из пар понятий:

Ни один треугольник не является прямоугольником.

Ни один прямоугольник не является треугольником.

5. Отношение противоположности, или контрарности. При этом отношении одно понятие содержит признаки, несовместимые с признаками другого понятия, и суммарный объем обоих понятий не исчерпывает объем общего родового понятия.

Круговая схема и суждения отношения противоположности: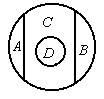

Ни одно А не есть В. Ни одно В не есть А.

На круговой схеме видно, что между объемами понятий А и B располагается объем промежуточного понятия D.

Примеры понятий, которые находятся в отношении противоположности:

сильный - слабый (существует промежут. состояние средней силы)

студент-отличник - студент-двоечник (существуют студенты просто хорошей успеваемости)

Север - Юг (есть среднее положение - экватор)

Суждения, соответствующие одной из пар понятий:

Ни один студент-отличник не являются студентом-двоечником.

Ни один студент-двоечник не является студентом-отличником.

6. Отношение противоречия, или контрадикторности. При этом отношении одно понятие содержит признаки, отсутствующие у другого понятия, и суммарный объем обоих понятий совпадает с объемом общего родового понятия.

Круговая схема и суждения отношения противоречия: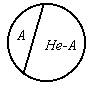

Ни одно А не есть не-А. Ни одно не-А не есть А.

Примеры понятий, находящихся в отношении противоречия:

студент-отличник - студент-неотличник

прекрасное - непрекрасное

сын - дочь

Суждения:

Ни один студент-отличник не есть студент-неотличник.

Ни один студент-неотличник не есть студент-отличник.