- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа №. Тема. Доказательство теоремы о трех перпендикулярах. Определение и построение угла между прямой и плоскостью, двугранного угла.. Методические рекомендации. Теоремы о трех перпендикулярах. Рассмотрим решение нескольких задач
Практическая работа №
Тема. Доказательство теоремы о трех перпендикулярах. Определение и построение угла между прямой и плоскостью, двугранного угла.
Цели: изучить теорему о трех перпендикулярах и показать ее применение при решении задач; познакомиться с определением и построением угла между прямой и плоскостью, двугранного угла
В результате выполнения практической работы обучающийся
должен знать: методы использования теоремы, методы построения углов.
должен уметь: решать задачи с использованием методов.
Форма проведения работы: практикум
Методические рекомендации
|
Теоремы о трех перпендикулярах | |
|
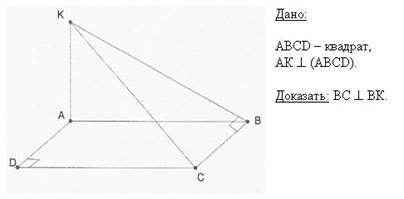
| Теорема (прямая). Прямая, проведенная на плоскости через основание наклонной перпендикулярно ее проекции, перпендикулярна и самой наклонной. |
| Теорема (обратная). Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. | |
Теорема о трех перпендикулярах — полезный инструмент для решения задач.
Рассмотрим решение нескольких задач
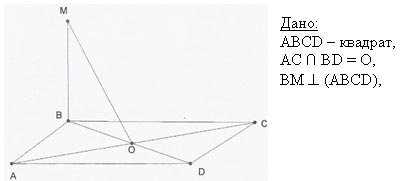
Задача 1. Из вершины А квадрата АВСD восстановлен перпендикуляр АК к его плоскости. Докажите, что ВС перпендикулярно КВ.
Доказательство:

Задача 2. Из вершины В квадрата АВСD восстановлен перпендикуляр ВМ к его плоскости. Докажите, что АС перпендикулярно МО (О – точка пересечения диагоналей).
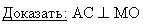

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|