Задание на СРСП для студентов 3 курса д.о. по дисциплина «Теория электрической связи»

Задание на СРСП для студентов 3 курса д. о. по дисциплина «Теория электрической связи»

ЗАДАНИЕ 1

Даны две последовательности прямоугольных импульсов амплитудой U_m = 2В, частотой f и скважностью g1 и g2, построить временные и спектральные диаграммы.

Исходные данные:

Номер варианта
Частота, КГц
Скважность g1
Скважность g2

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ

1. Временную диаграмму начертить в масштабе, определив период следования импульсов;

2. Для построения спектра необходимо рассчитать:

постоянную составляющую сигнала U₀ (это среднее значение сигнала за период ): U₀ = U_m t / T, где t – длительность импульса;
частота первой гармоники равна частоте следования импульсов;
частотный интервал между гармониками D f равен частоте первой гармоники;
амплитуды всех гармонических составляющих определяются выражением:

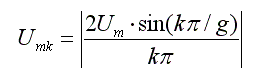
где k – номер гармоники;

g - скважность;

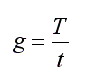ЗАДАНИЕ 2

Задано аналитическое выражение модулированного сигнала s(t). Назвать тип модуляции и построить спектральную диаграмму этого сигнала.

Номер варианта	s(t)









	< =" " >

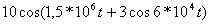
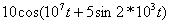
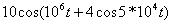
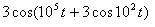
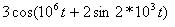
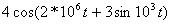
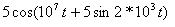
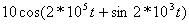
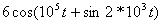МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ

1. Из математического уравнения следует, что это однотональная угловая модуляция с индексом m. При модуляции одним тоном модулирующий сигнал имеет вид:

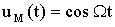
Аналитические выражения фазомодулированного (ФМ) и частотномодулированного (ЧМ)сигналов по форме записи имеют совершенно одинаковый вид:

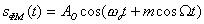
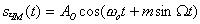
Отличие - только в порядке вычисления индекса и фазы модулирующего колебания. По заданному выражению сигнала определить амплитуду несущего колебания в вольтах, угловую частоту несущего колебания (рад/сек); угловую частоту модулирующего сигнала (рад/сек); индекс модуляции - m.

2. ФМ и ЧМ относятся к угловой модуляции. Если индексы модуляции одинаковы, то сигнал при угловой модуляции можно представить в виде:

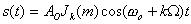где 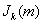- функция Бесселя k-ого порядка от аргумента m; спектр сигналов угловой модуляции сложнее спектра амплитудномодулированного сигнала, так как содержит бесконечное число верхних и нижних боковых частот. Боковые гармонические расположены симметрично относительно несущей частоты 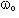на расстоянии 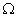. Амлитуды всех компонент спектра пропорциональны .

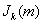Для детального анализа и построения спектральных диаграмм необходимо знание функций Бесселя при различных значениях k и m. Эти функции определяются из графика (см. математические справочники).

3. Cтроится спектральная диаграмма, по оси откладывается частота в Гц.

12 3 Следующая ⇒