lR. Дв:rраllныJj :'Гоп У!'О,'!меll\~1У ПJIOСКОСТЯМI1. -[\1НО]ОгртlllblС )I'Jlbl.

4. 1. К ПЛОСКОСIII а IIPOIH:. t~Ha IШКЛОIiIШЯ под УI" ЛОI\I зu ее проеКUlIЯ на ГJЛОСКОСiL а Р~IНШ 12 д. \I. Наiiти длl111У IIЭКЛОlltюl1, 11P0l3t1. LCHHOii к ПЛОСКОСТII а.

2, И'i точки отстояшей от плоскоеТl1 на раееJ'ШIНIII1 41\1 J! РОI! СЛС/Ш К П. lОе,: кости! I< 1КЛОIIIШЯ ДЛlIНОЙ 81\1, IlаЙПI угол между наклонной 11 плоскостью.

3, " о равнобе1. Lренном ПРЯ\IOУГОЛЫIOМ треУГОЛЬНlIке А" ОС катеты равны 2 См, Из I1СРШНIIЫ прямого угла С

проведен к ПJIOСКОСТИ ": }того треУГОЛЫШК< J перпеНДIlКУЛЯР СО, ПРIJчем СО-=:: 4 CJ\I. Н~ЙДlIТС раССТОЯllие от ТОЧК! \ О до ПНIOТСНУЗЫ ЛВ,

4, Высота праВНЛЬНОII 'lcTbIpeX) ГОJII, JlОЙ IlIlpa\НI, 'lI, 1 рarша 28 C\I, < J боковое ребро 36 C\I. НаЙДIIте сторону ОСНОRаНllЯ ПJlрам! \ды.

5, Под KaKII! \! ) глом К IIJiОСКОСПI lIадо провеСТII наклонную. чтобы ее проеКШНI была U. Jtюе \lСНLШС саМОII наклонноi1?

6, KOHU!. I ОТрt: 'и, а О" IСТ()ЯТ от ПЛОСКОСТII Р на раССТОЯНIIЯХ 1 СМ 11 4 СМ. Найдите раСС10Яllllе от сереюtll! >! отрезка до ПЛОСКОСТlI р.

7, На ОJ. ной гpaHII двугранного угла взята TO'lKa j-> и 113 нее ОII)ШС'Н IJСРIJСIIДIIКУ. 1lЯР РН lIa. 1рjТ)Ю грань. paRI! t. III 10 Д\! Найдите расстояние от 1'0'11\11 Р 10 ребра 'lR~ r'j1aHHOI'O ~ I; 1< -1. ce; llt. 1[]~ граJlНЫП угол равен, и^о.

8. На 0. 111011 гp3HII J. вугранного YI" J13 " БОС п]ята точ" а М на раССТОЯННII 5 С, \I ОТ ребра 11 1! 3 нес ОП) щсн пеРПСНDl11\). lЯР М на дp~ 1')'10 111< 1111.. НаiiДllте М,

9. II'i Т()ЧКlt огстояшеil от П. l0С" ОСТl1 на I18ССIШIIIIIII & \1 IIрове. 1еlШ " ПЛОСI\ОСТII на" лонная длшюfi 16м, HailTli ~I'ШI \1СЖ, l) 1I: II\1ОНlюii 11 перпеН. 1l1к~. lЯ~Ю\l,

10. К 11. 'IUCI\Ol" ТlI а проведена наклонная IЮ. J ~ 1': 10\1 ~5. ее прое" UIIЯ на плоскость а раАна 1 1 дм, Наl1Л1 Ш1l! НУ наклонноil. IIРОВI.:,,: {I.: НIЮ(I 1\ плоеКОСТlI И,

(-1; 2; 1)и[

(3; о; 2). Найти вектор -2Ь +

5. 1. Даны вскторы: а = (2; 3; -4), Ь а. - 3[

2. Наiiти )10. 1 ~ЮП) вектораМII а. = -27 + 2} - k 11 Ь -б[ + 3] + бk. з. НUЙПI векторное ЩЮJJЗВСДСIIIIС векторов: а. = [- J + 2k 11 Ь = 2} + k.

векторы: а. = (2; 3; -4), Б = (-1; 2; 1) и [= (3; о; 2). Найти всктор

)(all ы

4ё -2а +Ь

~ (8 5 3) b~ ( 2 8) ~

5, Усл. tll~)В1l" 1е. I{O\1fI. 'IallapHbI ЛII векторы а ;; -1, = -4; ; I с

(4; 7; -4) [c: lIJ век 'ОР'" IIСJ< О\lI'. lаИilРНЫ. ll) какую 01111 образ) ют троНк): " РШI) Ю 11. 111 Jlевуюry

6. Построiiте TO'lKII \[(2: 5: -1) 11 N(--+: 1: 3). [[аЙ.: \lIте КООРДlIнаты Bcкropa МN. ВЫЧИС; lI! ТЬ длнн)' лога всктора.

7. ВЫЯСНII гс. правой '1. 111. 1евоН ЯВ; lяется тройка векторов а

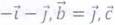
8. Найти объе" IIUР, L1. 1е. 1епнпсда. nOCTpoelllloт на

(-1; 3; 4), [= (2; 5; 2)

а. = (1; 2; 3), Б

Аекторах

'J. [lшlТ11 УГО. 1. \1ежд)' веК'lорами а.

3[- 2] +k и ь = 4[- 7) - 3k

10. lIaiiТII BcкropHOC IIРОIl3ВС. 1ение вскторов а. = 3[- 2} + k и ь = '1·7 - 7} - зk.

6. 1, В УРllе IШХО. 1ЯТСЯ 20 белы: \. 11 15 ЧСРIII, I\ шаРОR Ilа).. 1ач~ ВЫНII\1ают OJIIH шар. KOTOpl. lii ОК, В< L1СЯ бе. 1Ы\1, и откладываЮI сго li сторону, После )того берут еше O.! lllll шар, HaiiTl1 вероятность того. что )10Т шар также окаЖС·IСЯ белым

2. В )pflC lIа\О. 1ЯТСЯ 7 бею. 11(. 11 5 'lepHbIx IШlрОIl, I-I< 1ЙТИ вероятность того. ЧТО два Hay. J. a'I~ выII)'Iы~\( шара окажутся 'lepHbIMII,

3. U )рне на; \ОJЯ IСЯ 10 ()1.:. 11. 1\ 11 () Чt'РJlЫ\ шаров. Hall'! lt В\.. 'Р< ШIIIOСТl. того, что Трll наудачу вынуты\; ОДИН за другим шара окажутся черны'Vtl1,

4. Н ОДlюii ~ рне Нt1\о.. 1ЯТСЯ 4 6е. 1Ы. \ 11 S черВI. IХ IIIЩ)()Н, в лругоfi - 3 белы, It < ) '! ~PHЫ: \.. t 11 каж. JОЙ урны В 1. 11 1) JНI по Ш<. 1r~· Найти верОЯТНОСI ь IОН). что оба Ш< Jра окnжутся белым 11.

5. ВЫЧJIСЛltТlo: а) . 41~ 6) C(~ + ('~)

Экза~I~lIаЦlIонные вопросы 110 M(\Te~taTIIKe 'j(\: 2 семестр

для студентов 1 курса всех специаJll, ностеП на 2013-20 14 уч~бный год

1, 1 I редел фУIIIЩИИ В точке и lIа бесконечноCl'И, ОСНОПIlЫС 'leopeMbI О пре)(еJlах, Неопрсделенности,

') ПРОlIзво: щая, ПОlIятне о ПРОЮВОДIIОЙ ф~ IIKI[HH. её reo~lcl'P" '1cCKHii н фllзическнii CMhIC. l. Ураl3l1еНIl'" ' касательной 11 1I0P~Ia.; 1I1 к графнку (1)\III(1IHI1,

3. ПРОИЗВО. 'lные CY~IМЫ. разНОСТII. произве}tення, чаеТНОI'О двух фУНКЦIIЙ, Таблнца

ПРОИlIЩ'IНhI'С

4, Правнло иссле; ювания фУНКIIИИ на моногонность и JKCTpe~IYM с ПО~IOЩhЮ

" РОIIЗВОДIЮЙ,

5. 1 IrаВИ: 1() IIСС1('. 10ВП! НIЯ ФУНКUIIИ lIa НЫПУК: 1ОСТЬ ВОП-f: TO~TI>. j" ОЧh": 1l переги6а. б, УраНllеНIIЯ аеll\1ПI'ОI,

7, Обшая c\e\la IIССJlсдовання ФУНКЦIIИ С ПО~IOШLЮ " РСНI'JВОДНОЙ, 8, Перпоо6рюная, НСОllре. 'lе. lеНIIЫЙ IIнтеграл 11 его свойства,

9. Та6: lIl11а I! lПСГРа. roв.

10. ОllределеllНLII'1 IIН'lегра. 111 elo своiiстrщ, ФОР~I\'ла НЬЮlона-ЛсiiОlllllll1,

11, ПРIIМСllение опрсдсленного ИНТСГРШIU для наХОЖ)lеНIIЯ плошаДII КРИВОЛИНСЙIIОЙ

трапеЦIIИ,

12, ВзаllМIIОС раСПО, lОЖСНllе!! В\''( ПРЯ~IЫХ в пространстне,

13. ВзаИМllое расположеНllе двух плоскостсй 13 ПРОСlранствс,

14. ВзаЮ1Ное раСПО. lожеНl1е ПРЯ\lОЙ и II, lОСКОСПI В IlpoCTpallcrBe,

15, IlаР3JlЛелыюсть нря~юii 11 ПJЮСКОСТИ, 113ршIлслыlсл,, плоскостеii,

16, ПеРПСIIДНКУJlЯРНОСТЬ прямой н плоскости. Ilcрпендикулярнос I h двух плоскостеii,

17. ПсрпеН. lI1К~: IЯР и lIаК: IOННl1Я. УI'Ш( межд~ нрямоJ1 н П. lОСКОСТЫО, Тсоре~1a о трех пср" е" 1I1Ку. lяра\

lR. Дв: rраllныJj: 'Гоп У! 'О, '! меll\~1У ПJIOСКОСТЯМI1. -[\1НО]" ОгртlllblС )I'Jlbl.

19. ПРС. '1С'13ВJlеНIIС о ПРlll" '. lЫIЫХ \IНОГОГРШIIIIIIШХ (тетрю. 'lР. к" б. ОКТЮ. '1р. }lOдекаэдр и ИКОС~'). tр),

20, ПРIIЗ~lа. IIРЯ\I: IЯ н l/Оh, [()НН({Я ПР" З\1а, ПраВИ. %II8Я " РlIЗма. IIЛОIiLН. 'lЬ ПОВСРХНОСlИ и объем IIРЮМЫ.

21, ПаР3JI. 'lелеПIl ПС)(. К ~ б, ПЛОlll8JLh ПОВСРХII()СТlI И объс'l IIЩХ1Jlлелспи IIС}Щ 11 куба,

22. ПIlРЮlllда, IlраВII. lЫI~И 11I11)< 1\llIда. }'СС'lС/l/lШ/I1l/jJil. \f/lcJа, II. lОIIЩ. 'lh повсрхности 11 объсы

пираМИJlhI,

п, 1 (I1ЛIIНДР, IIЛОIl1Н:: IL повеРХНОСТII 11 объе~1 ЦIIЛИII; tI1Н,

24, Конус, IIЛОIIЩДЬ ПОВСРХНОСТII И объе~1 конуса, Усеченный КОIlУС.

25. Шар 11 с: фера. " х ССЧСНIIЯ, I3заllмное раСПО, 10жеНllе ПЛОСКОСТII 11 шара. Формулы объем~ шара 11 1I10Шl1: 1И сферы.

26, ПРSl\10УГО: IЫJaЯ IдекарlОна) СIIСТС~Ш коорДllllат в IlpocTpallCTl3e. КШlЛлаllарные векторl, l, I'Ш: lOж, 'lIие нектора по I ре. \1!! СКО~IП. шнаРНLШ пектор, ш,

27, ФОР~IРLi. '1ЛЯ H" " IIIC. 1C!! I'" }IJIIIH'" всктора. ) гла ~lеЖ. 'I\' вектора~IИ. расстоянии между

. 'tВУ~IЯ " ]('1ЧI\3\! II. ПРОСКIII! Я псктора на OCI).

28. Скалярное. вскторное 11 СМСIIШННОС ПРОII'ше. 'lеНIIС BCКlOPOB,

29. Уранненис прячой (оОщее. 110 напраЮЯЮЩ" " IУ BCKTOp~'. каНОНllческое).

30. УраВ!! Сllllе IIJЮСКОСl И,

31. OCHoГHII~le IIQIIЯТIIЯ l(or-. ·lбинаТОРI1КJI.

32. СоОI, Пllе. псрОЯ'IIIОСТL собы ПIЯ. К. lаССИ'lеское определеИllе всроятности собhlТIIЯ.

•

12 Следующая ⇒