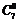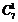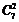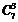- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Біном Нютона. Поліномінальна формула. Принцип включення-виключення
Тема: Біном Нютона. Поліномінальна формула. Принцип включення-виключення
- Поняття біноміальних коефіцієнтів, їх властивості
Біноміальними коефіцієнтами називають числа 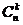
 - кількість комбінацій з n по k,
- кількість комбінацій з n по k,
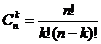 . Властивості біноміальних коефіцієнтів
. Властивості біноміальних коефіцієнтів
1) Нехай n i k – невід’ємні цілі числа, причому 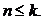 Тоді
Тоді 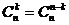
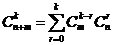 2) Рівність Вандермонда. Нехай n, m, k - невід’ємні цілі числа, причому k≤ min {m, n}
2) Рівність Вандермонда. Нехай n, m, k - невід’ємні цілі числа, причому k≤ min {m, n}
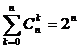 |
Тоді 3)
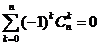 | 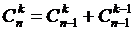 | ||
4) 5) Рівність Паскаля:
Для обчислення біноміальних коефіцієнтів 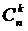 можна використовувати трикутник Паскаля, у якому кожне число (крім одиниць на бічних сторонах) є сумою двох чисел, що стоять над ним.
можна використовувати трикутник Паскаля, у якому кожне число (крім одиниць на бічних сторонах) є сумою двох чисел, що стоять над ним.
| n | |||||||||||||||
| | |||||||||||||||
- Біном Ньютона
Теорема (біноміальна). Нехай х та у – змінні, n – додатне ціле число. Тоді 
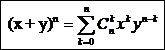
Приклад 1. Знайти 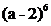 .
.
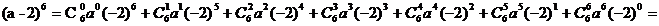
Використовуємо трикутник Паскаля для знаходження 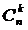
=64+6a(-32)+15a216+20a3(-8)+15a44+6a5(-2)+a6=64-192a+240a2-160a3+60a4-12a5+a6.
- Поліноміальна формула
Як узагальнення бінома Ньютона розглянемо вираз у вигляді 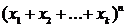
Формула 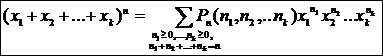 називається поліноміальною.
називається поліноміальною.
Приклад. Знайти 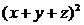
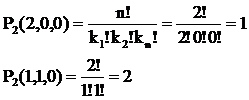

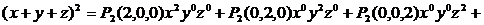
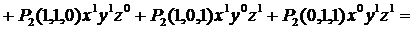
 | |||
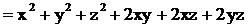 | |||
- Принцип включення-виключення
Цей принцип дає відповідь на запитання, як визначити кількість елементів у об’єднанні множин.
Для двох множин 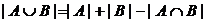
Для трьох множин 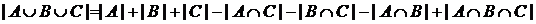
Тема: Біном Нютона. Поліномінальна формула. Принцип включення-виключення
- Поняття біноміальних коефіцієнтів, їх властивості
Біноміальними коефіцієнтами називають числа 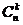
 - кількість комбінацій з n по k,
- кількість комбінацій з n по k,
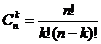 . Властивості біноміальних коефіцієнтів
. Властивості біноміальних коефіцієнтів
2) Нехай n i k – невід’ємні цілі числа, причому 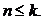 Тоді
Тоді 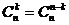
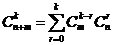 2) Рівність Вандермонда. Нехай n, m, k - невід’ємні цілі числа, причому k≤ min {m, n}
2) Рівність Вандермонда. Нехай n, m, k - невід’ємні цілі числа, причому k≤ min {m, n}
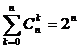 |
Тоді 3)
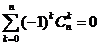 | 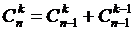 | ||
4) 5) Рівність Паскаля:
Для обчислення біноміальних коефіцієнтів 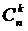 можна використовувати трикутник Паскаля
можна використовувати трикутник Паскаля
n
|
|
|
|
|
|
|
|
| ||||||||
| 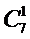
| 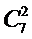
| 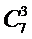
| 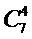
| 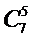
| 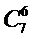
| 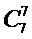
| ||||||||


Теорема (біноміальна). Нехай х та у – змінні, n – додатне ціле число. Тоді 
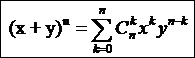
Приклад 1. Знайти 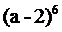
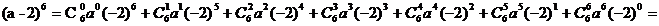
Використовуємо трикутник Паскаля для знаходження 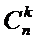
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|