Хелпикс

Главная

Контакты

Случайная статья



Ход урока. Определение



 

 

Тема урока: Компланарные векторы. Правило параллелепипеда.

 

Ход урока

Определение

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны; три вектора, среди которых два коллинеарные, также компланарны.

Пример: рис. 1.

 

 

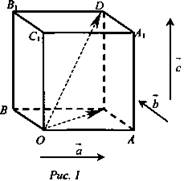
На рис. 1 изображен параллелепипед.

Векторы 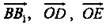- компланарны, так как, если отложить от точки О вектор, равный 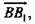то получится вектор 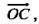а векторы 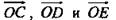лежат в плоскости ОСЕ. 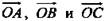- некомпланарны, так как вектор 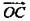не лежит в плоскости ОАВ. Признак компланарности 3-х векторов: если вектор 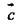можно разложить по векторам 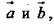то есть представить в виде: 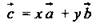(х, у - некоторые числа), то векторы 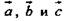- компланарны.

 

 

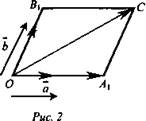
Доказательство: Пусть 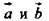не коллинеарные (рис. 2). Отложим отточки О векторы: 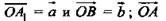и 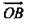лежат в плоскости ОАВ. В плоскости ОАВ лежат и векторы 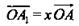и 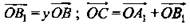лежит в той же плоскости. 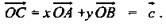Что и требовалось доказать. Обратное утверждение: если векторы 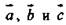компланарны, а векторы 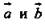некомпланарны, то вектор можно разложить по векторам 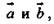то есть 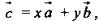причем коэффициенты х и у определяются единственным образом.

Доказательство: на основании теоремы о разложении вектора по двум неколлинеарным векторам.

1) 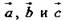- компланарны (по условию).

Если их отложить от точки А, то они будут лежать в одной плоскости.

2) Построим параллелограмм ABCD: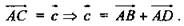

3) 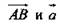коллинеарные 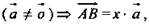аналогично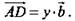

4) 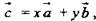что и требовалось доказать (единственность коэффициентов х, у доказать самостоятельно дома).

 

Правило параллелепипеда (для сложения трех некомпланарных векторов).

Дано: 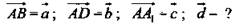(рис. 3).

 

 

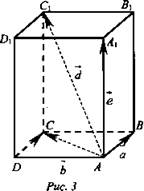
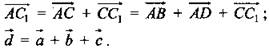
Задача.

Дано: 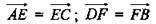(рис. 4).

 

 

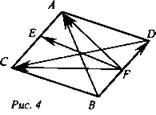
1) Доказательство: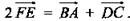

2) 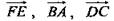- компланарны -?

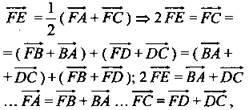
согласно признаку компланарности, векторы 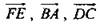компланарны.

Решение упражнений № 359 a)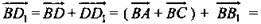

 



  

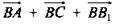
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.