Призма. Площадь поверхности призмы

Мы с вами приступили к изучению новой большой главы: «Многогранники». Тема нашего сегодняшнего урока: «Призма». Мы поговорим о видах призм, познакомимся с понятием площади поверхности призмы, с теоремой о площади боковой поверхности прямой призмы и затем рассмотрим задачи.

Призма является многогранником. С какими многогранниками мы уже знакомы?

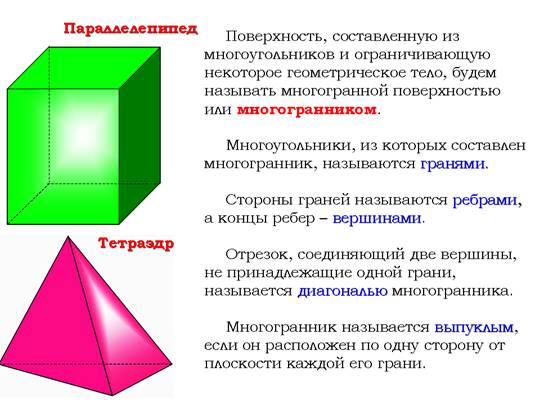
Призма тоже многогранник. Значит, в первую очередь, что мы будем понимать под призмой?

Какие элементы можно выделить у призмы?

Основания, боковые грани, вершины, ребра.

Теперь нам нужно разобраться, из каких именно многоугольников составлена поверхность и сколько их. У призмы 2 основания, основаниями являются два равных многоугольника, которые лежат в параллельных плоскостях, а остальные грани, боковые, – параллелограммы. Их столько, сколько и углов у многоугольника в основании.

Определение призмы

Призмой называется многогранник, составленный из двух равных многоугольников, лежащих в параллельных плоскостях, и параллелограммов

Рассмотрим два равных многоугольника А₁А₂…А_n и В₁В₂…В_n, расположенных в параллельных плоскостях α и β так, что отрезки А₁В₁, А₂В₂…А_nB_n, соединяющие соответственные вершины многоугольников, параллельны. Каждый из n четырехугольников А₁А₂В₂В₁, А₁А₂В₂В₁, …А_nА₁В₁В_n является параллелограммом.

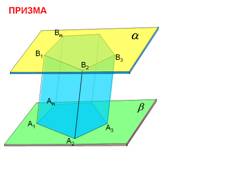
Мы получили Призму.

МногоугольникиА₁А₂…А_n и В₁В₂…В_n называются основаниями, а А₁А₂В₂В₁, А₁А₂В₂В₁, …А_nА₁В₁В_n – боковыми гранями призмы, а отрезки А₁В₁, А₂В₂…А_nB_n – ее боковыми ребрами.

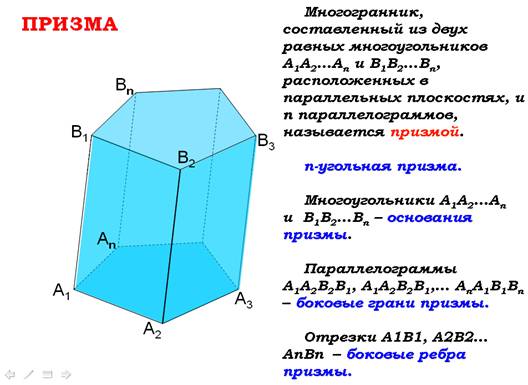
Призму с основаниями А₁А₂…А_n и B₁B₂…B_n обозначают А₁А₂…А_nВ₁В₂В_n и называют n-угольной призмой.

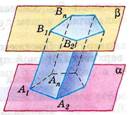
А₁А₂…А_nВ₁В₂В_n – _призма_ Многоугольники А₁А₂…А_n и В₁В₂…В_n – _основания призмы_ Параллелограммы А₁А₂В₂В₁, А₁А₂В₂В₁, …А_nА₁В₁В_n – _боковые грани Отрезки А₁В₁, А₂В₂…А_nB_n – _боковые ребра призмы_

Запишем определение высоты призмы

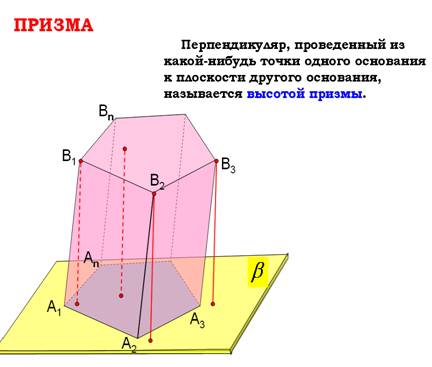
2. Виды призм: прямая, наклонная правильная

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.

Рассмотрим примеры призм.

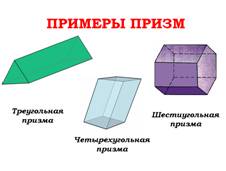
Название призмы зависит от того, какие многоугольники лежат в её основаниях: треугольники – треугольная призма, пятиугольники – пятиугольная и т. д. Четырёхугольная призма является параллелепипедом.

призма будет называться правильной если ее основания – правильные многоугольники.

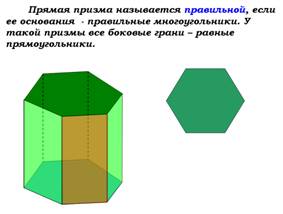
Но изначально эта призма ещё должна быть прямой. У такой призмы все боковые грани являются равными прямоугольниками. Запишите это в свои бланки.

3. Формирование понятия площадей полной и боковой поверхностей призмы.

Площадь полной поверхности призмы состоит из площадей оснований и площади боковой поверхности.

Площадью полной поверхности призмы называется сумма площадей всех ее граней (т. е. основания и боковых граней), а площадью боковой поверхности призмы – сумма площадей ее боковых граней. Площадь полной поверхности выражается через площадь боковой поверхности и площадь основания призмы формулой:

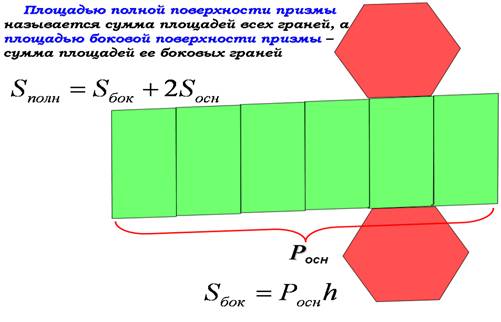
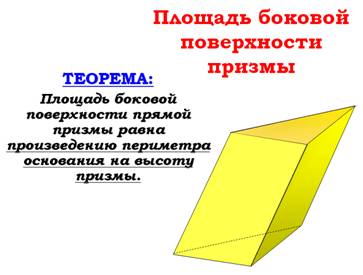
Формулировка теоремы звучит так: «Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы». Это выражается формулой: S_бок = Ph.

решение задач.

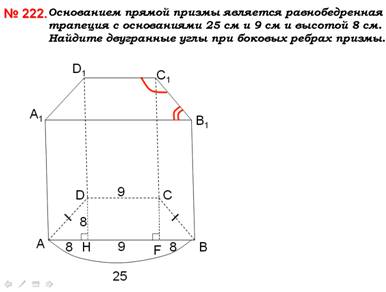
№ 222. Основанием прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 см и высотой 8 см. Найдите двугранные углы при боковых ребрах призмы.

Дано: АВСDA₁В₁C₁D₁ – прямая призма, ABCD –трапеция, AD = BC, АВ = 25, СD = 9, DH = 8. Найти: Ð А₁В₁C₁ и Ð В₁C₁D₁ (Ð АВC и Ð ВCD).

Домашнее задание.

§1, стр 67 №219 уч-к Атанасян 10 класс.

Задача: В прямоугольном параллелепипеде стороны основания равны 12см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 45 градусов. Найти боковое ребро параллелепипеда.