
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Метод интервалов:. Корни и степени. Показательные уравнения, неравенства. Логарифмические уравнения, неравенства. Прямые и плоскости в пространстве. Сделать чертёж. Записать символически, что в теореме дано и что нужно доказать
Метод интервалов:
1. 
2. 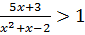
Иррациональные уравнения:
1. 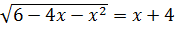
2. 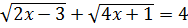
3.  ;
;
Методом замены переменной (тоже много будет примеров)
4. 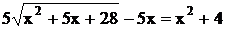
5. 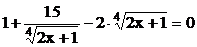
Иррациональные неравенства:
1. 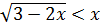
2. 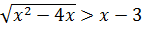
3. 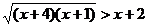
Корни и степени
1. 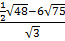
2. 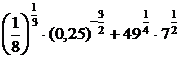
Показательные уравнения, неравенства. Логарифмические уравнения, неравенства
1. Решить уравнения:
1. 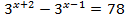 ; 2.
; 2. 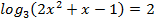 ;
;
3. 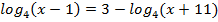 4.
4. 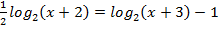 ;
;
5. 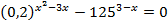 6.
6. 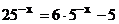
7. 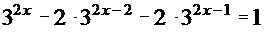 ; 8.
; 8. 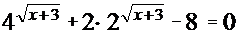 ;
;
9. 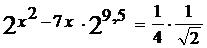 ; 10.
; 10. 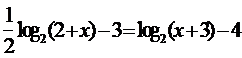 ;
;
11. 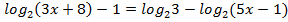 12.
12. 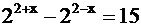
13. 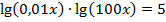
4. Решить неравенства:
1. 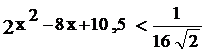 ; 2.
; 2. 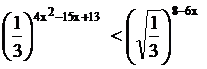 ;
;
3.  4.
4. 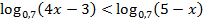
5. 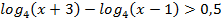
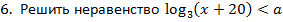 , где а – наибольшее значение переменной у, удовлетворяющей системе уравнений:
, где а – наибольшее значение переменной у, удовлетворяющей системе уравнений: 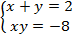
Прямые и плоскости в пространстве
¨ Закончите формулировку теоремы: Прямая, проведённая в плоскости перпендикулярна наклонной, когда она …
А) параллельна проекции этой наклонной.
B) перпендикулярна проекции этой наклонной.
С) скрещивается с проекцией этой наклонной.
Сделать чертёж. Записать символически, что в теореме дано и что нужно доказать
♦ Задан куб ABCDA1B1C1D1. Построить угол отрезка A1M с гранью A1B1C1D1, где М – середина ребра DC. Записать определение угла между прямой и плоскостью.
1. Стороны D-ка равны 51 см, 30 см и 27 см. Из вершины меньшего угла этого D-ка проведён перпендикуляр к его плоскости, равный 10 см. Вычислить расстояние от концов перпендикуляра до противолежащей стороны треугольника.
2. Точка А равноудалена от вершин правильного треугольника со стороной 18 и находится на расстоянии 5 от его плоскости. Вычислить расстояние от точки А до а) вершин треугольника; б) до сторон треугольника.
3. Плоскости равнобедренного DADM и прямоугольника ABCD взаимно перпендикулярны. Вычислить расстояние между вершинами М и С, если у треугольника AM=MD=6, Ð M=1200, у прямоугольника диагональ равна 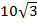 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|