Энтропия.

Энтропия – величина, которая показывает число способов расположения частиц в пространстве и распределения их по энергиям.

Мысленный эксперимент. Пролили бензин в дальнем углу гаража. Что произойдет и почувствуем ли мы запах бензина при открывании дверей? Имеет ли место диффузия? Возможна диффузия при отсутствии воздуха?

Возьмем две емкости объединенные перегородкой. Поместим в одну из них несколько молекул бензина( пусть 5).

Емкость1 Емкость2

Емкости без воздуха. Откроем перегородку. Что произойдет? Имеет ли место хаотичность движения?

Вероятность молекуле бензина остаться в емкости 1: 1 / 2⁵=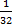

Вывод: молекулы диффундируют вследствие того, что способов расположения во всем объеме больше, чем когда они находятся все только в одном месте.

Понятие « число возможных вариантов или способов» важно: оно определяет, насколько вероятны изменения в системе.

Идея такова: события, которые происходят, имеют наибольшую вероятность произойти. Чем больше возможных вариантов дл того, чтобы события могли произойти, тем, больше вероятность того, что оно произойдет.

Почему смешиваются жидкости?

Опыт: в стакан положите слой арахиса и слой кешью (месяцеобразный). Встряхните. Что произойдет? Можно ли вернуть в первоначальное состояние? Только теоретически.

Вывод: жидкости смешиваются потому, что число возможных способов их смешивания больше, чем способов разделения.

Но так происходит не всегда. Пример: вода + бензин. Почему? Сила взаимодействия между молекулами каждой из жидкостей больше сил взаимодействия воды и бензина. Поэтому расслаиваются. Сравните эмульсию воды в нефти при стабилизаторах – смолы + асфальтены (битум + минеральные вещества). Её даже разрушают центрифугированием, повышением температуры и направленным действием электрического поля.

Общее правило смешивания: вещества стремятся перемешаться, если не существует сил противодействия.

Таким образом, число способов очень важно для определения того, как происходит изменение в системе.

Для химической системы (реагент – продукт) изменения в системе характеризуются энтропией.

Используется для оценки химических процессов изменение энтропии, а не абсолютное ее значение. Обозначается Δ S. При Δ S> 0 процесс протекает, а при Δ S< процесс по энтропии не разрешен. [S]=Дж/ моль·К.

Сравним стандартную молярную энтропию S⁰ для некоторых веществ:

Вещество	S⁰ Дж/ моль·К.	Вещество	S⁰ Дж/ моль·К.
Н₂О_лед		алмаз	2. 4
Н₂О_{жидкость}		СН₄	186. 2
Н₂О_газ	188. 7	С₃Н₆	229. 9

Закономерность изменения энтропии:

1. у газов энтропия > чем у жидкости > чем у твердых веществ.

2. вещества со сложной структурой имеют энтропию > чем простые вещества.

3. алмаз – одна из самых правильных и совершенных структур природы. Энтропия минимальная.

Тренировочные упражнения:

1. Для каких процессов энтропия уменьшается, увеличивается, остается постоянной?

Процесс	S⁰ Дж/ моль·К.: ↑, ↓, const
Испарение бензина	↑
Конденсация паров бензина	↓
Растворение сахара в воде	↑
Смешивание масла с бензином	↑
Разделение суспензии масла в воде на два слоя	const
Эмульсия природной нефти с водой	const

2. Какие вещества обладают большей энтропией и почему?

-твердый воск или расплавленный воск.

-бром жидкий или бром газообразный

-отдельные образцы меди и цинка или латунь (их сплав)

-пентан С₅Н₁₂или октан С ₈Н₁₈?

Первый закон термодинамики позволяет предсказать изменения в системе и окружающей среде при отсутствии на самом деле самих процессов.

Второй закон термодинамики дает ответы на такие вопросы, как: какими законами определяются самопроизвольность течения термодинамических процессов? Можно ли предсказать направления самопроизвольных процессов? При каких условиях процессы протекают полнее? Какая работа будет получена при этом? и т. д.

Второй закон термодинамики имеет несколько формулировок:

1. Невозможен процесс, единственным результатом которого было бы превращение теплоты в работу (постулат Томсона).

2. Невозможен самопроизвольный переход теплоты от холодного тела к горячему (постулат Клаузиуса).

3. Невозможно построить такую машину (вечный двигатель второго рода), все действия которой сводились бы к производству работы и соответствующему охлаждению теплового источника. Всякая машина производит работу только при наличии разности температур между теплоотдатчиком (Т₁) и теплоприемником (Т₂). (первый постулат Планка).

4. Любая форма энергии может полностью преобразовываться в теплоту, но теплота преобразуется в другие виды энергии лишь частично (второй постулат Планка).

Самая ранняя формулировка второго закона термодинамики, появилась раньше первого начала, связана с работами С. Карно.

КПД машины = (Т₁–Т₂)/Т₁

В основном реакции протекают, если Δ Н< 0. Но известно, что самопроизвольно идут реакции, сопровождающиеся увеличением энтальпии и охлаждением реактора (эндотермические). Для характеристики таких реакций введена новая функция – энтропия. Обозначается S. Измеряется ее изменение Δ S. [S]=Дж/моль·К.

Изменение энтропии равно минимальной теплоте, подводимой к системе в обратном изотермическом процессе, деленной на абсолютную температуру процесса: Δ S=Q_мин/ T.

Открытая система	Изолированная система dQ=0
Самопроизвольный процесс Δ S> Q_мин/ T. Равновесный процесс Δ S=Q_мин/ T. Несамопроизвольный процесс Δ S< Q_мин/ T.	Самопроизвольный процесс Δ S> 0. Равновесный процесс Δ S= 0. Несамопроизвольный процесс Δ S< 0.

В общем случае Δ S ≥ 0 (процесс протекает или находится в состоянии равновесия). Δ S ≥ Q_мин/ T. Это неравенство Клаузиуса. Аналитическое выражение второго закона термодинамики.

Существуют две точки зрения на применимость второго закона термодинамики.

Не применим к системам с небольшим числом частиц, космическим системам, живым объектам как открытым системам. Почему? Теряется смысл для систем с малым числом частиц. Вселенная неравновесная и стремится к однородному изотермическому состоянию (энтропия стремится к максимуму, тепловая смерть Вселенной). Живые системы способны к самосозиданию (автопоэз). Сами удаляются от классического динамического равновесия и делают еще неравновесной окружающую среду.

На этом подходе американец Джеймс Лавлок в 1965г. предложил в качестве критерия наличия жизни на Марсе оценивать равновесность состава атмосферы.

Земля, температура +40-(-50) º С	Марс, температура +20 – (-125) º С, среднесуточная -60 º С.
Кислород 21% Азот 78% Метан 0. 00018% Водород 0. 00005% Монооксид углерода СО 0. 00001% Углекислый газ СО₂0. 035%	Углекислый газ СО₂95% Кислород 1% Метан (восстановитель) не обнаружен.
Смесь газов неравновесна. Земная атмосфера – открытая система, в формировании которой постоянно участвуют живые организмы. Т. е. жизнь присутствует.	Атмосфера Марса равновесна, все реакции между газами уже осуществились. В настоящее время жизни на Марсе нет.

Согласно другой точки зрения: Вселенная постоянно расширяется (вещества в ней рассредотачиваются), а также под действием сил тяготения происходит скопление веществ: звезд, планет, галактик и т. д. Все эти процессы идут в строгой согласованности с законами термодинамики.

Тоже и для живых объектов. Открытые живые системы на определенных временах можно рассматривать как квазизакрытые ( без постороннего вмешательства) по отношению к процессам, для которых устанавливаются локальные равновесия. Каждую неравновесную систему можно разбить на бесконечно малые объемы, что их неоднородностью можно пренебречь. Каждый малый объем неравновесной системы в любой момент времени находится в состоянии равновесия.

Игнорировать второй закон термодинамики равносильно тому, чтобы не прочесть ни строчки Шекспира.

«Энтропия – стрела времени». Эддисон.

«Выигрыш в информации – это проигрыш в энтропии». Льюис.

«Выигрыш в энтропии – выигрыш в идиотизме».

Второй закон термодинамики предсказывает вероятность события и причину его свершения.

- Нельзя дважды войти в одну и ту же воду.

-Нельзя ничего вернуть в первоначальное состояние.

Задача 1. Возможно ли образование сероводорода H₂S из простых веществ при стандартных условиях по энтропии?

Химическая реакция: Н_{2 (Г)}+ S_(к) → H₂S_(г)Справочник: cтандартные абсолютные энтропии

Н_{2 (Г)} =+130. 5Дж/ К·моль S_(к)=+31. 9 Дж/ К·моль

H₂S_(г)= + 205, 7 Дж/ К·моль

Решение: Δ S⁰_{реакции} = 205. 7 – (130. 5 +31. 9) = 205. 7 – 162. 4 =43. 3( Дж/ К·моль) > 0 Процесс возможен.

Задача 2. С точки зрения изменения энтропии оцените возможность протекания процесса:

1вариант 2 вариант

Н₂О _(ж)→ Н₂О _(п) С_графит→ С_алмаз

Справочник: Н₂О _(ж)=70. 1 Дж/ К·моль Н₂О _(п)=188. 7 Дж/ К·моль С_графит=5. 7 Дж/ К·моль С_алмаз =2. 3 Дж/ К·моль

Решение: (записать самостоятельно! ).

Ответ: 118. 6 Дж/ К·моль, возможен; -3. 4 Дж/ К·моль, невозможен.

Задача 3. Оценить возможность самопроизвольного процесса Н₂О _(ж)→ Н₂О _(тв) при t=-10º C и t=+10º C.

Справочные данные:

Вещество	Δ Н⁰, кДж/моль	Δ S⁰, Дж/ К·моль
Н₂О _(ж) Н₂О _(тв)	-285. 84 -291. 85

Δ Н⁰_{х. р.}= -291. 85 – (-285. 84) = -6. 01( кДж/моль) < 0, процесс возможен.

Δ S⁰_{х. р.} = 48-70 = -22(Дж/ К·моль) < 0, процесс невозможен.

Δ S_{окр. среды}= - Δ Н / T и Δ S_общ.= Δ S⁰_{х. р.}+ Δ S_{окр. среды}

При температуре +10 º C: Δ S_{окр. среды}= - (6010Дж/моль): (273+10) = -21. 2 Дж/ К·моль

Δ S_общ.= 22 +(-21. 2) =+0. 8 Дж/ К·моль > 0 Процесс возможен. Самопроизвольный.

При температуре -10 º C: Δ S_{окр. среды}= - (-6010Дж/моль): (273-10) = +22. 9 Дж/ К·моль

Δ S_общ.=- 22 +22. 9) =+0. 9 Дж/ К·моль > 0 Процесс возможен. Самопроизвольный.

Задание:

Вычислить значение энтропии при стандартных условиях для той реакции, для которой вы рассчитывали энтальпию в предыдущем задании. Предоставить расчет к 16 декабря.