
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Гиперболическая спираль. Гиперболическая спираль в жизни
Гиперболическая спираль
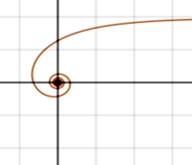
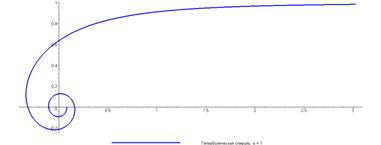
Гиперболическая спираль — плоская трансцендентная кривая. Уравнение гиперболической спирали в полярной системе координат является обратным для уравнения Архимедовой спирали и записывается так:
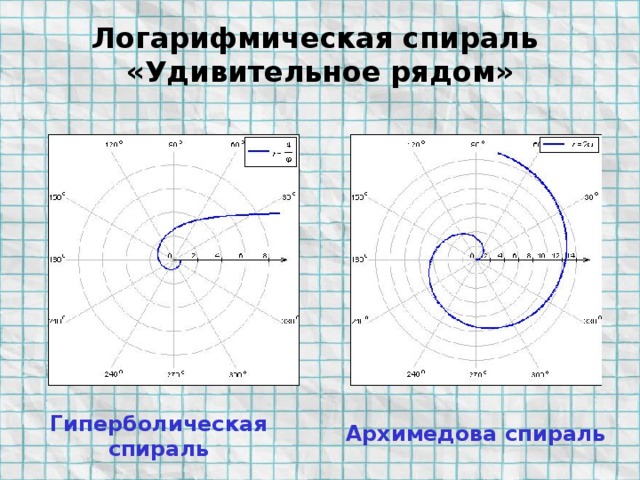
ρ φ = a
Кривая состоит из двух ветвей, симметричных относительно прямой. Начало координат является асимптотической точкой. Асимптота - прямая, параллельная полярной оси и отстоящая от нее на расстоянии.
Гиперболическая спираль получается при движении точки по вращающейся прямой таким образом, что ее расстояние от центра вращения всегда будет обратно пропорционально углу поворота прямой, измеренному от начального положения.
Найдем площадь сектора:
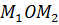
Итак,
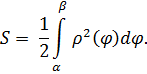
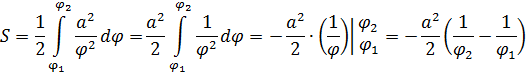
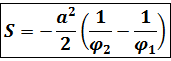
Вычислим длину дуги гиперболической спирали, используя формулу:
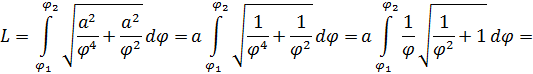
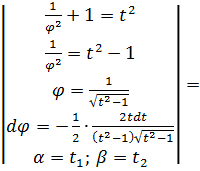
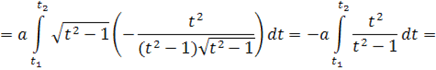
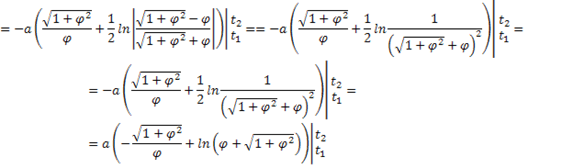
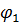
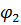
Итак, длина дуги между точками M1(, ) и M2(, ) имеет вид:
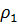
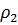
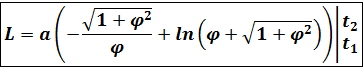
Уравнение гиперболической спирали в декартовых координатах:

Параметрическая запись уравнения:
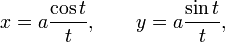
Спираль имеет асимптоту y = a: при t стремящемся к нулю ордината стремится к a, а абсцисса уходит в бесконечность:
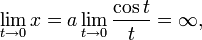
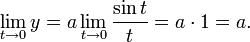
Гиперболическая спираль в жизни

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|