Вид сырья. Нормы расхода сырья на единицу продукции. Запасы

Вариант 10

1. Провести полное исследование и построить график функции

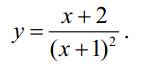
Полное исследование функции оформить в текстовом документе. Построение графика выполнить в электронных таблицах, сделать скриншот и перенести его в текстовый документ, подписать как рисунок. На графике функции в электронных таблицах отметить и подписать точки максимума и минимума функции, точки перегиба функции. При наличии асимптот построить их на одном изображении вместе с графиком и подписать.

Решение:

1. (X+1)²≠ 0 => x ≠ -1 => область определения функции

X ∈ (-∞; -1) ⋃ (-1; +∞ )

2. В текстовом документе построить математическую модель задачи линейной оптимизации: ввести переменные, записать к ним комментарии, записать целевую функцию, указать направление ее оптимизации, записать систему ограничений. Решить задачу линейной оптимизации с помощью средств MS Excel (надстройка Поиск решения), сделать скриншоты решения в электронных таблицах и перенести их в текст, подписать как рисунки.

Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цена реализации единицы каждого вида продукции приведены в таблице:

Вид сырья	Нормы расхода сырья на единицу продукции			Запасы сырья
Вид сырья	А	Б	В	Запасы сырья
Труд
Сырьё 1
Сырьё 2
Оборудование
Цена единицы продукции				-

В ответе записать оптимальный план производства продукции и размер максимальной выручки, которую можно получить при этом

Решение:

Обозначим через x_1,x₂, x₃число трех видов сырья.

f(X) = 6x₁+10x₂+9x₃

Ограничения по ресурсам:

3x₁+6x₂+4x₃ ≤ 2000

20x₁+15x₂+20x₃ ≤ 15000

10x₁+15x₂+20x₃ ≤ 7400

3x₂+5x₃≤ 1500

Введем исходные данные. Сначала опишем целевую функцию с помощью функции СУММПРОИЗВ, а потом введем данные для левых частей ограничений. В Поиске решения введем направление целевой функции, адреса искомых переменных, добавим ограничения. На экране появится диалоговое окно Поиск решения с введенными условиями (рис. 1)

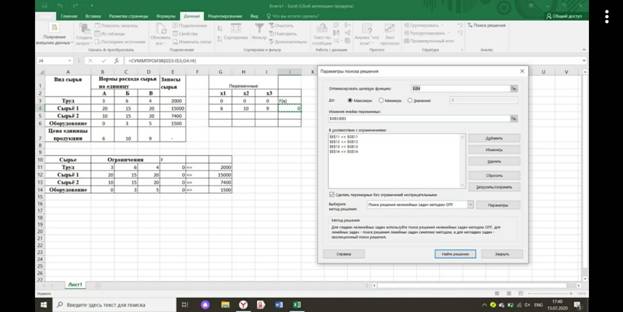
1. Введены все условия задачи

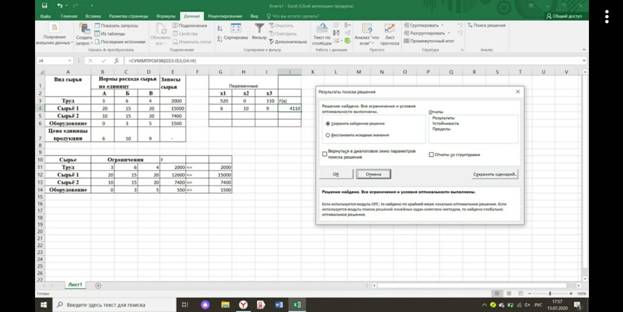
Рис. 2. 2

Полученное решение означает

12 Следующая ⇒