Учитель: Жабаев Еркасым Классы: 9 Б. 9В.

Дата: 18. 09. 18-20. 09. 18

Учитель: Жабаев Еркасым Классы: 9 Б. 9В.

Тема урока. §7 Равномерное движение тела по окружности. Период и частота вращения. Угловая скорость

Цель: формировать знания о перемещение, путь, скорость и ускорение, о направление мгновенной скорости во время криволинейного движения, период и частоту вращения тела; сравнить перемещение, путь, скорость во время прямолинейного равномерного, неравномерного и криволинейного движений; рассказать о широкое применение криволинейных движений в технике, сельском хозяйстве.

Тип урока: урок изучения нового учебного материала.

Наглядный: демонстрация криволинейных движений, движения по кругу, направления мгновенной скорости во время криволинейного движения

ХОД УРОКА

I. Актуализация опорных знаний

Фронтальное опрос о траектория, путь, перемещение, мгновенную скорость прямолинейного движения.

II. Мотивация обучения. Сообщение темы и задач урока

III. Изучение нового материала

В ходе эвристической беседы ученики, слушая учителя, выполняют рисунки в тетрадях, делают записи.

Простейшим видом криволинейного поступательного движения тела является его движение по кругу, когда все точки тела движутся по одинаковым кругах. Такое движение встречается довольно редко: так двигаются кабинки смотровых колес в городских парках. В то же время любое сложное криволинейное движение тела на достаточно малом участке его траектории можно приближенно рассматривать как равномерное движение по окружности. Поэтому изучать произвольное криволинейное движение надо начинать от простого: изучение равномерного движения по окружности. Примерами равномерного движения по окружности можно приближенно считать: движение искусственных спутников Земли, движение вращающихся частей в механизмах и т. д.

Начнем изучение этого движения с важной кинематической величины мгновенной скорости. Мгновенная скорость в любой точке криволинейной траектории движения тела направлена по касательной к траектории в этой точке.

Положение точки A, что движется вдоль круга, определяют радиус-вектором 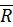, проведенным из центра окружности O до этой точки (рис. 1). Модуль радиуса-вектора равна радиусу этого круга R.

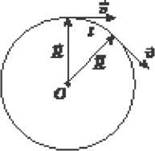
Рис. 1

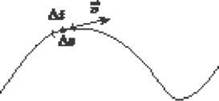
Рис. 2

Скорость движения тела по окружности (линейную скорость) по аналогии с равномерным прямолинейным движением можно найти по формуле:

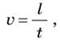
где l - длина дуги круга, пройденного материальной точкой за время t (рис. 2).

Пусть тело совершит один оборот по окружности, тогда формула для определения скорости примет вид.