
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
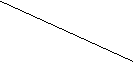
Число называется сопряженным числу . Геометрически эти числа симметричны относительно оси ОХ. (рис. 4.)
I Комплексные числа
1. Комплексные числа, геометрическое изображение, форм их задания.
Комплексным числом называется выражение вида 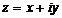 , где x и y – действительные числа; i – мнимая единица
, где x и y – действительные числа; i – мнимая единица 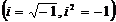 ;
;
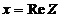 – действительная часть комплексного числа;
– действительная часть комплексного числа;
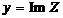 – мнимая часть комплексного числа.
– мнимая часть комплексного числа.
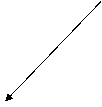
Комплексное число 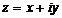 изображается на плоскости хОу, которую будем называть комплексной плоскостью, точкой М (х, у) или радиусом-вектором
изображается на плоскости хОу, которую будем называть комплексной плоскостью, точкой М (х, у) или радиусом-вектором 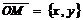 . Модуль обозначается через
. Модуль обозначается через 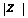 и вычисляется по формуле
и вычисляется по формуле
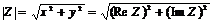 (1)
(1)
Аргумент комплексного числа 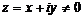 - угол между радиусом-вектором точки, изображающей комплексное число на плоскости, и осью абсцисс – обозначается ArgZ.
- угол между радиусом-вектором точки, изображающей комплексное число на плоскости, и осью абсцисс – обозначается ArgZ.
Главным значением аргумента называется угол, лежащий в промежутке 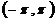 , обозначается argZ (далее
, обозначается argZ (далее 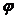 ).
).
Аргумент и его главное значение связаны следующим соотношением:

 ,
, 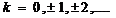 (2)
(2)
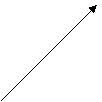
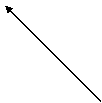
Главное значение аргумента Z определяется по формуле (см. рис. 1)
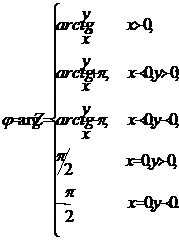 (3)
(3)
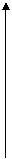
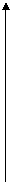 y y
y y

 M (x, y)
M (x, y)


 x
x

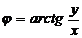
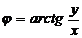

 x M (x, y)
x M (x, y)
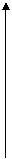


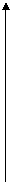 y
y
y


 M (x, y)
M (x, y)
 x
x

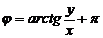


 x M (x, y)
x M (x, y)
Рис. 1
Действительная и мнимая части комплексного числа выражаются через модуль и аргумент следующим образом
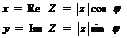 (4)
(4)
Формы задания комплексных чисел:
алгебраическая:
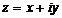 ; (5)
; (5)
тригонометрическая:
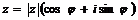 ; (6)
; (6)
показательная:
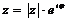 . (7)
. (7)
Типовые примеры.
Записать заданные комплексные числа в различных формах. Изобразить числа геометрически, найти 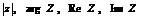 . Указать их на чертеже.
. Указать их на чертеже.
1. 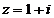
Решение:
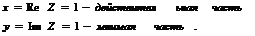
Модуль 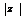 найдем по формуле (1)
найдем по формуле (1)
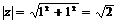
Аргумент числа найдем по формуле (3) учитывая, что 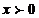
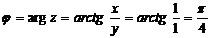 .
.
Запишем комплексное число в тригонометрической форме по формуле (6)
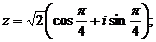
в показательной форме по формуле (7)
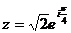
Изобразим число 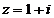 на рис. 2 как точку плоскости с координатами (1, 1)
на рис. 2 как точку плоскости с координатами (1, 1)
y


 1 M (1, 1)
1 M (1, 1)
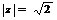
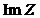

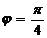
0  1 x
1 x
Рис. 2.
2. 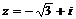
Решение
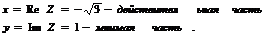
Модуль 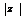 найдем по формуле (1)
найдем по формуле (1)
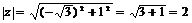
Аргумент числа найдем по формуле (3) учитывая, что 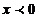 ,
, 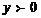
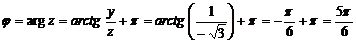 .
.
Комплексное число 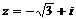 в тригонометрической форме по формуле (6)
в тригонометрической форме по формуле (6)
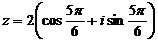 ,
,
в показательной форме по формуле (7)
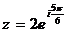 .
.
Комплексное число 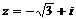 изобразим на рис. 3 как точку
изобразим на рис. 3 как точку 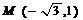 .
.
 у
у


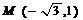 1
1
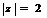



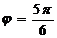

 -2
-2 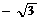 -1 0 х
-1 0 х
Рис. 3.
Контрольное задание.
Записать комплексное число в алгебраической, тригонометрической, показательной формах; найти модуль и аргумент; изобразить геометрически
1. 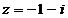 ; 2.
; 2. 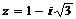 ; 3.
; 3. 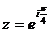 ; 4.
; 4. 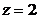 ;
;
5. 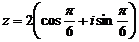 ; 6.
; 6. 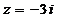 .
.
2. Действия над комплексными числами, заданными в алгебраической форме.
Два комплексных числа 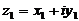 и
и 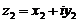 равны между собой тогда и только тогда, когда равны между собой их вещественные и мнимые части.
равны между собой тогда и только тогда, когда равны между собой их вещественные и мнимые части.
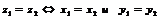 .
.
Очевидно, что равны их модули и аргументы  .
.
Суммой чисел 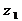 и
и 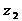 называется комплексное число
называется комплексное число
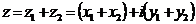 ,
,
а их разностью – комплексное число
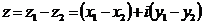 .
.
При сложении (или вычитании) комплексных чисел векторы складываются (или вычитаются) по правилам векторной алгебры.
При умножении комплексных чисел пользуются правилом умножения двучленов, учитывая, что 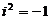 .
.
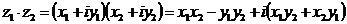 (8)
(8)
Число называется сопряженным числу. Геометрически эти числа симметричны относительно оси ОХ. (рис. 4. )
 |
y


 z
z

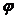

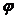 х
х

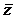
Рис. 4.
Очевидно, что 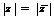 ,
, 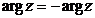 .
.
Сопряженное число в показательной форме имеет вид 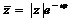 .
.
Произведение комплексного числа на ему сопряженное равно квадрату его модуля:
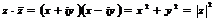 (9)
(9)
При делении комплексных чисел 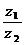 необходимо числитель и знаменатель дроби умножить на число, сопряженное знаменателю:
необходимо числитель и знаменатель дроби умножить на число, сопряженное знаменателю:
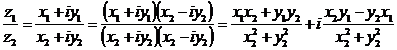 (10)
(10)
Запоминать формулы (8), (10) нет необходимости, так как операции производятся как с обычными многочленами, учитывая только, что
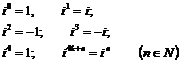
Типовые примеры.
Даны 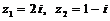
Найти: 1) 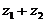 ; 2)
; 2) 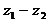 ; 3)
; 3) 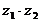 ; 4)
; 4) 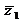 и
и 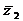 ; 5)
; 5) 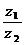 ; 6)
; 6) 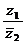 .
.
Решение:
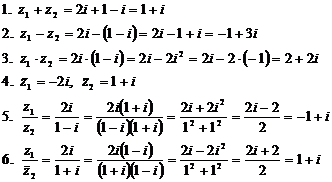
Контрольное задание.
7. Даны 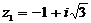 ,
, 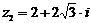
Найти: 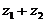 ;
; 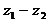 ;
; 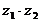 ;
; 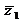 и
и 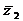 ;
; 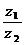 ;
; 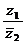 .
.
3. Действия над комплексными числами, заданными в тригонометрической и показательной формах.

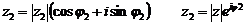
Сложение и вычитание комплексных чисел рекомендуется проводить в алгебраической форме.
При умножении двух комплексных чисел их модули перемножаются, а аргументы складываются, т. е.
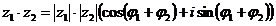 (11)
(11)
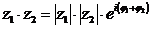 (12)
(12)
При делении двух комплексных чисел их модули делятся, а аргументы вычитаются.
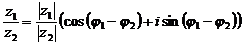 (13)
(13)
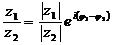 (14)
(14)
При возведении в степень модуль возводится в ту же степень, а аргумент умножается на показатель степени
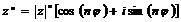 (15)
(15)
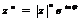 (16)
(16)
Формула (16) известна как формула Муавра. В частности,
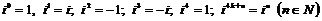 .
.
Извлечение корня п-ой степени производится по формуле
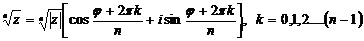 (17)
(17)
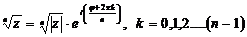 (18)
(18)
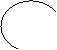
В результате извлечения корня п-ой степени получают п различных значений комплексных корней (т. е. п разных комплексных чисел), модули которых равны 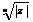 , а аргументы двух соседних чисел отличаются на постоянное число
, а аргументы двух соседних чисел отличаются на постоянное число 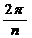 . В связи с этим все корни п-ой степени лежат на одной окружности радиуса
. В связи с этим все корни п-ой степени лежат на одной окружности радиуса 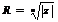 в вершинах правильного п- угольника.
в вершинах правильного п- угольника.
Типовые примеры.
Даны 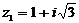 ,
, 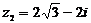
Найти: 1) 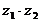 ; 2)
; 2) 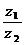 ; 3)
; 3) 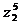 ; 4)
; 4) 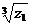 .
.
Решение:
Запишем 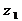 и
и 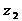 в тригонометрической форме
в тригонометрической форме
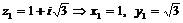
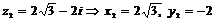
По формуле (1) найдем модули чисел
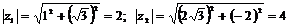 .
.
По формуле (3) найдем аргументы 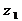 и
и 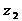
т. к. 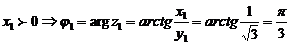
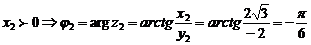
Согласно формуле (6), имеем
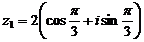
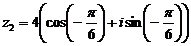 .
.
1. Найдем 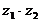 по формуле (11)
по формуле (11)
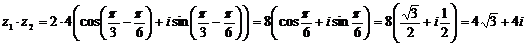
2. Найдем 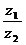 по формуле (12)
по формуле (12)
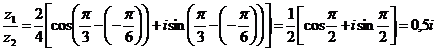
3. Используя формулу (15), получим
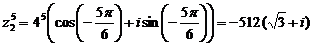
4. Согласно формуле (17), имеем
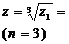
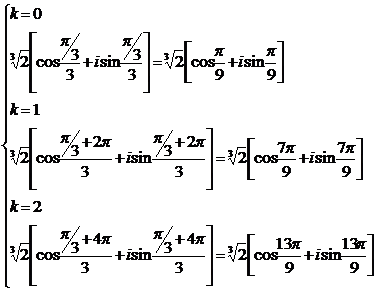
Представим значения комплексных корней на рис. 5
 y
y

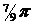




 z1
z1 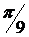

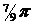

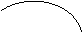


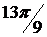 z0
z0
 x
x
z2
Рис. 5
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|