
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
«КОМПЛЕКСНЫЕ ЧИСЛА». Геометрическое изображение комплексного числа
Опорный конспект №1-Спо теме
«КОМПЛЕКСНЫЕ ЧИСЛА»
Опр.: Комплексным называется число вида 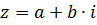 , где
, где 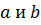 - заданные действительные числа,
- заданные действительные числа, 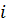 - специальный символ, называемый « мнимой единицей » и обладающий свойством
- специальный символ, называемый « мнимой единицей » и обладающий свойством 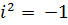 . Число
. Число 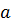 называется действительной частью комплексного числа, а число
называется действительной частью комплексного числа, а число 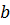 - мнимой частью. Обозначают: a=Re(z), b= Im(z).
- мнимой частью. Обозначают: a=Re(z), b= Im(z).
Например: z=2+5i(здесь 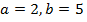 ), z=-4-i(здесь
), z=-4-i(здесь 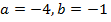 ), z= 7i(здесь
), z= 7i(здесь 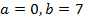 )
)
Существует три формы записи комплексных чисел:
1) 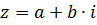 - алгебраическая форма комплексного числа
- алгебраическая форма комплексного числа
2) 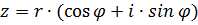 – тригонометрическая форма комплексного числа, где
– тригонометрическая форма комплексного числа, где
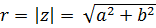 - модуль,
- модуль, 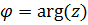 - аргумент комплексного числа
- аргумент комплексного числа
(cos 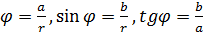 ).
).
3) 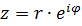 - показательная форма (экспонента е≈ 2. 7).
- показательная форма (экспонента е≈ 2. 7).
Опр.: Два комплексных числа называются равными, если равны соответственно их действительные и мнимые части.
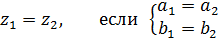
Опр.: Комплексное число равно нулю, если его действительная и мнимая части равны нулю. 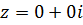 .
.
Опр.: Два комплексных числа называются сопряженными, если их действительные части равны, а мнимые - противоположны. Обозначают 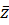 – сопряженное к z.
– сопряженное к z.
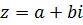 ,
, 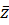 =
= 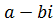 .
.
Геометрическое изображение комплексного числа
Комплексные числа изображают на комплексной плоскости в виде точки с координатами ( 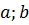 ), то есть, по оси Ох откладывают действительную часть комплексного числа, а по оси Оу – мнимую часть, или изображают в виде вектора с началом в начале координат и концом в точке (
), то есть, по оси Ох откладывают действительную часть комплексного числа, а по оси Оу – мнимую часть, или изображают в виде вектора с началом в начале координат и концом в точке ( 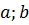 ).
).
Опр.: Модулем комплексного числа называется длина вектора, соответствующего комплексному числу: 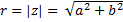 .
.
Опр.: Аргументом комплексного числа называется угол между положительным направлением действительной оси и вектором, соответствующим комплексному числу. (Обозначается 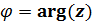 . Вычисляется cos
. Вычисляется cos 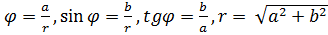 )
)
Опр.: Главнымаргументом комплексного числа называется наименьшее по абсолютной величине значение его аргумента. (Обозначается 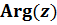 .
. 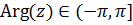 . )
. )
Операции над комплексными числами.
Над комплексными числами можно выполнять все 6 видов операций:
1) сложение, 2) вычитание, 3) умножение, 4) деление, 5)возведение в степень, 6) извлечение корня
Нельзя только сравнивать (т. е. сказать, какое число больше, а какое меньше).
Складывать и вычитать комплексные числа удобнее в алгебраической форме записи. Умножать и делить можно во всех формах записи. Возводить в степень и извлекать корень лучше в тригонометрической форме.
Пусть 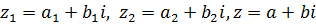 - комплексные числа в алгебраической форме,
- комплексные числа в алгебраической форме, 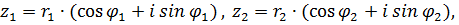
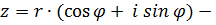 тригонометрическая форма этих чисел.
тригонометрическая форма этих чисел.
Тогда имеют место следующие формулы:
1. Сложение 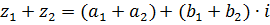
Чтобы сложить два комплексных числа надо сложить между собой их действительные части и сложить их мнимые части.
2. Вычитание 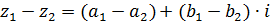
Чтобы найти разность двух комплексных чисел надо из действительной части уменьшаемого вычесть действительную часть вычитаемого, а из мнимой части уменьшаемого вычесть мнимую часть вычитаемого.
3. Умножение 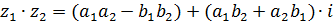
Чтобы найти произведения двух комплексных чисел в алгебраической форме надо из произведения действительных частей вычесть произведение мнимых частей, а сумму попарных произведений действительной на мнимую части домножить на 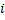 .
.
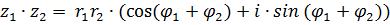
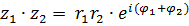
Чтобы найти произведения двух комплексных чисел в тригонометрической форме надо их модули перемножить, а аргументы сложить.
4. Деление 
Чтобы найти частное двух комплексныхчисел 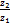 надо числитель и знаменатель дроби домножить на число, сопряженное знаменателю.
надо числитель и знаменатель дроби домножить на число, сопряженное знаменателю.
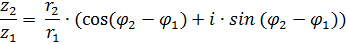
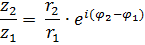
Чтобы найти частное двух комплексныхчисел 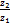 в тригонометрической форме надоих модули разделить (модуль делимого разделить на модуль делителя), а аргументы вычесть.
в тригонометрической форме надоих модули разделить (модуль делимого разделить на модуль делителя), а аргументы вычесть.
5. Возведение в степень 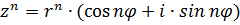 , n – натуральное число.
, n – натуральное число.
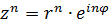
Чтобы возвести комплексное число в степень надо модуль данного числа возвести в эту степень, а аргумент умножить на показатель степени.
Квадрат комплексного числа вычисляется по формуле:
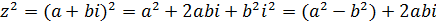
6. Извлечение корня
Опр.: Число z называется корнем n-ой степени из комплексного числа w, если оно является решением уравнения 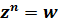 .
.
Пусть комплексные числа z и w представлены в своей тригонометрической форме 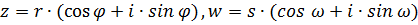
Уравнение вида 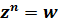 имеет
имеет 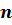 разных решений, вычисляемых по формуле:
разных решений, вычисляемых по формуле: 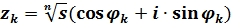 , где
, где 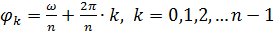 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|