Контакты

Случайная статья

Тема. Подвійний інтеграл та його застосування.

⇐ ПредыдущаяСтр 2 из 2

Завдання №1. Обчислити інтеграли

1. 1.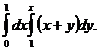

1. 2.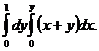

1. 3.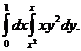

1. 4.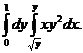

1. 5.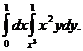

1. 6.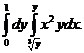

1. 7.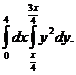

1. 8.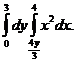

1. 9.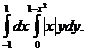

1. 10.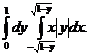

1. 11.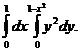

1. 12.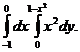

1. 13.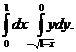

1. 14.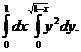

1. 15.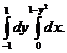

1. 16.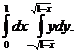

1. 17.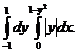

1. 18.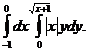

1. 19.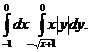

1. 20.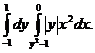

1. 21.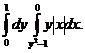

1. 22.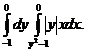

1. 23.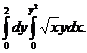

1. 24.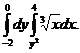

1. 25.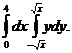

Завдання №2. Змінити порядок інтегрування.

2. 1.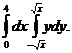

2. 2.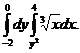

2. 3.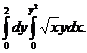

2. 4.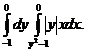

2. 5.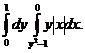

2. 6.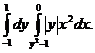

2. 7.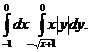

2. 8.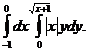

2. 9.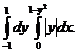

2. 10.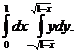

2. 11.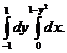

2. 12.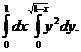

2. 13.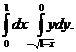

2. 14.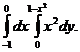

2. 15.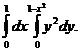

2. 16.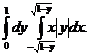

2. 17.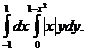

2. 18.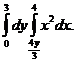

2. 19.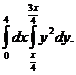

2. 20.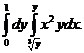

2. 21.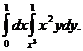

2. 22.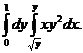

2. 23.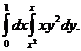

2. 24.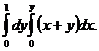

2. 25.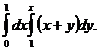

Завдання №3. Обчислити інтеграл.

3. 1.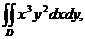

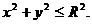
3. 2.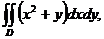

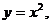
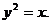
3. 3.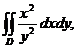

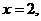
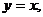
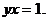
3. 4.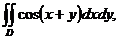

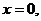
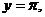
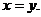
3. 5.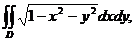

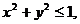
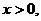
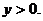
3. 6.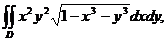

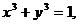
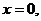
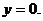
3. 7.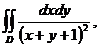

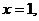
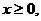
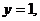
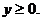
3. 8.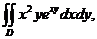

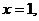
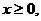
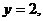
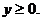
3. 9.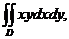

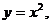
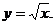
3. 10.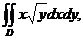

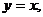
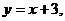
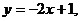
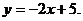
3. 11.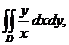

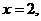
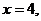
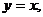
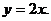
3. 12.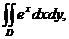

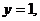
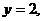
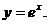
3. 13.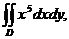

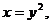
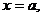
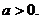
3. 14.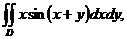

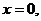
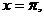
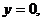
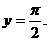
3. 15.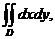

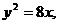
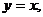
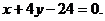
3. 16.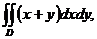

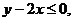
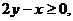
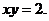
3. 17.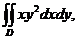

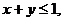
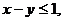
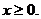
3. 18.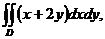

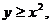
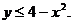
3. 19.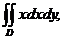

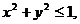
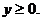
3. 20.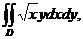

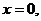
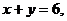
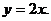
3. 21.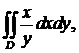

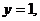
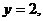
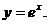
3. 22.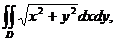

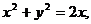
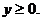
3. 23.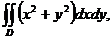

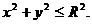
3. 24.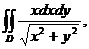

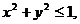
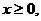
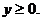
3. 25.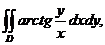

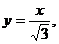
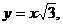
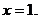
3. Змінити порядок інтегрування.

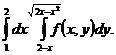
Розв’язання.

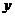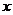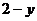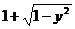При зміні від 0 до 1 змінюється в області інтегрування від до , отже одержимо повторний інтеграл

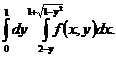
4. Обчислити інтеграл.

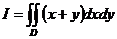, де область 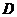обмежена кривими , , .

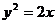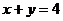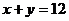Розв’язання.

Пряма 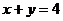і парабола 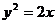перетинаються в точках з абсцисами 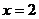і 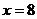, а пряма 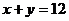і парабола 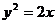перетинаються в точках з абсцисами 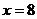і 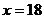, тому область інтегрування можна представити у вигляді об'єднання замкнутих областей , .

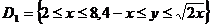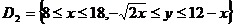Переходячи від подвійного інтеграла до повторного, одержуємо:

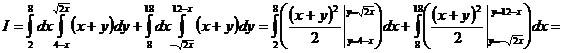
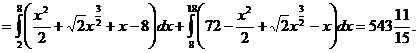
3. Змінити порядок інтегрування.

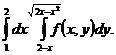(Двойной, поверхностный? )

Розв’язання.

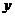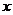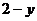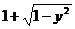При зміні від 0 до 1 змінюється в області інтегрування від до , отже одержимо повторний інтеграл

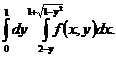
4. Обчислити інтеграл.

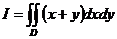, де область 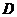обмежена кривими , , .

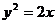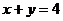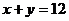Розв’язання.

Пряма 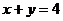і парабола 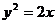перетинаються в точках з абсцисами 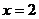і 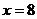, а пряма 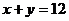і парабола 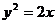перетинаються в точках з абсцисами 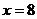і 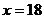, тому область інтегрування можна представити у вигляді об'єднання замкнутих областей , .

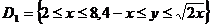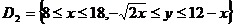Переходячи від подвійного інтеграла до повторного, одержуємо:

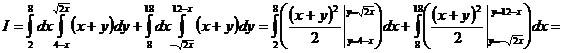
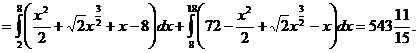
Найти площадь области, ограниченной кривыми:

1. №9. 4(5)

2. №9. 4(4)

3. №9. 4(3)

4. №9. 4(2)

5. №9. 4(1)

6. №9. 4(6)

7. №9. 4(7)

8. №9. 4(8)

9. №9. 4(9)

10. №9. 6(1)

11. №9. 6(2)

12. №9. 6(3)

13. №9. 6(4)

14. №9. 6(5)

15. №9. 6(6)

16. №9. 6(7)

17. №9. 7(1)

18. №9. 7(2)

19.

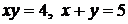
20.

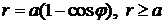
Найти объем тела, ограниченного поверхностями:

1. №9. 12(5)

2. №9. 12(4)

3. №9. 12(3)

4. №9. 12(2)

5. №9. 12(1)

6. №9. 12(6)

7. №9. 12(7)

8. №9. 12(8)

9. №9. 12(9)

10. №9. 13(2)

11. №9. 13(1)

12. №9. 13(3)

13. №9. 14(1)

14. №9. 14(2)

15. №9. 14(3)

16. №9. 14(4)

17. №9. 14(5)

18. №9. 16(1)

19. №9. 16(2)

20. №9. 16(3)

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.