Проекции прямого угла

Любой линейный угол проецируется на плоскость в натуральную величину, если его стороны параллельны этой плоскости. Прямой угол проецируется в натуральную величину еще и тогда, когда только одна из его сторон параллельна плоскости проекций, а вторая – не перпендикулярна к ней.

Теорема 1. Если одна сторона прямого угла параллельна плоскости проекций, а другая является прямой общего положения, то прямой угол проецируется на эту плоскость без искажения, т. е. в прямой угол. Докажем это.

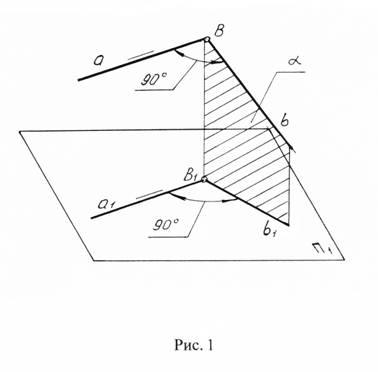
Пусть прямые a и b образуют прямой угол и прямая a параллельна плоскости П₁ (рис. 1). Так как прямая a перпендикулярна прямой b (по условию) и ВВ₁ (по построению), то, следовательно, она перпендикулярна плоскости α . Поскольку прямая a и ее проекция a₁ параллельны между собой, то прямая a₁ также перпендикулярна к плоскости α , а значит и к прямой b₁.

Аналогично можно доказать, что если ортогональная проекция угла является прямым углом и одна его сторона параллельна плоскости проекций, то этот угол – прямой.

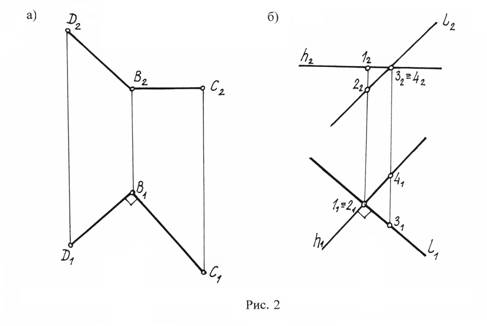
На чертеже (рис. 2) показаны проекции прямого угла DBC, сторона ( BC ) которого параллельна плоскости П₁ (рис. 2, а), и проекции взаимно перпендикулярных скрещивающихся прямых, одна из которых является горизонталью (рис. 2, б).

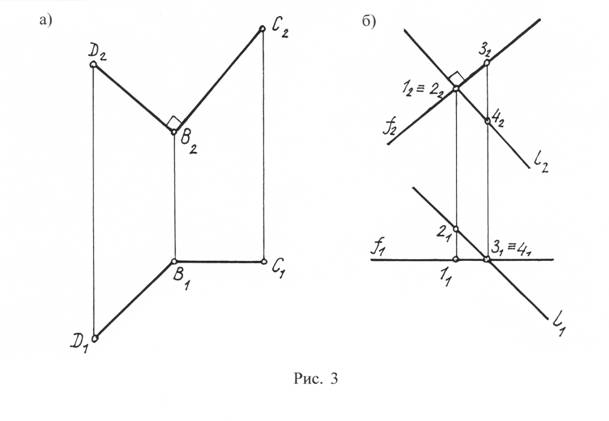
На рисунке 3, а изображены проекции прямого угла DBC, сторона ( BC ) которого параллельна плоскости П₂, а на рисунке 3, б – проекции взаимно перпендикулярных скрещивающихся прямых, одна из которых является фронталью.