
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Домашняя работа 1
1. Килограмм орехов стоит 75 рублей. Маша купила 4 кг 400 г орехов. Сколько рублей сдачи она должна получить с 350 рублей?
2. Поезд Казань-Москва отправляется в 21: 35, а прибывает в 10: 35 на следующий день (время московское). Сколько часов поезд находится в пути?
4. Таксист за месяц проехал 6000 км. Стоимость 1 литра бензина — 20 рублей. Средний расход бензина на 100 км составляет 9 литров. Сколько рублей потратил таксист на бензин за этот месяц?
5. Летом килограмм клубники стоит 80 рублей. Мама купила 1 кг 200 г клубники. Сколько рублей сдачи она получит с 500 рублей?
7. На счету Машиного мобильного телефона было 53 рубля, а после разговора с Леной осталось 8 рублей. Сколько минут длился разговор с Леной, если одна минута разговора стоит 2 рубля 50 копеек?
8. Выпускники 11а покупают букеты цветов для последнего звонка: из 3 роз каждому учителю и из 7 роз классному руководителю и директору. Они собираются подарить букеты 15 учителям (включая директора и классного руководителя), розы покупаются по оптовой цене 35 рублей за штуку. Сколько рублей стоят все розы?
9. Показания счётчика электроэнергии 1 ноября составляли 12 625 кВт·ч, а 1 декабря — 12 802 кВт·ч. Сколько нужно заплатить за электроэнергию за ноябрь, если 1 кВт·ч электроэнергии стоит 1 рубль 80 копеек? Ответ дайте в рублях.
10. Маша отправила SMS-сообщения с новогодними поздравлениями своим 16 друзьям. Стоимость одного SMS-сообщения 1 рубль 30 копеек. Перед отправкой сообщения на счету у Маши было 30 рублей. Сколько рублей останется у Маши после отправки всех сообщений?
13. На автозаправке клиент отдал кассиру 1000 рублей и залил в бак 28 литров бензина по цене 28 руб. 50 коп. за литр. Сколько рублей сдачи он должен получить у кассира?
15. В квартире, где проживает Алексей, установлен прибор учёта расхода холодной воды (счётчик). 1 сентября счётчик показывал расход 103 куб. м воды, а 1 октября — 114 куб. м. Какую сумму должен заплатить Алексей за холодную воду за сентябрь, если цена 1 куб. м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.
16. Рост человека 6 футов 1 дюйм. Выразите его рост в сантиметрах, если 1 фут равен 12 дюймам. Считайте, что 1 дюйм равен 2, 54 см. Результат округлите до целого числа сантиметров.
17. Бегун пробежал 50 м за 5 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
18. В книге Елены Молоховец «Подарок молодым хозяйкам» имеется рецепт пирога с черносливом. Для пирога на 10 человек следует взять 1/10 фунта чернослива. Сколько граммов чернослива следует взять для пирога, рассчитанного на 3 человек? Считайте, что 1 фунт равен 0, 4 кг.
19. Система навигации самолёта информирует пассажира о том, что полёт проходит на высоте 37 000 футов. Выразите высоту полёта в метрах. Считайте, что 1 фут равен 30, 5 см.
20. Стоимость полугодовой подписки на журнал составляет 460 рублей, а стоимость одного номера журнала — 24 рубля. За полгода Аня купила 25 номеров журнала. На сколько рублей меньше она бы потратила, если бы подписалась на журнал?
21. В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 10% от стоимости купленной мебели. Шкаф стоит 3300 рублей. Во сколько рублей обойдётся покупка этого шкафа вместе со сборкой?
22. На бензоколонке один литр бензина стоит 32 руб. 60 коп. Водитель залил в бак 30 литров бензина и купил бутылку воды за 48 рублей. Сколько рублей сдачи он получит с 1500 рублей?
23. Установка двух счётчиков воды (холодной и горячей) стоит 3300 рублей. До установки счётчиков за воду платили 800 рублей ежемесячно. После установки счётчиков ежемесячная оплата воды стала составлять 300 рублей. Через какое наименьшее количество месяцев экономия по оплате воды превысит затраты на установку счётчиков, если тарифы на воду не изменятся?
Упражнение 2
1. 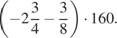 2.
2. 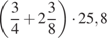 . 3.
. 3.  4.
4. 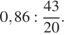
5. 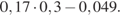 6.
6. 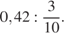 7.
7. 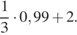 8..
8.. 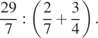 10.
10.  11.
11. 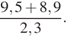 12.
12. 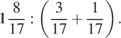 13.
13. 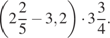 15.
15. 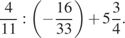
16. 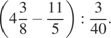 17.
17.  19.
19. 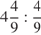 . 20.
. 20. 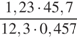 . 21.
. 21. 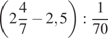 . 22.
. 22. 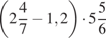 . 23.
. 23. 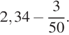 24.
24. 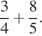 25.
25. 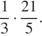 26.
26. 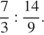 27.
27. 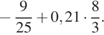
28. 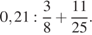 29.
29. 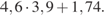 30
30 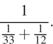 31.
31. 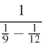 . 32.
. 32. 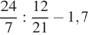 .
.
33. 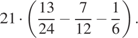 34.
34. 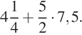 35.
35. 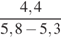 . 36.
. 36. 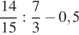 . 37.
. 37.  38.
38. 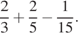 39.
39. 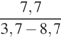 . 40.
. 40. 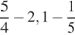 . 41.
. 41. 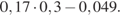 42.
42. 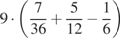 .
.
Упражнение 3
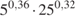

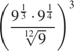
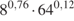 .
. 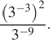
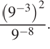
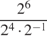
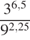
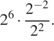
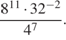
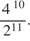
 4 · 72 + 6 · 72.
4 · 72 + 6 · 72. 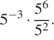
4 · 10-3 + 8 · 10-2 + 5 · 10-1. 9 · 10-2 + 4, 5 · 10-1. (0, 01)2 · 105: 4− 2 3, 4 · 102 + 1, 8 · 103. . 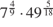 .
. 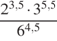 .
. 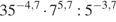 .
. 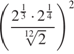 .
. 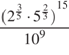 . .
. . 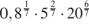 .
. 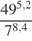 .
. 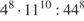
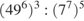
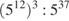
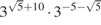
.
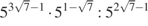 .
. 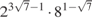 .
. 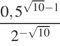 .
. 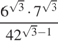 .
. 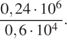
34. 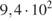 +
+ 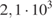 35. 36. 1, 6 · 102 * 4 · 10− 2. 37.
35. 36. 1, 6 · 102 * 4 · 10− 2. 37. 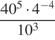 .
. 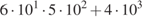
38. 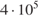 +
+ 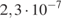 . 39.
. 39. 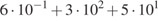 .
. 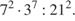 42.
42. 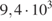 +
+ 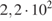 .
.

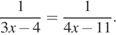
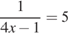
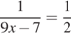
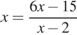
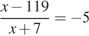
 .
. 
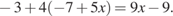 : .
: . 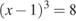
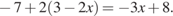 .:
.: 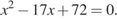 .
.  .
. 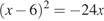 .
. 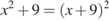 .
. 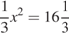 .
. 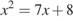 .
. 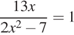 .
. 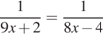
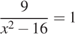
: . . .
Упражнение 4
7. В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
8. Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
10. Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 20 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
11. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
15. Клиент А. сделал вклад в банке в размере 7700 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал клиент Б. Еще ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на 847 рублей больше клиента Б. Какой процент годовых начислял банк по этим вкладам?
16. Имеется два сосуда. Первый содержит 100 кг, а второй — 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 72% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 78% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
21По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
25. Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 4, 4 км от дома. Один идёт со скоростью 2, 5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от дома произойдёт их встреча? Ответ дайте в километрах.
17. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
18. Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
1. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
2. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
3. Из пункта A круговой трассы выехал велосипедист. Через 30 минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч..
4. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
5. Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.
4. На пост главы администрации города претендовало три кандидата: Журавлёв, Зайцев, Иванов. Во время выборов за Иванова было отдано в 2 раза больше голосов, чем за Журавлёва, а за Зайцева — в 3 раза больше, чем за Журавлёва и Иванова вместе. Сколько процентов голосов было отдано за победителя?
5. Первый сплав содержит 5% меди, второй — 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава.
6. Свежие фрукты содержат 80% воды, а высушенные — 28%. Сколько сухих фруктов получится из 288 кг свежих фруктов?
8. Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
16. Имеются два сосуда, содержащие 48 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 42% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 40% кислоты. Сколько килограммов кислоты содержится во втором растворе?
17. Смешали некоторое количество 21-процентного раствора некоторого вещества с таким же количеством 95-процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
18. Свежие фрукты содержат 93% воды, а высушенные — 16%. Сколько сухих фруктов получится из 252 кг свежих фруктов?
Упражнение 5
2. Задание 4 № 506276. Среднее геометрическое трёх чисел 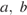 и
и  вычисляется по формуле
вычисляется по формуле 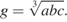 Вычислите среднее геометрическое чисел 12, 18, 27.
Вычислите среднее геометрическое чисел 12, 18, 27.
4. Задание 4 № 506294. В фирме «Эх, прокачу! » стоимость поездки на такси (в рублях) рассчитывается по формуле 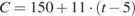 , где
, где  — длительность поездки, выраженная в минутах
— длительность поездки, выраженная в минутах  . Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
. Пользуясь этой формулой, рассчитайте стоимость 8-минутной поездки.
5. Задание 4 № 506295. Площадь параллелограмма 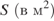 можно вычислить по формуле
можно вычислить по формуле 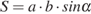 , где
, где 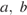 — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и
— стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и 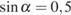 .
.
6. Задание 4 № 506296. Длину окружности 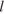 можно вычислить по формуле
можно вычислить по формуле 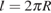 , где
, где 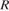 — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать
— радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать  ).
).
8. Задание 4 № 506298. Площадь треугольника 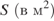 можно вычислить по формуле
можно вычислить по формуле 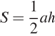 , где
, где  — сторона треугольника,
— сторона треугольника, 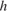 — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону
— высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону  , если площадь треугольника равна
, если площадь треугольника равна 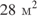 , а высота
, а высота 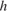 равна 14 м.
равна 14 м.
13. Задание 4 № 506303. Площадь треугольника можно вычислить по формуле 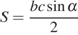 , где
, где 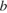 и
и  — стороны треугольника, а
— стороны треугольника, а  — угол между этими сторонами. Пользуясь этой формулой, найдите площадь треугольника, если
— угол между этими сторонами. Пользуясь этой формулой, найдите площадь треугольника, если  = 30°,
= 30°,  = 5,
= 5, 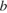 = 6.
= 6.
14. Задание 4 № 506304. Площадь треугольника можно вычислить по формуле  , где
, где  — длины сторон треугольника,
— длины сторон треугольника,  — радиус вписанной окружности. Вычислите длину стороны
— радиус вписанной окружности. Вычислите длину стороны  , если
, если 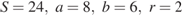 .
.
15. Задание 4 № 506305. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой F = 1, 8C + 32, где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует − 1° по шкале Цельсия?
16. Задание 4 № 506306. Площадь любого выпуклого четырехугольника можно вычислять по формуле 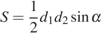 , где
, где 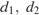 — длины его диагоналей, а
— длины его диагоналей, а  угол между ними. Вычислите
угол между ними. Вычислите 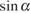 , если
, если  .
.
17. Задание 4 № 506307. Центростремительное ускорение при движении по окружности (в м/c2 ) можно вычислить по формуле 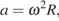 где
где 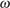 — угловая скорость (в с− 1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с− 1, а центростремительное ускорение равно 45 м/c2.
— угловая скорость (в с− 1), а R — радиус окружности. Пользуясь этой формулой, найдите расстояние R (в метрах), если угловая скорость равна 3 с− 1, а центростремительное ускорение равно 45 м/c2.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|