
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Некоторые виды интегрируемых дифференциальных уравнений
1. Простейшее дифференциальное уравнение имеет вид у′ = f(х). Смысл формулы Ньютона – Лейбница состоит в том, что решением этого уравнения является интеграл 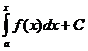 . Именно по примеру этого простейшего случая принято называть решения дифференциальныхуравнений интегралами.
. Именно по примеру этого простейшего случая принято называть решения дифференциальныхуравнений интегралами.
Пример. Решить уравнение y′ = sin x. Очевидно, что y = – соs x + С.
2. Уравнения с разделяющимися переменными называются уравнения вида 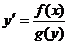 . Учитывая, что
. Учитывая, что 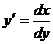 можно записать это же уравнение в виде f(x) dx = g(y) dy.
можно записать это же уравнение в виде f(x) dx = g(y) dy.
Предположим, что решением такого уравнения является заданная неявно функция F(x, y) = C. Продифференцируем её и получим выражение 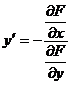 . Имея ввиду равенство
. Имея ввиду равенство 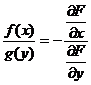 , можно предположить, что
, можно предположить, что 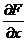 зависит только от х, а
зависит только от х, а 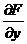 зависит только от у. Можно догадаться, что функция F(x, y) имеет вид F1(x) + F2(y). Если это так, мы имеем два равенства
зависит только от у. Можно догадаться, что функция F(x, y) имеет вид F1(x) + F2(y). Если это так, мы имеем два равенства 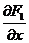 = f(x) и
= f(x) и 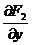 = – g(y), которые позволяют найти функции F1(x) и F2(y). Очевидно, что
= – g(y), которые позволяют найти функции F1(x) и F2(y). Очевидно, что 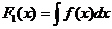 и
и 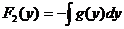 . В итоге формула решения уравнения с разделяющимися переменными имеет вид
. В итоге формула решения уравнения с разделяющимися переменными имеет вид 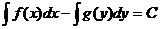 .
.
Формально процедуру решения уравнения с разделяющимися переменными можно представить как интегрирование левой и правой частей равенства f(x) dx = g(y) dy. При этом каждая часть равенства интегрируется по своей переменной: 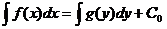 .
.
Пример. Решить уравнение x y dx + (x + 1) dy = 0. Проведём разделение переменных, т. е. преобразуем уравнение к виду 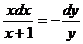 . Отсюда следует, что решение имеет вид
. Отсюда следует, что решение имеет вид 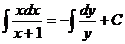 . Интегрируя, получаем следующее решение: х – ln (x + 1) = – ln y + C (при этом используется тот факт, что
. Интегрируя, получаем следующее решение: х – ln (x + 1) = – ln y + C (при этом используется тот факт, что 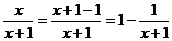 ). Преобразуя, получаем х – C = ln (х + 1) – ln у или
). Преобразуя, получаем х – C = ln (х + 1) – ln у или 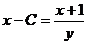 . Окончательно,
. Окончательно, 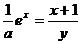 , где
, где 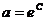 .
.
В итоге можно задать решение в явном виде 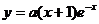 . Кроме того, мы делили обе части уравнения на х + 1. В результате потеряно решение х = – 1.
. Кроме того, мы делили обе части уравнения на х + 1. В результате потеряно решение х = – 1.
3. Однородные уравнения имеют вид 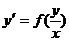 и сводятся к уравнениям с разделяющимися переменными с помощью замены переменных y = t x. Дифференцируя получаем равенство dy = t dx + x dt. Отсюда следует, что
и сводятся к уравнениям с разделяющимися переменными с помощью замены переменных y = t x. Дифференцируя получаем равенство dy = t dx + x dt. Отсюда следует, что 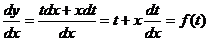 или
или 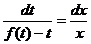 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|