Хелпикс

Главная

Контакты

Случайная статья



Жоғары математика 5 страница

⇐ ПредыдущаяСтр 5 из 9Следующая ⇒


D) 3

E)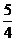

$$$28 Е

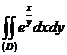 - ті табың дар, мұ ндағ ы D: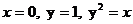

А) 1, 5

В)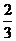

С)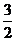

D) 2

E)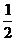

$$$29 С

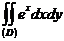 - ті табың дар, мұ ндағ ы D: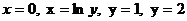

А) 1, 5

В)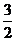

С)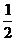

D) 2

E)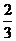

$$$30 D

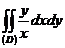 - ті табың дар, мұ ндағ ы D:

А) 7

В) 8

С) 10

D) 9

E) 6

$$$31 А

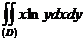 - ті табың дар, мұ ндағ ы D: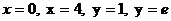

А) 8

В)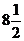

С) 9

D) 10

E) 7

$$$32 D

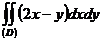 - ті табың дар, мұ ндағ ы D: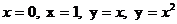

А) 1

В) 3

С) 0, 8

D) 0, 1

E) 0, 2

$$$33 С

 - ті табың дар, мұ ндағ ы D: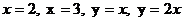

А) 20

В) 24

С)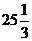

D)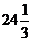

E) 0

$$$34 В

Поляр координаталарына кө шу арқ ылы 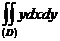  интегралын есептең дер, мұ ндағ ы D:  болса.

А) 0, 1

В)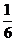

С)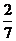

D)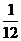

E)

$$$35 С

Поляр координаталарына кө шу арқ ылы 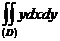  интегралын есептең дер, мұ ндағ ы D:  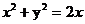болса.

А)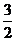

В)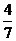

С)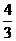

D)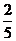

E)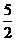

$$$36 В

Поляр координаталарына кө шу арқ ылы 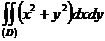  интегралын есептең дер, мұ ндағ ы D:  болса.

А)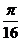

В)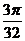  

С)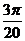  

D)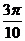  

E)

$$$37 В

Поляр координаталарына кө шу арқ ылы 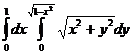 интегралын есептең дер.

А)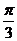  

В)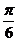

С)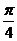

D)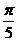

E)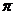

$$$38 C

Поляр координаталаына кө шу арқ ылы  интегралын есептең дер

A)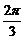

B)

C)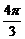

D)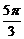

E) 25

$$$39 Е

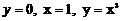 сызық тарымен шектелген облыстың ауданын табың дар

A) 1

B)

C)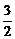

D)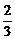

E)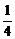

$$$40 D

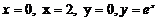 сызық тарымен шектелген облыстың ауданын табың дар

A)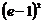

B)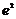

C)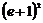

D)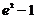

E)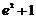

$$$41 C

 сызық тарымен шектелген облыстың ауданын табың дар

A)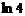

B) 1

C)

D)

E)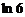

$$$42 E

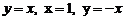 сызық тарымен шектелген облыстың ауданын табың дар

A) 0, 5

B) 3

C) 2

D) 1, 5

E) 1

$$$43 E

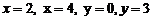 сызық тарымен шектелген фигураның ауданын табың дар

A) 5

B) 2

C) 4

D) 3

E) 6

$$$44 E

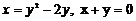 сызық тарымен шектелген фигураның ауданын табың дар

A) 2

B)

C) 1

D)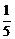

E)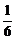

$$$ 45 A

 қ ос интегралын есептең дер, мұ ндағ ы D тө белері 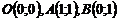 нү ктелерінде жатқ ан ү шбұ рыш

A)

B) 2

C)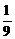

D)

E)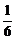

$$$46 В

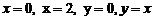 сызық тарымен шектелген фигураның ауданын табың дар

A) 5

B) 2

C) 3

D) 1

E) 4

$$$47 B

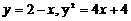 сызық тарымен шектелген фигураның ауданын табың дар

A) 24

B)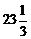

C) 20

D)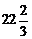

E)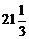

$$$48 D

 сызық тарымен шектелген фигураның ауданын табың дар

A) 3, 2

B) 3, 5

C)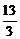

D)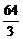

E) 4

$$$49 D

 сызық тарымен шектелген фигураның ауданын табың дар

A) 130

B) 125

C) 128

D) 192

E) 135

$$$50 B

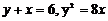 сызық тарымен шектелген фигураның ауданын табың дар

A) 13

B)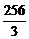

C) 12

D)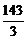

E)

$$$51 E

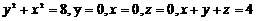 беттерімен шектелген дененің кө лемін табың дар

A)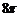

B)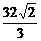

C)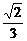

D)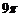

E)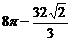

$$$52 В

 беттерімен шектелген дененің кө лемін табың дар

A)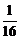

B)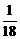

C)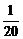

D)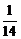

E)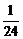

$$$53 А

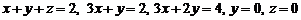 беттерімен шектелген дененің кө лемін табың дар

A)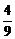

B)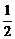

C)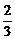

D)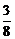

E)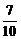

$$$54 В

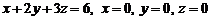 беттерімен шектелген дененің кө лемін табың дар

A) 4

B) 6

C) 8

D) 10

E)12

$$$55 С

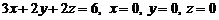 беттерімен шектелген дененің кө лемін табың дар

A) 1

B) 2

C) 3

D) 4

E) 5

$$$56 В

 беттерімен шектелген дененің кө лемін табың дар

A) 1

B) 2

C) 3

D) 4

E) 5

$$$57 Е

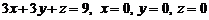 беттерімен шектелген дененің кө лемін табың дар

A)

B)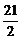

C)

D)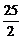

E)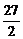

$$$58 В

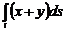 қ исық сызық ты интегралды есептең дер, егер  жә не 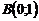 нү ктелерін қ осатын тү зу болса

A) 1

B)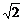

C)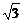

D) 2

E)

$$$59 А

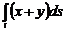 қ исық сызық ты интегралды есептең дер, егер  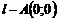жә не  нү ктелерін қ осатын тү зу болса

A)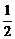

B)

C)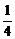

D)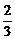

E)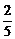

$$$60 С

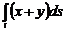 қ исық сызық ты интегралды есептең дер, егер  жә не 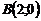 нү ктелерін қ осатын тү зу болса

A)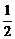

B) 1

C)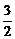

D)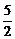

E) 3

$$$61 Е

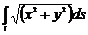 - ті есептең дер, егер  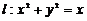шең бері болса

A) 6

B) 5

C) 4

D) 3

E) 2

$$$62 А

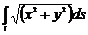 - ті есептең дер, егер  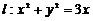шең бері болса

A) 18

B) 19

C) 20

D) 21

E) 22

$$$63 D

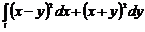 қ исық сызық ты интегралды есептең дер, егер  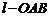сынық сызығ ы болса, мұ ндағ ы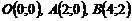

A)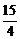

B)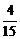

C)

D)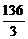

E)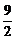

$$$64 С

 қ исық сызық ты интегралды есептең дер, егер 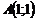 нү ктесінен  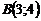нү ктесіне дейінгі жол тү зу сызық тық кесінді болса

A)

B)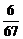

C)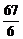

D)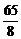

E) 5

$$$65 А

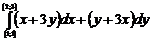 қ исық сызық ты интегралды есептең дер

A)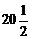

B) 15

C)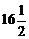

D) 17

E)

$$$66 С

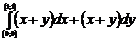 қ исық сызық ты интегралды есептең дер

A) 4

B) 3

C) 2

D) 5

E) 6

$$$67 А

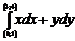 қ исық сызық ты интегралды есептең дер

A) 12

B) 15

C) 13

D) 19

E) 8

$$$ 68А

Еселі интегралды есепте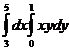

A) 4

B) 6

C) 2

D) 1

E) 0

$$$ 69С

Еселі интегралды есепте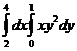

A)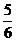

B) 3

C) 2

D) 1

E) 0

$$$ 70А

Еселі интегралды есепте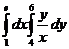

A) 10

B) 8

C)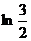

D) 12

E)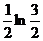

$$$ 71А

Еселі интегралды есепте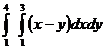

A) 3

B) 2

C) 1

D) 0

E) 0, 5

$$$ 72D

Еселі интегралды есепте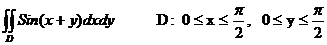

A) 0, 5

B) -1

C) 1

D) 2

E) 0

$$$ 73Е

Еселі интегралды есепте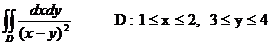

A) 0, 5

B) 0

C)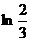

D)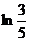

E)

$$$ 74D

Еселі интегралды есепте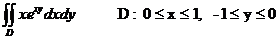

A) е

B) 1

C)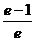

D)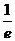

E)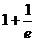

$$$ 75B

Еселі интегралды есепте

A)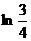

B)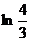

C)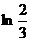

D)

E)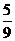

$$$ 76E

Еселі интегралды есепте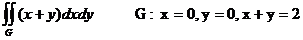

A) 1

B) 0

C) 2

D) 3

E)8/3

$$$ 77А

Еселі интегралды есепте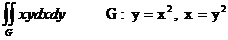

A)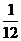

B)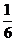

C)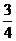

D) 1, 5

E)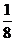

$$$ 78C

Еселі интегралды есепте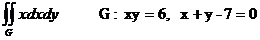

A)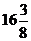

B)

C)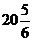

D) 24. 5

E)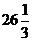

$$$ 79E

Еселі интегралды есепте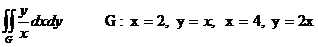

A) 12

B) 4

C) 6

D)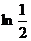

E) 9

$$$ 80E

Еселі интегралды есепте

A) 2

B)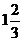

C) 0

D) 1. 4

E)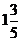

$$$ 81С

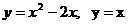 қ исық тарымен шектелген фигураның ауданын тап

A) 4

B)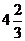

C) 4, 5

D) 6

E) 6, 2

$$$ 82В

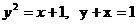 қ исық тарымен шектелген фигураның ауданын тап.

A) 6

B) 4, 5

C) 4

D)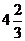

E) 6, 2

$$$ 83А

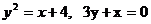 қ исық тарымен шектелген фигураның ауданын тап

A)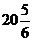

B)

C)

D)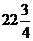

E)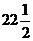

$$$ 84А

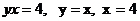 қ исық тарымен қ исық тарымен шектелген фигураның ауданын тап

A) 6-4ln2

B) 6-2ln2

C) 4(1-ln2)

D) 2-ln2

E) жауап кө рсетілгендерден ө згеше

$$$ 85В

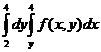 интегралдың интегралдау ретін ө згерт

A)

B)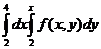

C)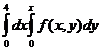

D)

E)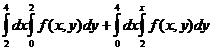

$$$ 86С

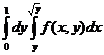 интегралдың интегралдау ретін ө згерт

A)

B)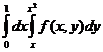

C)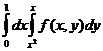

D)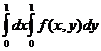

E)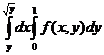

$$$ 87В

Интегралдау тә ртібін ө згерту ережесіне сү йеніп берілген ө рнекті бір екі еселі интеграл арқ ылы жаз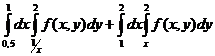

A)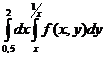

B)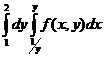

C)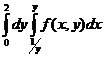

D)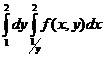

E)

$$$ 88D

Келтірілген формулалардың ішінен дұ рыс емесін кө рсет

A)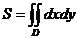

B)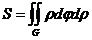

C)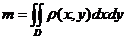

D)

E)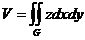

$$$ 89D

2x+3y+4z=12, x=0, y=0, z=0 беттерімен шенелген дененің кө лемін тап.

A) 24

B) 6

C) 16

D) 12

E) 8

$$$ 90Е

Ү ш еселі интегралды есепте

A)

B) 1

C)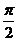

D)

E)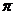

$$$ 91С

Ү ш еселі интегралды есепте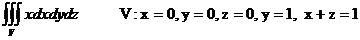

A) 1

B)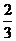

C)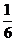

D) 0, 25

E) 1

$$$ 92C

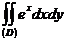 - ті табың дар, мұ ндағ ы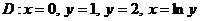

A 1, 5

B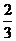

C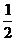

D 2

E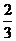

$$$ 93D

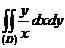 - ті табың дар, мұ ндағ ы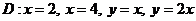


⇐ Предыдущая123456789Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.