Определение реакций при вращении твердого тела вокруг неподвижной оси.

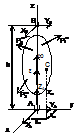
При вращении тела вокруг неподвижной оси возникают динамические давления на опоры. Их определение удобно решать методом кинетостатики. Прикладываем силы инерции для каждой точки: центробежная 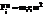, вращательная , r_i– расстояние от точки до оси вращения. Проектируя сумму этих сил на оси и учитывая, что 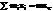и 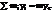, С – центр масс, получаем проекции главного вектора сил инерции:

, .

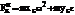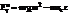Проекции главного момента сил инерции = сумме моментов центробежных и вращательных сил инерций относительно осей координат:

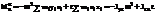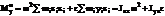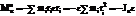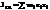, , – центробежные моменты инерции,

Учитывая внешние силы, можно записать уравнения равновесия кинетостатики:

, .

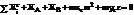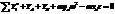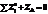
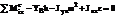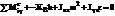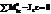Последнее уравнение не содержит реакций опор и представляет собой дифференциальное уравнение вращения тела. Остальные пять уравнений позволяют определить пять неизвестных реакций. Динамические составляющие реакций определяются слагаемыми, которые зависят от сил инерции.

Условия отсутствия динамических составляющих:

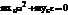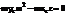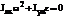, , , , откудаx_C= 0, y_C= 0, J_yz= 0, J_zx= 0, это означает, что центр тяжести должен находиться на оси вращения тела и ось вращения тела z должна быть главной осью инерции тела. Т. е. ось вращения должна являться главной центральной осью инерции тела (ось, которая проходит через центр масс тела, и центробежные моменты инерции с индексом этой оси равны нулю). Для выполнения этого условия проводится специальная балансировка быстро вращающихся тел.

Общие теоремы динамики точки

Теорема об изменении количества движения матер. точки. 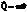– количество движения материальной точки, 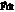– элементарный импульс силы. – элементарное изменение количества движения материальной точки равно элементарному импульсу силы, приложенной к этой точке (теорема в дифференц-ной форме) или 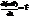– производная по времени от количества движения материальной точки равна равнодействующей сил, приложенных к этой точке. Проинтегрируем: 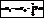– изменение количества движения материальной точки за конечный промежуток времени равно элементарному импульсу силы, приложенной к этой точке, за тот же промежуток времени. – импульс силы за промежуток времени [0, t]. В проекциях на оси координат: и т. д.

Теорема об изменении момента количества движения матер. точки. - момент количества движения матер. точки относительно центра О. 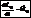– производная по времени от момента количества движения матер. точки относительно какого-либо центра равна моменту силы, приложенной к точке, относительно того же центра. Проектируя векторное равенство на оси координат. получаем три скалярных уравнения: 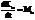и т. д. - производная от момента кол-ва движения матер. точки относительно какой-либо оси равна моменту силы, приложенной к точке, относительно той же оси. При действии центральной силы, проходящей через О, М_О= 0, Þ =const. 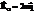=const, где 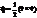– секторная скорость. Под действием центральной силы точка движется по плоской кривой с постоянной секторной скоростью, т. е. радиус-вектор точки описывает (" ометает" ) равные площади в любые равные промежутки времени (закон площадей) Этот закон имеет место при движении планет и спутников – один из законов Кеплера.

Работа силы. Мощность. Элементарная работа dA = F_tds, F_t – проекция силы на касательную к траектории, направленная в сторону перемещения, или dA = Fdscosa.

Если a – острый, то dA> 0, тупой – < 0, a=90^o: dA=0. dA= – скалярное произведение вектора силы на вектор элементарного перемещения точки ее приложения; dA= F_xdx+F_ydy+F_zdz – аналитическое выражение элементарной работы силы. Работа силы на любом конечном перемещении М₀М₁: 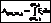. Если сила постоянна, то 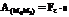= F× s× cosa. Единицы работы: [1 Дж (джоуль) = 1 Нм].

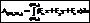, т. к. dx= 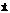dt и т. д., то .

Теорема о работе силы: Работа равнодействующей силы равна алгебраической сумме работ составляющих сил на том же перемещении А=А₁+А₂+…+А_n.

Работа силы тяжести: 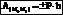, > 0, если начальная точка выше конечной.

Работа силы упругости: –работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины.

Работа силы трения: если сила трения const, то 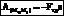- всегда отрицательна, F_тр=fN, f – коэфф. трения, N – нормальная реакция поверхности.

Работа силы тяготения. Сила притяжения (тяготения): 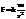, из mg= 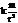, находим коэфф. k=gR². 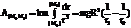– не зависит от траектории.

Мощность – величина, определяющая работу в единицу времени, 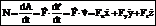. Если изменение работы происходит равномерно, то мощность постоянна: N=A/t. [1 Вт (ватт) =1 Дж/с, 1 кВт (киловатт) =

= 1000 Вт, 1л. с. (лошадиная сила) = 75 кгс× м/с = 736 Вт].

Теорема об изменении кинетической энергии точки. В диффер-ной форме: 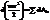– полный дифференциал кинетической энергии мат. точки = элементарной работе всех действующих на точку сил. 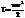– кинетическая энергия матер. точки. В конечном виде: 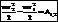– изменение кинетической энергии мат. точки, при переходе ее из начального в конечное (текущее) положение равно сумме работ на этом перемещении всех сил, приложенных к точке.

Силовое поле – область, в каждой точке которой на помещенную в ней матер. точку действует сила, однозначно определенная по величине и направлению в любой момент времени, т. е. должно быть известна 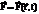. Нестационарное силовое поле, если явно зависит от t, стационарное силовое поле, если сила не зависит от времени. Рассматриваются стационарные силовые поля, когда сила зависит только от положения точки: 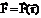и F_x=F_x(x, y, z) и т. д. Свойства стационар. силовых полей:

1) Работа сил стац. поля зависит в общем случае от начального М₁ и конечного М₂ положений и траектории, но не зависит от закона движения матер. точки.

2) Имеет место равенство А_{2, 1}= – А_{1, 2}. Для нестационарных полей эти свойства на выполняются.

Примеры: поле силы тяжести, электростатическое поле, поле силы упругости.

Стационарные силовые поля, работа сил которых не зависит от траектории (пути) движения матер. точки и определяется только ее начальным и конечным положениями назыв. потенциальными (консервативными). , где I и II – любые пути, А_{1, 2} – общее значение работы. В потенциальных силовых полях существует такая функция, однозначно зависящая от координат точек системы, через которую проекции силы на координатные оси в каждой точке поля выражаются так:

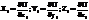. Функция U=U(x₁, y₁, z₁, x₂, y₂, z₂, …x_n, y_n, z_n) назыв. силовой функцией. Элементарная работа сил поля: dА=å dА_i= dU. Если силовое поле является потенц-ным, элементарная работа сил в этом поле равна полному дифференциалу силовой функции. Работа сил на конечном перемещении , т. е. работа сил в потенц-ном поле равна разности значений силовой функции в конечном и начальном положениях и не зависит о формы траектории. На замкнутом перемещении работа равна 0. Потенциальная энергияП равна сумме работ сил потенциального поля на перемещении системы из данного положения в нулевое. В нулевом положении П₀= 0. П=П(x₁, y₁, z₁, x₂, y₂, z₂, …x_n, y_n, z_n). Работа сил поля на перемещении системы из 1-го положения во 2-ое равна разности потенциальных энергий А_{1, 2}= П₁– П₂. Эквипотенциальные поверхности – поверхности равного потенциала. Сила направлена по нормали к эквипотенциальной поверхности. Потенциальная энергия системы отличается от силовой функции, взятой со знаком минус, на постоянную величину U₀: А_{1, 0}= П =U₀ – U. Потенциальная энергия поля силы тяжести: П= mgz. Потенц. энерг. поля центральных сил. Центральная сила – сила, которая в любой точке пространства направлена попрямой, проходящей через некоторую точку (центр), и модуль ее зависит только от расстояния r точки массой m до центра: 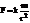, 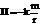. Центральной является гравитационная сила ,

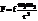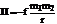, f = 6, 67× 10^-11м³/(кгс²) – постоянная тяготения. Первая космическая скорость v₁= 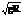» 7, 9 км/с, R = 6, 37× 10⁶м – радиус Земли; тело выходит на круговую орбиту. Вторая космическая скорость: v₁₁= 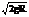» 11, 2 км/с, траектория тела парабола, при v> v₁₁– гипербола. Потенц. энергия восстанавливающей силы пружин:

, l – модуль приращения длины пружины. Работа восстанавливающей силы пружины: 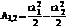, l₁ и l₂ – деформации, соответствующие начальной и конечной точкам пути.

⇐ Предыдущая 1 23