Свойства открытых и замкнутых множеств

Пусть X – метрическое пространство; x0, x, x1, …, xn, … - элементы метр. пр-ва.

Опр. Открытым шаром с центром в точке х0, называется совокупность {x 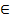Х: 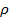(x, х0)< 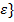, при этом 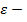это радиус шара. (обозначение: В(х0, )

Опр. Замкнутым шаром с центром в точке x0 радиуса 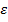называется {x 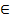Х: 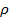(x, х0)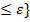

Опр. 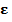– окрестностью называют открытый шар В(х0, (обозначение: U(х0, ))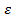

Пусть Х – метрическое пространство; МСХ.

Опр. Точка а называется внутренней точкой для множества М, если существует окрестность точки а U(а), целиком принадлежащая М.

Опр. Точка а называется граничной для множества М, если в любой окрестности U(a) существуют точки как из М, так и не из М.

Опр. Внешней точкой множества М называется такая точка а, для которой существует окрестность U(a), не содержащая точек из М, т. е. U(a) 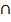М=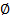

Опр. Совокупность всех граничных точек для множества М называется границей множества М (обозначение: )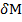

Опр. Дополнением множества М называется множество Х\М (обозначение: СМ)

Свойства:

1) Множества М и СМ имеют общую границу.

2) Для любой граничной точки а множества М cуществует последовательность точек хn 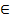М, lim хn=a.

3) Предел любой последовательности { хn}, хn 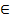М, есть граничная, либо внутренняя точка М.

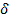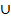4) Пусть даны два множества E и F, тогда (E F) С 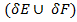(граница объединения двух множеств является подмножеством объединения границ каждого из множеств)

5) Пусть дана совокупность множеств {M 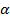}, где {M 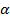}СХ (Х-метр. пространство).

a. Если точка а – внутренняя точка хотя бы одного M 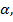то точка а является внутренней точкой множества М= 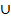M .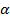

b. Пусть число M 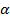– конечное. Тогда если а является внешней для каждого M 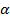, то а является внешней для М.

Х- метр. пр-во, МСХ

Опр. Точка а метрического пространства Х называется предельной точкой множества М, если в любой U(a) содержится хотя бы одна точка из множества М, кроме точки а.

Опр. Точка а из М является изолированной точкой множества М, если существует U(a), не содержащая точек из М, кроме точки а.

Опр. Множество М называется открытым в Х, если:

1) М не содержит ни одной граничной точки;

2) Каждая точка М является внутренней;

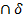3) М М=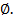

Опр. Множество М метрического пространства Х называется замкнутым, если

1) М содержит все свои граничные точки

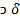2) М М

3) М содержит все свои предельные точки

Свойства открытых и замкнутых множеств

Х-метр. пр-во, МСХ

Т1. Множество М является открытым тогда и только тогда, когда его дополнение СМ – замкнутое.

Т2. В метрическом пространстве объединение любого конечного числа замкнутых множеств есть замкнутое множество