- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Правильные многоугольники.
Треугольники. Замечательные точки:  1. Ортоцентр- пересечение высот (В).
2. Центр тяжести- пересечение медиан (М).
3. Центр вписанной окружности -
пересечение биссектрис (Б).
4. Центр описанной окружности - пере-
сечение серединных перпендикуляров.
1. Ортоцентр- пересечение высот (В).
2. Центр тяжести- пересечение медиан (М).
3. Центр вписанной окружности -
пересечение биссектрис (Б).
4. Центр описанной окружности - пере-
сечение серединных перпендикуляров.
| Средняя линия треугольника проходит через середины двух его сторон параллельно третьей и равна её половине:
Катет, противолежащий углу  равен половине гипотенузы.
У равнобедренных треугольников:
- Углы при основании равны.
- Высота, опущенная на основание, является
биссектрисой и медианой. равен половине гипотенузы.
У равнобедренных треугольников:
- Углы при основании равны.
- Высота, опущенная на основание, является
биссектрисой и медианой.
| Треугольники равны по - 2-м сторонам и углу между ними; - 2-м углам и прилежащей стороне; - 3-м сторонам; - 2-м углам и противолежащей одному из них стороне; - 2-м сторонам и углу, лежащему против большей из них | |||||||||||||||||
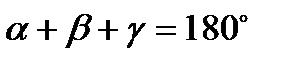 b b
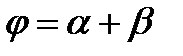
Свойства медиан , биссектри с: - При пересечении медианы делятся в пропорции 2: 1. - Медиана делит площадь треугольника пополам. - Три медианы делят треугольник на 6 равновеликих треугольника.
- Биссектриса . делит противоположные стороны на части, пропорциональные прилежащим к ней сторонам: Средняя линия треугольника: |
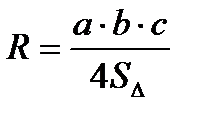 ; ;
Для прямоугольных треугольников:
Для правильных треугольников:
| Треугольники подобны если
- 3 стороны одного пропорциональны 3-м сторонам
другого;
- 2 угла одного равны 2-м углам другого;
- 2 стороны одного пропорциональны 2-м сторонам
другого и углы между ними равны.
Свойства подобных треугольников:
- Площади подобных треугольников пропорциональны
квадратам их сходственных сторон:
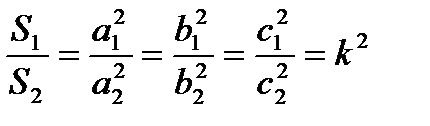 ,
- Периметры подобных треугольников пропорциональны
их сходственным сторонам: ,
- Периметры подобных треугольников пропорциональны
их сходственным сторонам:
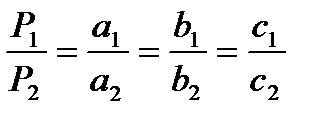 . .
| |||||||||||||||||
| Теорема косинусов:
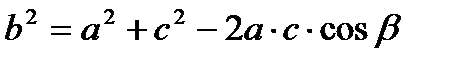
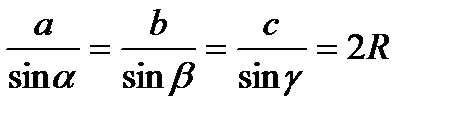
| Площадь треугольника:
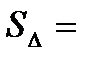 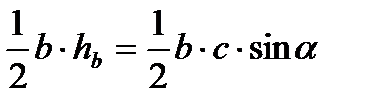 ; ; 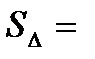 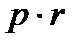 ; ; 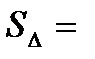 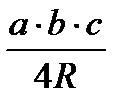 ; ; 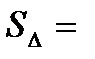 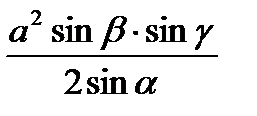 ; ;
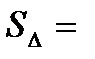 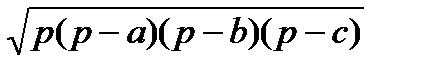 -формула Герона -формула Герона
| - Высота прямоугольного треугольника, проведенная из вершины прямого угла, делит его на два подобных, каждый из которых подобен данному. | |||||||||||||||||
Прямоугольные треугольники:
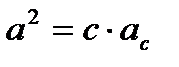
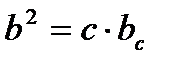

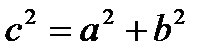 - теорема Пифагора - теорема Пифагора
a |
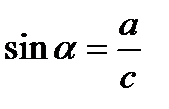 ; ; 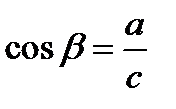 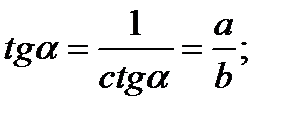
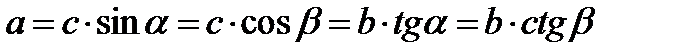 ; ;
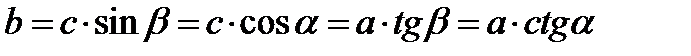 . .
| Дополнительная информация: - Медиана, проведенная из вершины прямого угла равна половине гипотенузы. - Если медиана, высота и биссектриса, проведенные к разным сторонам, пересекаются в одной точке, то треугольник равносторонний. |
Четырехугольники.
1. Длялюбогочетырехугольника 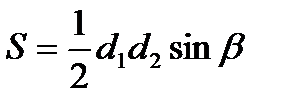 ,
где ,
где 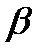 - острый угол между диагоналями.
2. В любой четырехугольник можно вписать окружность, если суммы противоположных сторон равны.
3. Около любого четырехугольника можно описать окружность, еслисуммыпротивоположных углов в нем равны - острый угол между диагоналями.
2. В любой четырехугольник можно вписать окружность, если суммы противоположных сторон равны.
3. Около любого четырехугольника можно описать окружность, еслисуммыпротивоположных углов в нем равны 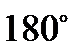 .
4. Диагонали четырехугольника перпендикулярны, если сумма квадратов противоположных сторон равна сумме квадратов двух других сторон. .
4. Диагонали четырехугольника перпендикулярны, если сумма квадратов противоположных сторон равна сумме квадратов двух других сторон.
| Окружности и углы.
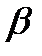 - вписанный угол; - вписанный угол;
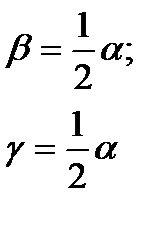
Вписанный угол, опирающийся
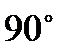
|
Правильные многоугольники.
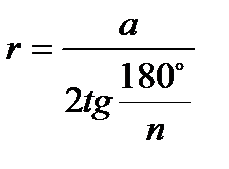 ; ;
| |||||||||||
Параллелограмм:
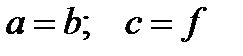 . .
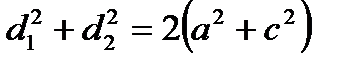 . .
5. |
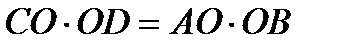
| 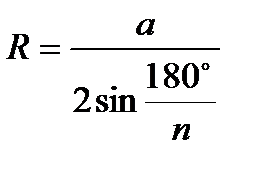 ; ;
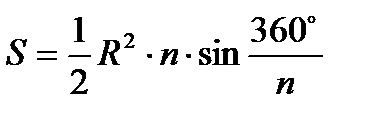
| |||||||||||
| Ромб: 1.
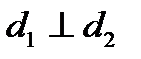 . .
4. 4. |
проведенные из одной точки к окружности равны.
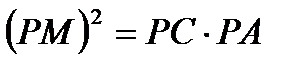 , ,
где РС - секущая. | Правильный треугольник:
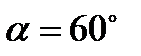 ; ; 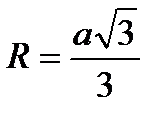 ; ; 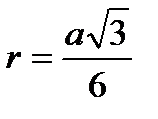 ;
Сумма углов = ;
Сумма углов = 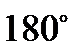 .
Правильный четырехугольник: .
Правильный четырехугольник:
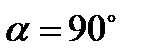 ; ; 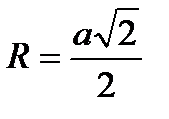 ; ; 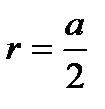 ; ;
| |||||||||||
Трапеция:
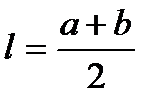 - средняя линия - средняя линия
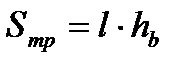 . .
В равнобочной трапеции: - если
| 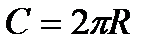 - длина окружности; - длина окружности;
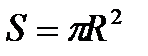 - площадь круга; - площадь круга;
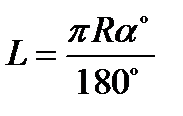 - длина дуги; - длина дуги;
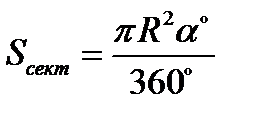 - площадь кругового сектора; - площадь кругового сектора;
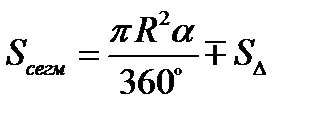 - площадь сегмента - площадь сегмента
| Сумма углов = 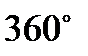 .
Правильный шестиугольник: .
Правильный шестиугольник:
 ; ; 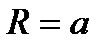 ; ; 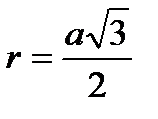 ;
Сумма углов = ;
Сумма углов = 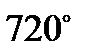 . .
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
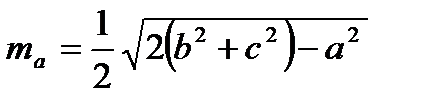 .
. 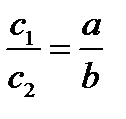 ,
, 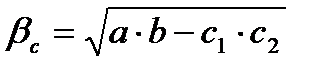 .
. 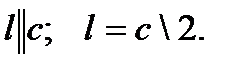
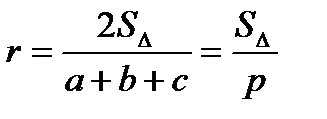 ;
; 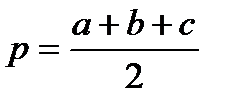 ;
; 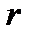 - радиус вписанной окружности;
- радиус вписанной окружности; 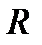 - радиус описанной окружности.
- радиус описанной окружности. 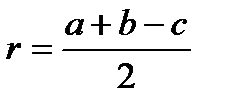 ;
; 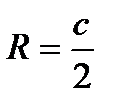 ;
; 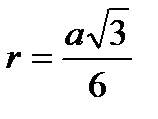 ;
; 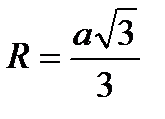 ;
; 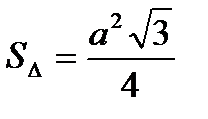 .
. 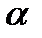 - центральный угол;
- центральный угол; 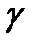 - угол между хордой и касательной
- угол между хордой и касательной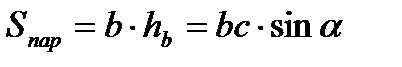 .
. 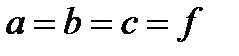 .
.  .
. 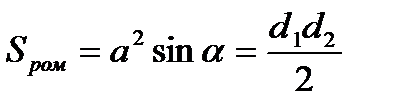
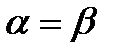 ;
;  .
. 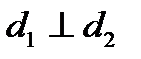 , то
, то