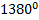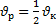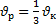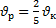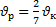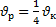- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
РТ2015-2016 гг. Этап I.Вариант 2
РТ2015-2016 гг. Этап I. Вариант 2
| А7 | Вычислите |
1)  2) -
2) -  3) 3
4) 1
5) 27
3) 3
4) 1
5) 27
| ||
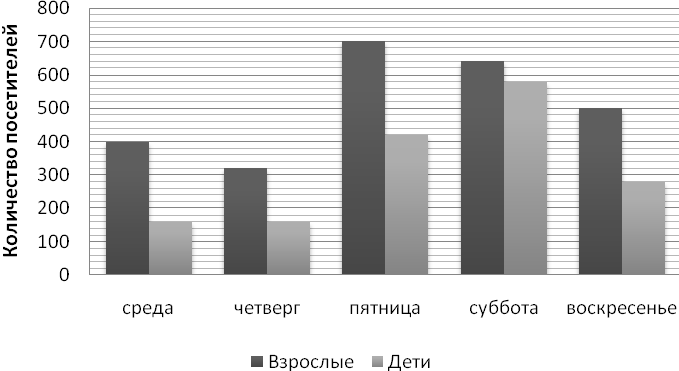
| А8 | На диаграмме показано количество посетителей музея (взрослые и дети) со среды по воскресенье. В какой день среди посетителей музея детей было на 40 % меньше, чем взрослых?
| 1) среда 2) четверг 3) пятница 4) суббота 5) воскресенье | ||
| А9 |
| 1) -3 2) -4 3) 6 4) -5 5) 0 | ||
| А10 | Сократите дробь |
1) 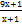 2) 2) 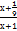 3)9-8х 4)
3)9-8х 4) 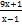 5)
5) 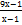
| ||
| А11 |
|
1) – 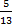 2) 2) 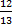 3) -
3) - 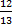 4) 4) 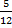 5)
5) 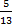
| ||
| А12 | Найдите значение выражения 8sin | 1)1 2)-6+2 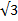 3)2
3)2 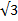 4)4 4)4 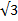 5) -1
5) -1
| ||
|
А13 | Расстояние от пунктаАдо пункта В по реке плот проходит за 14 часов, а катер – за 4 часа. Скорость течения реки 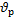 и собственная скорость катера и собственная скорость катера 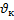 связаны формулой: связаны формулой:
| 1) 2) 3) 4) 5) | ||
|
А14 | Для группы туристов был закуплен сухой паёк, в который вошли 238 банок тушёнки, 170 плиток шоколада и 204 пакетика чая. Определите наибольшее возможное количество туристов в группе, если все продукты были распределены между ними поровну. | 1) 170 2) 85 3) 68 4) 34 5) 17
| ||
|
А15 | Сумма корней уравнения 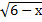 ( ( 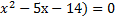 равна: равна:
| 1) 4 2) -1 3) 11 4) 13 5) 5 | ||
|
А16 | 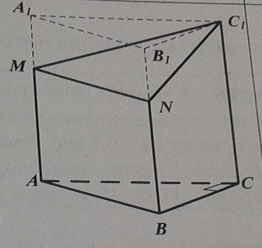 От прямой треугольной призмы От прямой треугольной призмы  , основанием которой является прямоугольный равнобедренный треугольник АВС (уголС= , основанием которой является прямоугольный равнобедренный треугольник АВС (уголС=  ), плоскостью отсекли меньшую часть объёмом 18 так, как показано на рисунке (MN ), плоскостью отсекли меньшую часть объёмом 18 так, как показано на рисунке (MN 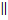 AB, AB, 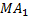 = = 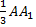 ). Найдите объём призмы ). Найдите объём призмы 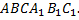
| 1) 27 2) 81 3) 42 4) 36 5) 24 | ||
|
А17 | Если функция, заданная формулой y=kx+b, является нечётной и точкаА(4; 3) принадлежит её графику, то значение выражения k+b равно: | 1) 7 2) 4 3) 3
4)
5) | ||
|
А18 | Вычислите ( 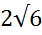 - 1) ( - 1) ( 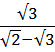 - - 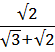 ). ).
| 1) -23 2) 1 3) -25 + 4 4) 2 5) 4 | ||
Часть В
Ответы, полученные при выполнении заданий части В, запишите в бланке ответов. Каждую цифру и знак минус (если число отрицательное) пишите в отдельной клеточке (начиная с первой) по образцам, указанным в бланке. Ответом должно быть некоторое целое число.
| В1 | Автомобиль проехал 60 километров по городу и 190 километров по трассе, израсходовав при этом 26, 2 литров топлива. Известно, что автомобилю на каждые 100 километров пробега по городу требуется на 2 литра топлива больше, чем на каждые 100 километров пробега по трассе. Сколько литров топлива автомобиль израсходовал на трассе? |
| В2 | Пусть (х; у) – решение системы уравнений 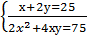 . Найдите значение выражения 2у-х. . Найдите значение выражения 2у-х.
|
| В3 | Из точки к плоскости проведены перпендикуляр и наклонная, длина которой равна 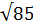 . Найдите длину проекции наклонной на эту плоскость, если она длиннее перпендикуляра на 1. . Найдите длину проекции наклонной на эту плоскость, если она длиннее перпендикуляра на 1.
|
| В4 | Найдите наибольшее значение функции у= 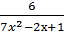
|
| В5 | АВСD – трапеция, у которой AD 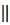 BC BC 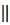 OX, угол BAD= OX, угол BAD= 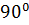 , A(3; 4), C (6; 8), BD = , A(3; 4), C (6; 8), BD = 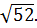 Найдите сумму координат точки D. Найдите сумму координат точки D.
|
| В6 | Количество целых решений неравенства 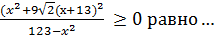
|
| В7 | Из пунктов А и В, находящихся друг от дурга на расстоянии 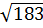 м, равномерно и прямолинейно движутся в пунктС два тела. Скорость первого тела равна 1 м/с, второго – 0, 5 м/с. Какое суммарное расстояние ( в метрах) прошли оба тела до пунктаС, если известно, что первое прибыло в пункт С на 12 секунд позже второго и угол АВС равен м, равномерно и прямолинейно движутся в пунктС два тела. Скорость первого тела равна 1 м/с, второго – 0, 5 м/с. Какое суммарное расстояние ( в метрах) прошли оба тела до пунктаС, если известно, что первое прибыло в пункт С на 12 секунд позже второго и угол АВС равен 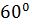 ? ?
|
| В8 | Решите уравнение 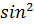 x + x + 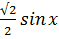 = 0. В ответ запишите его корень (в градусах), принадлежащий промежутку = 0. В ответ запишите его корень (в градусах), принадлежащий промежутку 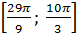 . .
|
| В9 | Окружность радиуса 6, вписанная в ромб, делит одну из его диагоналей на отрезки, длины которых относятся как 1: 6: 1. Найдите площадь ромба S, в ответ запишите значение выражения 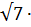 S. S.
|
| В10 | Найдите сумму целых решений неравенства 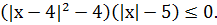
|
| В11 | Через середины двух смежных рёбер основания правильной четырёхугольной призмы проведена плоскость так, что она пересекает три боковых ребра и составляет с плоскостью основания угол 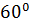 . Длина ребра основания призмы равна 6. Определите площадь полученного сечения. . Длина ребра основания призмы равна 6. Определите площадь полученного сечения.
|
| В12 | Петя выписал целые числа от 100 до 900, которые при делении на 4 и на 6 дают в остатке 1, а при делении на 9 дают в остатке 7. Сколько таких чисел получилось у Пети? |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
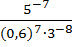
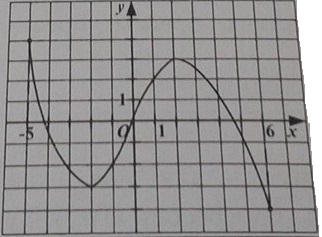 Функция у(х) задана графиком на промежутке [-5; 6]. Наименьшее значение функции равно:
Функция у(х) задана графиком на промежутке [-5; 6]. Наименьшее значение функции равно: 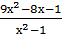
 На координатной плоскости изображён тупоугольный треугольник ABC с вершинами вузлах сетки(см. рисунок). Синус угла ABC этого треугольника равен:
На координатной плоскости изображён тупоугольный треугольник ABC с вершинами вузлах сетки(см. рисунок). Синус угла ABC этого треугольника равен: 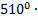 cos(-
cos(- 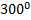 )
)  tg
tg 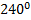 -4 sin
-4 sin