
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Основні засоби розв'язку тригонометричних рівнянь
Основні засоби розв'язку тригонометричних рівнянь
Повторення: Для розв'язання найпростіших тригонометричних рівнянь використовуються формули їх загальних рішень та окремі випадки, подані у наступній таблиці:
| Уравнение | Общее решение | Частные случаи | Приложения |
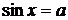
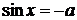
| 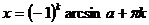
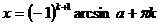
| 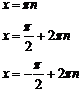 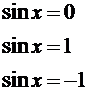  
|
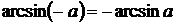 | a |
| a | 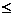 1. 1.
|
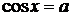
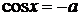
| 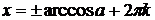
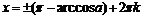
| 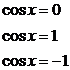 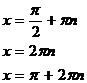
|
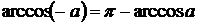 | a |
| a | 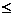 1. 1.
|
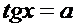 tgх = - a
tgх = - a
|
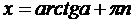 x = - arctg a +pn
x = - arctg a +pn
|
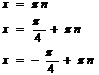 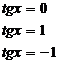
|
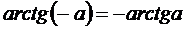 a Î R.
a Î R.
|
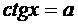 ctg х= - a
ctg х= - a
|
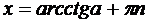 x = p - arcctg a +pn
x = p - arcctg a +pn
| 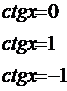 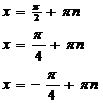
|
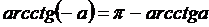 a Î R.
a Î R.
|
Решение уравнений, сводящихся к простейшим
а)  б)
б) 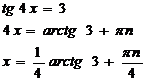
в) cos x = p/4 –решений нет, т. к cos x не может быть равен углу
Решение дробно-рациональных уравнений:
а) 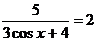 - решаем, используя свойство пропорции
- решаем, используя свойство пропорции
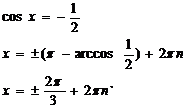 Данное уравнение имеет решения при условии: 3cos x + 4
Данное уравнение имеет решения при условии: 3cos x + 4 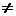 0; cos x
0; cos x 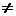 -4/3, следовательно не существует такого значения х, при котором знаменатель дроби обращается в 0.
-4/3, следовательно не существует такого значения х, при котором знаменатель дроби обращается в 0.
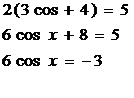
Ответ: 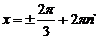 nÎ Z
nÎ Z
б) 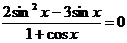 Дробь равнa 0, если её числитель равен 0, а знаменатель отличен от 0: Далее уравнение решается в виде системы
Дробь равнa 0, если её числитель равен 0, а знаменатель отличен от 0: Далее уравнение решается в виде системы
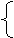 2 sin2 x – 3 sin x = 0
2 sin2 x – 3 sin x = 0
1 + cos x 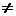 0
0
решаем первое уравнение системы: 2 sin2x – 3sinx = 0; sinx(2 sinx - 3) = 0,
откуда sinx = 0 или 2 sinx – 3 = 0
1) sinx = 0, х = pn, nÎ Z;
1) 2 sinx – 3 = 0; sinx = 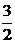 - решений нет
- решений нет
Второе условие: 1 + cos x 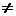 0 выполняется, если cos x
0 выполняется, если cos x 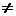 -1, т. е. x
-1, т. е. x 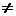 p + 2pk, kÎ Z
p + 2pk, kÎ Z
 Таким образом, данная система равносильна системе: у
Таким образом, данная система равносильна системе: у
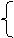 х = pn, nÎ Z;
х = pn, nÎ Z;
 x
x 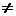 p +2pk, kÎ Z
p +2pk, kÎ Z
 На единичной окружности отмечаем числа:
На единичной окружности отмечаем числа:



 х = pn, nÎ Z и выбираем те, которые удовлетворяют p 0 0 2p х
х = pn, nÎ Z и выбираем те, которые удовлетворяют p 0 0 2p х
условию x 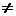 p + 2pk, kÎ Z.
p + 2pk, kÎ Z.
Это будут числа: х = 2pn, nÎ Z (четные значения 2pn, 4pn…)
Ответ: х = 2pn, nÎ Z
Решение тригонометрических уравнений методом разложения на множители:
а) 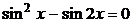 ;
; 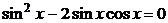 ;
; 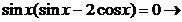
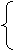
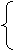
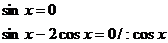

Найдем решения второго уравнения:
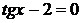 ;
; 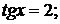
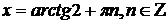
Ответ: 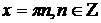 ,
, 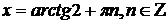
б) cos (p/4 + x) – tg 3x · cos (p/4 + x) = 0; выносим за скобки общий множитель
cos (p/4 + x), получаем cos (p/4 + x)(1 - tg 3x) = 0, решаем далее системой
 cos (p/4 + x) = 0 (частный случай)
cos (p/4 + x) = 0 (частный случай)
1 - tg 3x = 0
 p/4 + x = p/2 + pn
p/4 + x = p/2 + pn
tg 3x = 1 (частный случай)
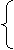
x = p/2 - p/4 + pn
3x = p/4 + pn
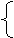 x = p/4 + pn
x = p/4 + pn
x = p/12 + pn/3 Ответ: { p/4 + pn; p/12 + pn/3, nÎ Z}
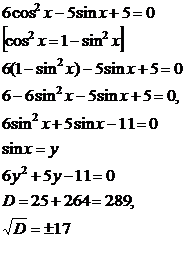 Решение тригонометрических уравнений алгебраическим методом (сведения к одной тригонометрической функции):
Решение тригонометрических уравнений алгебраическим методом (сведения к одной тригонометрической функции):
 - переход к одной тригонометрической функции
- переход к одной тригонометрической функции
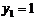
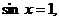
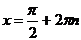
 не является решением
не является решением
Ответ: 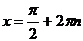 nÎ Z
nÎ Z
Решение однородных уравнений:
О: Уравнение вида
(1) 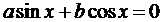 - называется однородным тригонометрическим уравнением 1 степени (линейным)
- называется однородным тригонометрическим уравнением 1 степени (линейным)
(2) 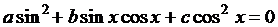 - называется однородным тригонометрическим уравнением II степени.
- называется однородным тригонометрическим уравнением II степени.
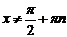 Рассмотрим уравнение (1)
Рассмотрим уравнение (1) 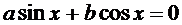 , где а, b
, где а, b 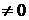 ,
,
пусть cos x 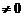 , т. е
, т. е
Делим обе части уравнения на cos x, получаем уравнение вида:
а tgх + b=0, откуда 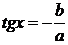 ;
; 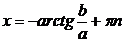 - решение
- решение
Итак, однородное тригонометрическое уравнение 1й степени 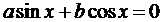 имеет общее решение
имеет общее решение 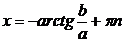 nÎ Z
nÎ Z
Пример:
sinx + 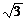 cosx = 0; x = - arcctg
cosx = 0; x = - arcctg 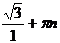 ; x = - arcctg
; x = - arcctg 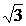 +pn; x = -
+pn; x = - 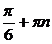 - ответ
- ответ
Рассмотрим уравнение (2) 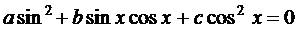
пусть 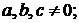
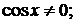
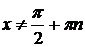 ;
;
Делим обе части уравнения на cos2x и получаем уравнение вида: 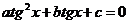 ,
,
производим замену переменной: 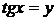 и получаем квадратное уравнение относительно у:
и получаем квадратное уравнение относительно у:
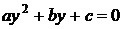 , решив которое, находим значение для tgx, а затем и значение самого х.
, решив которое, находим значение для tgx, а затем и значение самого х.
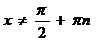 Пример:
Пример:
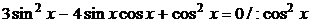 , где
, где
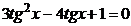 ;
;
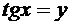 - замена;
- замена;
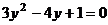
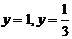
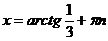
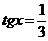
Следовательно,
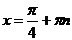
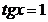
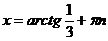
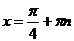 Ответ:
Ответ:
nÎ Z
Решение систем тригонометрических уравнений.
Основные методы решения систем тригонометрических уравнений почти такие же, как и методы решения алгебраических систем (сложение и подстановка).
 а) sin x – cos y = 1 (1)
а) sin x – cos y = 1 (1)
sin x + cos y = 0 (2) складывая и вычитая почленно уравнения (1) и (2), получаем
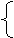 2 sin x = 1 sin x =1/2 x =(-1)k p/6 + pk, kÎ Z
2 sin x = 1 sin x =1/2 x =(-1)k p/6 + pk, kÎ Z
2 cos y = -1 cos y = -1/2 x = 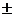 2p/3 + 2pn, nÎ Z
2p/3 + 2pn, nÎ Z
Ответ: x =(-1)k p/6 + pk, kÎ Z
x = 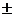 2p/3 + 2pn, nÎ Z
2p/3 + 2pn, nÎ Z
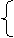 б) x + y = p
б) x + y = p
cos x – cos y = 1 Из первого уравнения находим у = p - х, подставляем во второе уравнение и получаем cos x – cos (p - х) = 1; cos x + cos x =1; 2 cos x = 1; cos x = ½;
x = 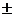 p/3 + 2pn, nÎ Z
p/3 + 2pn, nÎ Z
Тогда у = p - ( 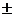 p/3 + 2pn) =
p/3 + 2pn) = 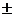 p/3 + (1 – 2n)p, nÎ Z
p/3 + (1 – 2n)p, nÎ Z
Ответ: x = 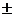 p/3 + 2pn, у =
p/3 + 2pn, у = 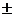 p/3 + (1 – 2n)p, nÎ Z.
p/3 + (1 – 2n)p, nÎ Z.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|