
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Сечение х=2м.
Министерство образования и науки Украины
Национальная академия природоохранного и курортного строительства
Архитектурно-строительный факультет
Кафедра: МиСС
Расчётно-графическая работа № 1
«Исследование напряженного состояния полосы-балки»
Вариант № 5
Выполнил:
студент группы ПГС-301
Булгару М. А.
Проверил:
Профессор
Чемодуров В. Т.
Симферополь, 2014 год
Рассматривается полоса-балка узкого прямоугольного профиля длиной L=4м, высотой h=2 м и толщиной b=1. Объемными силами пренебрегаем. Задано выражение для функций напряжений:
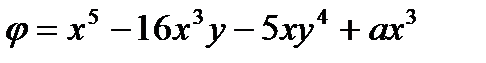 , где а=5
, где а=5
Требуется:
А) проверить, может ли данная функция быть принята для решения плоской задачи теории упругости,
Б) пользуясь соотношениями Эри, найти выражения для напряжений,
В) построить эпюры напряжений для одного сечения, перпендикулярного оси Х (х=2м), и второго - перпендикулярного оси У (у=0, 5м),
Г) установить граничные воздействия (нормальные и касательные) на полосу, дать их изображение на рисунке полосы-балки и привести соответствующие эпюры.
Решение:
А) Проверим, удовлетворяет ли заданная функция бигармоническому уравнению:
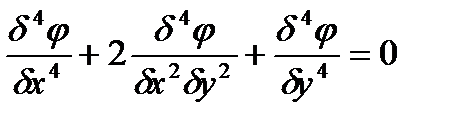
Для этого найдем соответствующие производные:
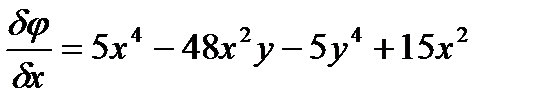
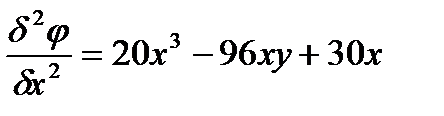
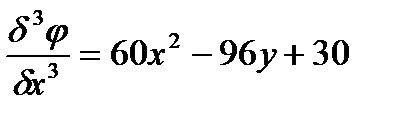
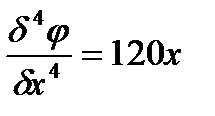
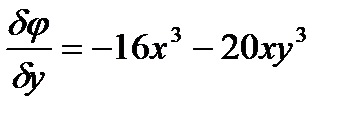
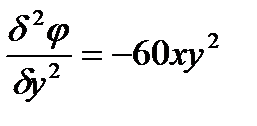
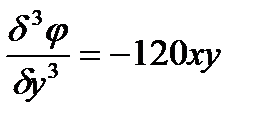
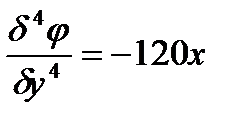
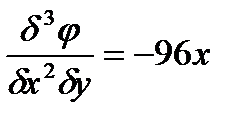
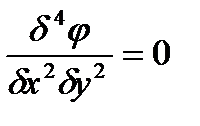
Подставим найденные значения производных в уравнение:
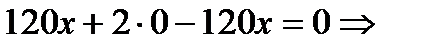
Заданное выражение для функций напряжений удовлетворяет исходному уравнению и может быть принято для решения плоской задачи теории упругости.
Б) Находим выражения для напряжений, пользуясь соотношением Эри:
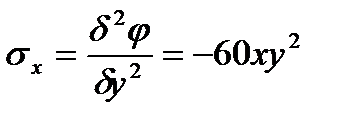
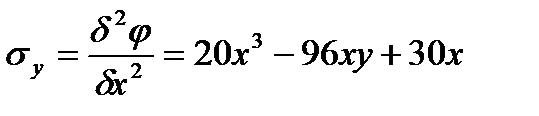
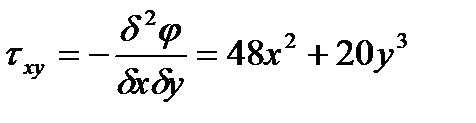
В) Строим эпюры напряжений, действующих в сечениях х=2м и у=0, 5м. Эпюры строим по характерным точкам, которыми являются граничные, экстремальные и точки перегиба.
Сечение х=2м.
В этом сечении действуют:
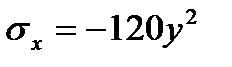
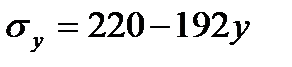

Получены три функции ординаты у ( 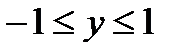 ). Для характерных точек находим:
). Для характерных точек находим:
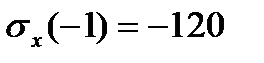
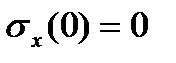

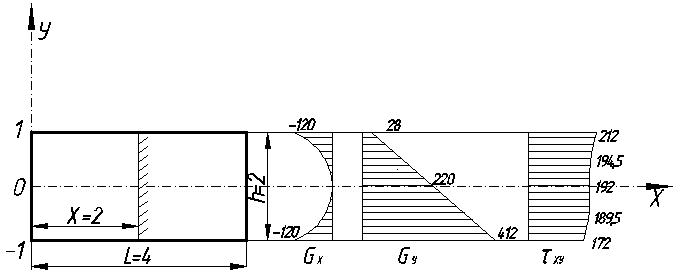
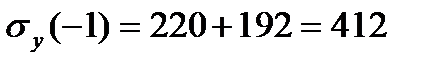
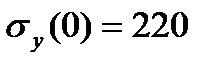
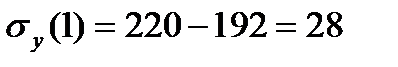
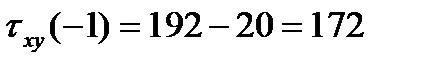

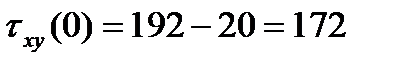
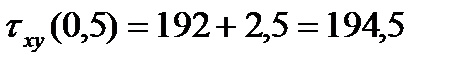
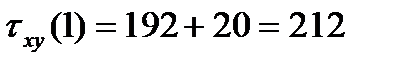
По полученным значениям строим эпюры: 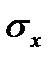 ,
, 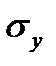 ,
, 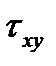
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|