Пример решения задачи.. тыс. руб.

Пример решения задачи.

ЗАДАЧА.

Имеются данные о товарообороте магазина по месяцам за 1994 год:

Месяцы	Товарооборот, тыс. руб.
январь
февраль
март
апрель
май
июнь
июль

1. Рассчитать аналитические (цепные и базисные) и средние показатели динамического ряда.

2. Выровнять ряд:

· А) методом скользящей средней;

· Б) методом аналитического выравнивания ( линейный тренд способом отсчета от условного нуля).

3. Изобразить на графике фактический ряд и ряды выравненных значений.

РЕШЕНИЕ.

1. По имеющимся формулам рассчитываем сначала аналитические показатели динамики (цепные и базисные) и оформляем решение в виде таблицы:

Таблица 10. 1

Месяц	Товарообороттыс. руб. (у)	Δ y, тыс. руб.		Кр		Тр, %		Тпр, %		Абсол. значение 1% прироста
Месяц	Товарообороттыс. руб. (у)	цеп.	баз.	цеп.	баз.	цеп.	баз.	цеп.	баз.	цеп.	баз.
Январь		х	х	х	х	х	х	х	х	х	х
Февраль		-20	-20	0, 933	0, 933	93, 3	93, 3	-6, 7	-6, 7	3, 0	3, 0
Март				1, 161	1, 083	116, 1	108, 3	16, 1	8, 3	2, 8	3, 0
Апрель		-5		0, 985	1, 067	98, 5	106, 7	-1, 5	6, 7	3, 25	3, 0
Май				1, 125	1, 200	112, 5	120, 0	12, 5	20, 0	3, 2	3, 0
Июнь				1, 056	1, 267	105, 6	126, 7	5, 6	26, 7	3, 6	3, 0
Июль		-10		0, 974	1, 233	97, 4	123, 3	-2, 6	23, 3	3, 8	3, 0
Итого			х	х	х	х	х	х	х	х	х

После проведения расчетов проверим взаимосвязь между цепными и базисными абсолютными приростами: сумма всех цепных приростов за период должна давать общий прирост за весь рассматриваемый период. В нашем случае это равенство выполнено:

Σ Δ у^ц= 70 =Δ y_t^б

Проверяем взаимосвязь между цепными и базисными коэффициентами роста: произведение всех цепных коэффициентов роста за период должно давать базисный коэффициент роста за весь рассматриваемый период. В нашем случае:

Кр₁^ц· Кр₂^ц· Кр₃^ц· Кр₄^ц· Кр₅^ц· Кр₆^ц = 0, 933 · 1, 161 · 0, 985 · 1, 125 · 1, 056 · 0, 974 = 1, 233 = Кр₆^б.

Затем подсчитываем средние показатели динамики:

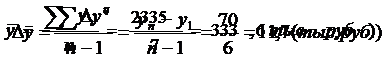А) Средний уровень ряда ( считается по формуле средней арифметической, так как мы имеем интервальный ряд динамики):

Б) Средний абсолютный прирост:

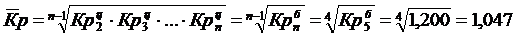В) Средний коэффициент роста (считается по формуле средней геометрической). В целях облегчения вычисления рассчитаем этот показатель для пяти месяцев (в связи с простотой вычисления корня четвертой степени):

Г) Средний темп роста:

Д) Средний темп прироста:

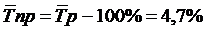2. Проводим выравнивание ряда.

А) Метод скользящей средней.

Возьмем в качестве укрупненного интервала период в три месяца. Тогда первая скользящая средняя будет равна товарообороту первых трех месяцев, деленному на количество этих месяцев: (300+280+325): 3 = 301, 67 тыс. руб. Эта средняя будет относиться к середине укрупненного интервала, то есть к февралю. Проведем аналогичные расчеты для февраля, марта и апреля и т. д. Результаты оформим в виде таблицы:

Таблица 10. 2

Месяцы	Товарооборот, тыс. руб.	Скользящие средние, тыс. руб.
Январь		-
Февраль		(300+280+325): 3=301, 67
Март		(280+325+320): 3=308, 33
Апрель		(325+320+360): 3=335
Май		(320+360+380): 3=353, 33
Июнь		(360+380+370): 3=370
Июль		-

Б) Аналитическое выравнивание

Отметим, что в современных условиях можно значительно упростить расчеты аналитического уравнения тренда и выравненных значений показателя при помощи электронных таблиц EXCEL, в которых предусмотрены соответствующие статистические функции. Так, выравнивание по линейному тренду осуществляется с использованием функций ПРЕДСКАЗ или ТЕДЕНЦИЯ, а по экспоненте – функции РОСТ.

3. Изобразим на графике ряды фактических и выравненных значений.

Для характеристики динамики при достаточно большом числе наблюдений чаще всего применяются линейные диаграммы. Они строятся в прямоугольной системе координат. По оси абсцисс откладываем отрезки, соответствующие периодам времени (в нашем случае месяцы), а по оси ординат – уровни ряда динамики. Полученные точки соединяем отрезками в виде ломаной линии.

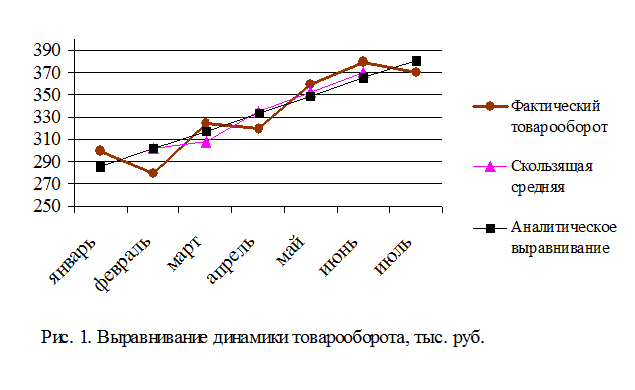
Изобразим на одном графике три ряда: фактические значения товарооборота, результаты выравнивания по методу скользящей средней и аналитического выравнивания по прямой. Поскольку нас интересуют в данном случае не абсолютные, а относительные изменения, то для удобства можно установить в качестве минимального значения по оси ординат не нулевое значение, а, например, 250 тыс. руб.