
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Приложение 1. Варианты заданий. для индивидуальной самостоятельной работы. Вариант 1. Вариант 2. Вариант 3
Приложение 1
Варианты заданий
для индивидуальной самостоятельной работы
Вариант 1
1. Вычислить:
1) 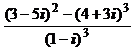 ; 2)
; 2) 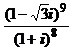 ; 3)
; 3) 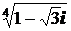 .
.
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) | z - i |> 1; 2) | z - i +3|£ 3.
3. Разделить многочлен f ( x )=3 x 4-5 x 3+4 x 2-2 x +1 на многочлен g ( x )=3 x 3-2 x 2+ x -1 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
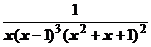 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
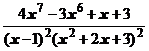 .
.
Вариант 2
1. Вычислить:
1) 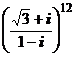 ; 2)
; 2) 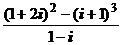 ; 3)
; 3) 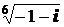 .
.
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) | z -2+3 i |£ 3; 2) | z + i |> 4.
3. Разделить многочлен f ( x )= x 5+5 x 4+9 x 3+7 x 2+5 x +3 на многочлен g ( x )= x 4+2 x 3+2 x 2+ x +1 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
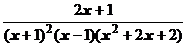 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
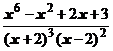 .
.
Вариант 3
1. Вычислить:
1) 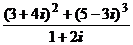 ; 2)
; 2) 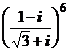 ; 3)
; 3) 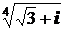 .
.
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) | z -2+ i |£ 2; 2)| z + i |=2.
3. Разделить многочлен f ( x )= x 4+1 на многочлен g ( x )= x 3+ x с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
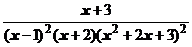 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
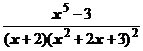 .
.
Вариант 4
1. Вычислить:
1) 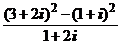 ; 2)
; 2) 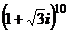 ; 3)
; 3) 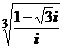 .
.
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+2i|> 3; 2) |z-1-2i|£ 1.
3. Разделить многочлен f(x)=x4-x2+x-1 на многочлен g(x)=x3-1 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
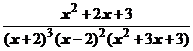 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
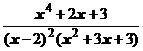 .
.
Вариант 5
1. Вычислить:
1) 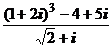 ; 2)
; 2) 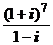 ; 3)
; 3) 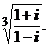
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+2i-3|> 2; 2) |z-3i|£ 3.
3. Разделить многочлен f(x)=x4-x3-x2-1 на многочлен g(x)=x3+1 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
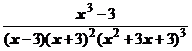 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
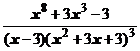 .
.
Вариант 6
1. Вычислить:
1) 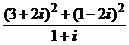 ; 2)
; 2) 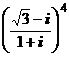 ; 3)
; 3) 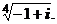
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z-2i-3|> 2; 2) |z+3i|£ 1.
3. Разделить многочлен f(x)=x6-4x5+11x4-27x3+37x2-35x+35 на многочлен g(x)=x5-3x4+7x3-20x2+10x-25 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
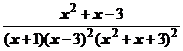 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
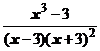 .
.
Вариант 7
1. Вычислить:
1) 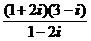 ; 2)
; 2) 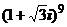 ; 3)
; 3) 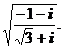
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+1+2i|³ 1; 2) |z-3i|< 3.
3. Разделить многочлен f(x)=3x7+6x6-3x5+4x4+14x3-6x2-4x+4 на многочлен g(x)=3x6-3x4+7x3-6x+2 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
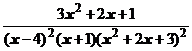 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
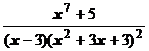 .
.
Вариант 8
1. Вычислить:
1) 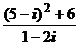 ; 2)
; 2) 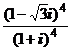 ; 3)
; 3) 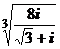 .
.
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+2i|£ 1; 2) |z+1+i|> 3.
3. Разделить многочлен f(x)=3x3-2x2+x+2 на многочлен g(x)=x2-x+1 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
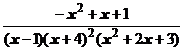 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
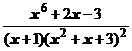 .
.
Вариант 9
1. Вычислить:
1) 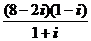 ; 2)
; 2) 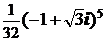 ; 3)
; 3) 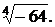
2. Описать геометрическое множество чисел, удовлетворяющих неравенствам:
1) |z+4+2i|> 1; 2) |z-5i|£ 3.
3. Разделить многочлен f(x)=x4-x3-4x2+4x+1 на многочлен g(x)=x2-x-1 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
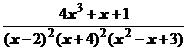 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
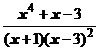 .
.
Вариант 10
1. Вычислить:
1) 
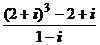 ; 2)
; 2) 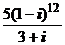 ; 3)
; 3) 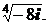
2. Описать множество комплексных чисел, удовлетворяющих неравенствам
1) |z-1+3i|£ 2 2) |z+2i|> 2.
3. Разделить многочлен f(x)=3x5+5x4-16x3-6x2-5x-6 на многочлен g(x)=3x4-4x3-x2-x-2 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
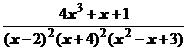 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
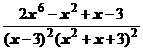 .
.
Вариант 11
1. Вычислить:
1) 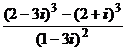 ; 2)
; 2) 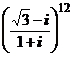 ; 3)
; 3) 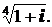
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z-i+2|£ 1; 2) |z-4i|> |.
3. Разделить многочлен f(x)=x5-5x4-2x3+12x2-2x+12 на многочлен g(x)=x3-5x2-3x+17 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
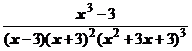 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
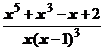 .
.
Вариант 12
1. Вычислить:
1) 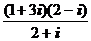 ; 2)
; 2) 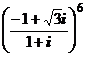 ; 3)
; 3) 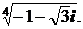
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+i+2|£ 1; 2) |z+3i|> 3.
3. Разделить многочлен f(x)=x5-5x4-2x3+12x2-2x+12 на многочлен g(x)=x3-5x2-3x+17 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
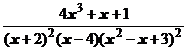 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
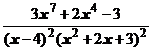 .
.
Вариант 13
1. Вычислить:
1) 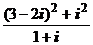 ; 2)
; 2) 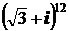 ; 3)
; 3) 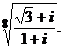
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+i+2|³ 3; 2) |z-i+1|< 1.
3. Разделить многочлен f(x)=4x4-2x3-16x2+5x+9 на многочлен g(x)=2x3-x2-5x+4 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
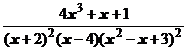 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
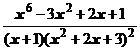 .
.
Вариант 14
1. Вычислить:
1) 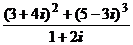 ; 2)
; 2) 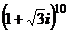 ; 3)
; 3) 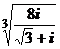 .
.
2. Описать множество комплексных чисел, удовлетворяющих неравенствам:
1) |z-i|> 1; 2) |z-i+3|£ 3.
3. Разделить многочлен f(x)=4x4-2x3-16x2+5x+9 на многочлен g(x)=2x3-x2-5x+4 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших:
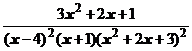 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
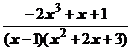 .
.
Вариант 15
1. Вычислить:
1) 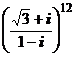 ; 2)
; 2) 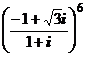 ; 3)
; 3) 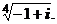
2. Описать множество комплексных чисел, удовлетворяющих неравенствам:
1) |z-2+3i|£ 3; 2) |z+i|> 4.
3. Разделить многочлен f(x)=x5-5x4-2x3+12x2-2x+12 на многочлен g(x)=x3-5x2-3x+17 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
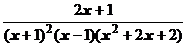 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
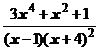 .
.
Вариант 16
1. Вычислить:
1) 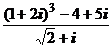 ; 2)
; 2) 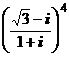 ; 3)
; 3) 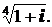
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+2i|£ 1; 2) |z+1+i|> 3.
3. Разделить многочлен f(x)=3x5+5x4-16x3-6x2-5x-6 на многочлен g(x)=3x4-4x3-x2-x-2 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
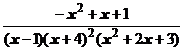 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
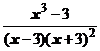 .
.
Вариант 17
1. Вычислить:
1) 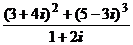 ; 2)
; 2) 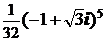 ; 3) 3)
; 3) 3) 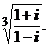
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z-2i-3|> 2; 2) |z+3i|£ 1.
3. Разделить многочлен f(x)=x4-x3-4x2+4x+1 на многочлен g(x)=x2-x-1 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
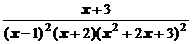 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
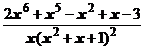 .
.
Вариант 18
1. Вычислить:
1) 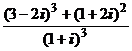 ; 2)
; 2) 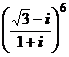 ; 3)
; 3) 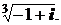
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+1+2i|³ 1; 2) |z-3i|< 3.
3. Разделить многочлен f(x)=3x3-2x2+x+2 на многочлен g(x)=x2-x+1 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
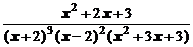 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
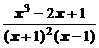 .
.
Вариант 19
1. Вычислить:
1) 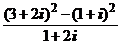 ; 2) 2)
; 2) 2) 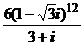 ; 3)
; 3) 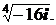
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+2i-3|> 2; 2) |z-3i|£ 3.
3. Разделить многочлен f(x)=3x7+6x6-3x5+4x4+14x3-6x2-4x+4 на многочлен g(x)=3x6-3x4+7x3-6x+2с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
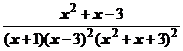 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
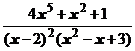 .
.
Вариант 20
1. Вычислить:
1) 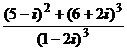 ; 2)
; 2) 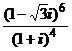 ; 3)
; 3) 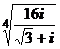 .
.
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+1+2i|³ 1; 2) |z-3i|< 3.
3. Разделить многочлен f(x)=x6-4x5+11x4-27x3+37x2-35x+35 на многочлен g(x)=x5-3x4+7x3-20x2+10x-25 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
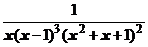 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
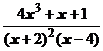 .
.
Вариант 21
1. Вычислить:
1) 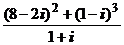 ; 2)
; 2) 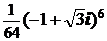 ; 3)
; 3) 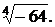
2. Описать множество комплексных чисел, удовлетворяющих неравенствам:
1) |z-i|> 1; 2) |z-i+3|£ 3.
3. Разделить многочлен f(x)=3x4-5x3+4x2-2x+1 на многочлен g(x)=3x3-2x2+x-1 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
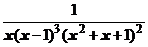 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
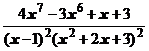 .
.
Вариант 22
1. Вычислить:
1) 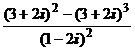 ; 2) 2)
; 2) 2) 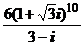 ; 3)
; 3) 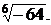
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+2i+3|< 2; 2) |z+3i|³ 3.
3. Разделить многочлен f(x)=3x7+6x6-3x5+2x4+10x3-4x2+3x+4 на многочлен g(x)=3x6-2x4-7x3-6x+4с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
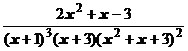 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
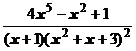 .
.
Вариант 23
1. Вычислить:
1) 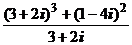 ; 2)
; 2) 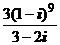 ; 3)
; 3) 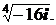
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z-3i-3|> 1; 2) |z+3i|£ 2.
3. Разделить многочлен f(x)=x7+6x6-3x5-3x4+9x3-6x2-4x+3 на многочлен g(x)=x6-2x4+7x3-4x+2 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
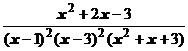 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
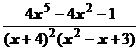 .
.
Вариант 24
1. Вычислить:
1) 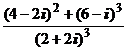 ; 2)
; 2) 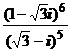 ; 3)
; 3) 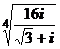 .
.
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+1-4i|³ 3; 2) |z+2-3i|< 2.
3. Разделить многочлен f(x)=2x6+3x5+8x4-27x3+3x2-5x+31 на многочлен g(x)=x5-2x4+4x3-2x2+10x-25 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
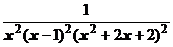 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
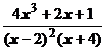 .
.
Вариант 25
1. Вычислить:
1) 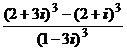 ; 2)
; 2) 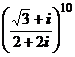 ; 3)
; 3) 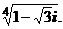
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+i-2|£ 4; 2) |z-4i|> 2.
3. Разделить многочлен f(x)=2x5-3x4-2x3+2x2-2x+1 на многочлен g(x)=x3-5x2-3x+7 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
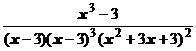 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
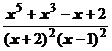 .
.
Вариант 26
1. Вычислить:
1) 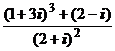 ; 2)
; 2) 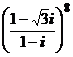 ; 3)
; 3) 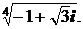
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+i+2|³ 4; 2) |z+1-3i|< 1.
3. Разделить многочлен f(x)=3x5-2x4-5x3+2x2-2x+5 на многочлен g(x)=x3-5x2+3x+12 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
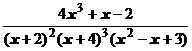 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
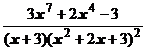 .
.
Вариант 27
1. Вычислить:
1) 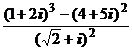 ; 2)
; 2) 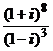 ; 3)
; 3) 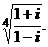
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z+2i+3|£ 4; 2) |z+2-3i|> 1.
3. Разделить многочлен f(x)=x4-2x3-3x2+1 на многочлен g(x)=x3+1 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
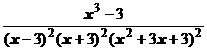 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
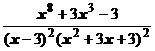 .
.
Вариант 28
1. Вычислить:
1) 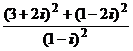 ; 2)
; 2) 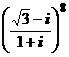 ; 3)
; 3) 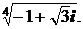
2. Описать геометрическое место комплексных чисел, удовлетворяющих неравенствам:
1) |z-2i+3|> 4; 2) |z-2+3i|£ 1.
3. Разделить многочлен f(x)=x6-4x5+10x4-27x3+3x2-5x+3 на многочлен g(x)=x5-3x4+7x3-2x2+10x-25 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
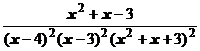 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
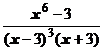 .
.
Вариант 29
1. Вычислить:
1) 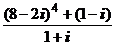 ; 2)
; 2) 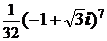 ; 3)
; 3) 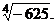
2. Описать геометрическое множество чисел, удовлетворяющих неравенствам:
1) |z+4-2i|£ 1; 2) |z-1-3i|> 3.
3. Разделить многочлен f(x)=x4-2x3-4x2+3x+1 на многочлен g(x)=x2-2x-1 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
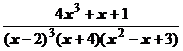 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
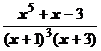 .
.
Вариант 30
1. Вычислить:
1) 
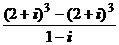 ; 2)
; 2) 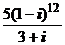 ; 3)
; 3) 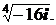
2. Описать множество комплексных чисел, удовлетворяющих неравенствам
1) |z-1-3i|£ 4 2) |z+2i|> 2.
3. Разделить многочлен f(x)=x5+5x4-16x3-6x2-5x-6 на многочлен g(x)=x4-4x3-x2-2x-2 с остатком. В ответе указать представление деления с остатком, (неполное) частное и остаток от деления.
4. Представить дробь в виде суммы простейших в общем виде и выписать систему линейных уравнений для определения коэффициентов:
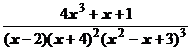 .
.
5. Представить дробь в виде суммы многочлена и простейших дробей:
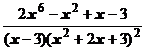 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|