
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
3. Изотермический процесс, Т=const. (закон Бойля – Мариотта)
Работа при расширении или сжатии газа
Найдем работу, которая совершается при расширении или сжатии газа, заключенного в сосуде с подвижным поршнем площадью 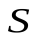 . Внешняя сила, действующая на поршень
. Внешняя сила, действующая на поршень 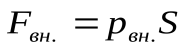 . При перемещении поршня вверх на малое расстояние
. При перемещении поршня вверх на малое расстояние  газ совершает элементарную работу
газ совершает элементарную работу 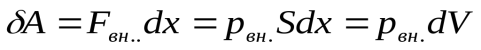 , где
, где 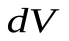 - изменение объема газа. Если изменение объема происходит квазистатически, то в любой момент времени газ находится в равновесном состоянии с внешней средой и его давление
- изменение объема газа. Если изменение объема происходит квазистатически, то в любой момент времени газ находится в равновесном состоянии с внешней средой и его давление 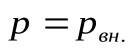 Элементарная работа газа в равновесном (квазистатическом) процессе изменения его объема:
Элементарная работа газа в равновесном (квазистатическом) процессе изменения его объема: 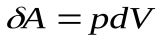 . Т. к.,
. Т. к., 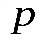 > 0, то при расширении газ совершает положительную работу. При сжатии
> 0, то при расширении газ совершает положительную работу. При сжатии 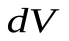 < 0, значит,
< 0, значит, 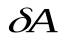 < 0 – работа газа отрицательна, положительную работу в этом случае совершают внешние силы.
< 0 – работа газа отрицательна, положительную работу в этом случае совершают внешние силы.
Если давление постоянное, то работа 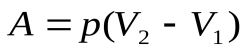 , при
, при 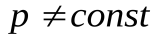 работа вычисляется как сумма элементарных работ, т. е., путем интегрирования:
работа вычисляется как сумма элементарных работ, т. е., путем интегрирования:
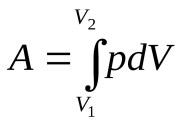 . Это численно равно площади под кривой
. Это численно равно площади под кривой 
 на соответствующем графике, рис. Эти выражения справедливы при любых изменениях объема твердых, жидких и газообразных тел.
на соответствующем графике, рис. Эти выражения справедливы при любых изменениях объема твердых, жидких и газообразных тел.
2. 5 Теплоемкость идеального газа
Из опыта следует, что внутренняя энергия идеального газа зависит только от температуры. Отсутствие зависимости 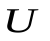 от объема газа указывает на то, что молекулы идеального газа не взаимодействуют друг с другом, иначе бы во внутреннюю энергию входило слагаемое, зависящее от расстояния между молекулами, т. е., от
от объема газа указывает на то, что молекулы идеального газа не взаимодействуют друг с другом, иначе бы во внутреннюю энергию входило слагаемое, зависящее от расстояния между молекулами, т. е., от 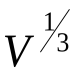 . Значит, подавляющую часть времени молекулы проводят в свободном полете.
. Значит, подавляющую часть времени молекулы проводят в свободном полете.
Теплоемкостью какого-либо тела называют величину, равную количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на 1К. Если сообщение телу тепла  повышает его температуру на
повышает его температуру на 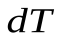 , то теплоемкость тела по определению:
, то теплоемкость тела по определению:  .
.
Теплоемкость единицы массы вещества называют удельной теплоемкостью:
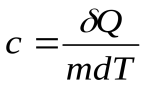 , тогда, молярная теплоемкость:
, тогда, молярная теплоемкость: 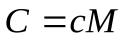 , а теплоемкость тела:
, а теплоемкость тела: 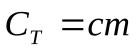 .
.
2. 6 Изопроцессы идеального газа
Уравнение первого закона термодинамики можно записать для равновесных процессов изменения его состояния в ином виде, используя выражения для теплоемкости однородного тела, откуда 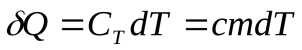 или с учетом молярной теплоемкости:
или с учетом молярной теплоемкости: 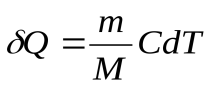 , а для одного моля
, а для одного моля 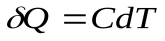 .
.
Тогда первый закон можно записать в виде:
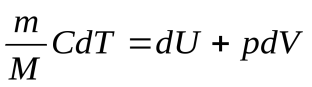
Применим его к различнымизопроцессам идеального газа.
- Изохорный процесс,
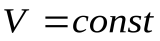 . (закон Шарля).
. (закон Шарля).
На диаграмме 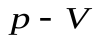 это вертикальная прямая: 1 – 2 нагрев, а 1 - 3 охлаждение. Практически этот процесс проводят, изменяя температуру газа, находящегося в толстостенном сосуде с неизменным объемом. В этом процессе работа не совершается:
это вертикальная прямая: 1 – 2 нагрев, а 1 - 3 охлаждение. Практически этот процесс проводят, изменяя температуру газа, находящегося в толстостенном сосуде с неизменным объемом. В этом процессе работа не совершается: 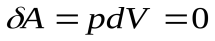 . Вся теплота идет на изменение его внутренней энергии.
. Вся теплота идет на изменение его внутренней энергии. 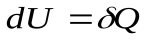 ,
,
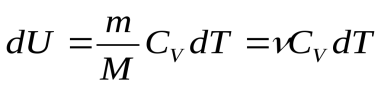 (1), где
(1), где 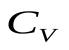 - молярная теплоемкость при постоянном объеме. Из опытов известно, что
- молярная теплоемкость при постоянном объеме. Из опытов известно, что 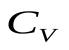 зависит от химического состава газа и его Т. Для не очень широкой области температур можно считать, что
зависит от химического состава газа и его Т. Для не очень широкой области температур можно считать, что 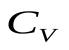 =const.
=const.
При изохорном конечном нагреве газа от температуры Т1 до температуры Т2 изменение внутренней энергии равно
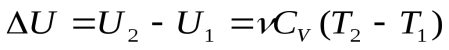 (2), и теплота, сообщенная системе:
(2), и теплота, сообщенная системе:
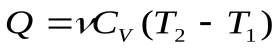 (3)
(3)
Для идеального газа внутренняя энергия это энергия теплового движения молекул, непосредственно не зависящая от объема (расстояния между молекулами), как в реальных газах. При расширении и сжатии газа его 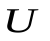 будет изменяться только за счет изменения кинетической энергии теплового движения, т. е., за счет температуры. Таким образом, соотношения (1) и (2) справедливы для любого процесса изменения состояния идеального газа, а не только изохорного. Внутренняя энергия газа зависит только от его массы, химического состава и температуры. Это подтверждается опытами Гей – Люссака и Джоуля.
будет изменяться только за счет изменения кинетической энергии теплового движения, т. е., за счет температуры. Таким образом, соотношения (1) и (2) справедливы для любого процесса изменения состояния идеального газа, а не только изохорного. Внутренняя энергия газа зависит только от его массы, химического состава и температуры. Это подтверждается опытами Гей – Люссака и Джоуля.
Значит, для любого равновесного процесса изменения состояния идеального газа уравнение первого закона термодинамики имеет вид:
 (4)
(4)
2. Изобарный процесс, 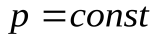 . ( Закон Гей -Люссака)
. ( Закон Гей -Люссака)
Он реализуется при нагревании газа в цилиндре с подвижным поршнем, на который действует постоянное внешнее давление.
На рис. изображены процессы изобарного расширения газа при его нагревании (1-2) и изобарного сжатия при его охлаждении (2-3).
Элементарная теплота, сообщенная газу в изобарном процессе:
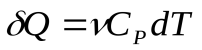 (5), где
(5), где 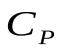 - молярная теплоемкость при постоянном давлении.
- молярная теплоемкость при постоянном давлении.
Элементарная работа, совершенная идеальным газом при этом:
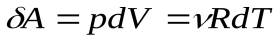 (6), учитывая уравнение Менделеева –Клапейрона.
(6), учитывая уравнение Менделеева –Клапейрона.
Из последнего уравнения можно выяснить смысл 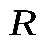 :
:
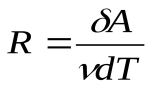 , т. е. универсальная газовая постоянная численно равна работе, совершенной одним молем идеального газа при его изобарном нагревании на 1К.
, т. е. универсальная газовая постоянная численно равна работе, совершенной одним молем идеального газа при его изобарном нагревании на 1К.
Подставим в первый закон выражения для  и
и 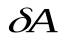 и найдем связь между
и найдем связь между 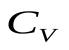 и
и 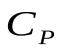 :
:
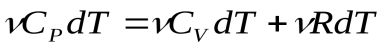 , откуда:
, откуда: 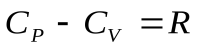 (7) – уравнение Майера для молярных теплоемкостей. Отсюда видно, что при изобарном нагревании газа к нему должна быть подведена большая теплота, чем для такого же изохорного нагревания, разность их равна работе, совершенной газом при изобарном расширении.
(7) – уравнение Майера для молярных теплоемкостей. Отсюда видно, что при изобарном нагревании газа к нему должна быть подведена большая теплота, чем для такого же изохорного нагревания, разность их равна работе, совершенной газом при изобарном расширении.
Работа газа при изобарном расширении при переходе из состояния 1 в состояние 2, рис.
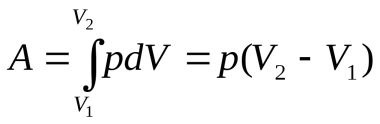 (8).
(8).
Если 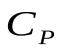 постоянная, то теплота, сообщенная газу в изобарном процессе:
постоянная, то теплота, сообщенная газу в изобарном процессе:
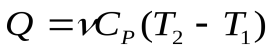 (9), а изменение внутренней энергии в процессе:
(9), а изменение внутренней энергии в процессе:
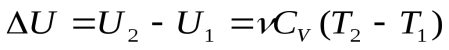 (10).
(10).
3. Изотермический процесс, Т=const. (закон Бойля – Мариотта)
Может происходить в условиях, когда теплообмен между газом и внешней средой осуществляется при постоянной (конечной) разности температур. Для этого теплоемкость внешней среды должна быть велика и процесс расширения или сжатия должен идти весьма медленно (для квазиравновесия). Изотермическими являются процессы кипения, конденсации, плавления и кристаллизации химически чистых веществ, происходящих при постоянном давлении.
Для идеального газа в этом процессе выполняется закон Бойля – Мариотта: 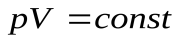 , графиком которого является гипербола, рис. . Внутренняя энергия газа постоянна в процессе, значит:
, графиком которого является гипербола, рис. . Внутренняя энергия газа постоянна в процессе, значит:
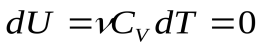 (11), а
(11), а 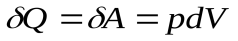 ,
,
т. е., вся теплота, сообщенная системе, идет на совершение газом работы против внешних сил:
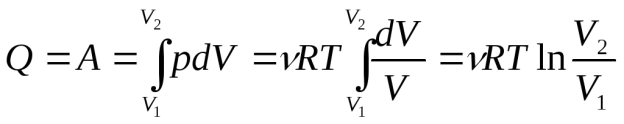 (12)
(12)
При изотермическом расширении  , к нему подводится теплота
, к нему подводится теплота  , газ совершает положительную работу,
, газ совершает положительную работу, 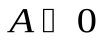 , рис. , процесс 1-2. При сжатии газа, процесс 1-3, работа, совершенная газом отрицательна, положительную работу при этом выполняют внешние силы, От газа отводится теплота
, рис. , процесс 1-2. При сжатии газа, процесс 1-3, работа, совершенная газом отрицательна, положительную работу при этом выполняют внешние силы, От газа отводится теплота 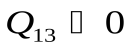 .
.
Теплоемкость газа в изотермическом процессе 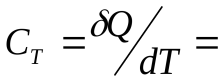 ±µ, т. к.,
±µ, т. к., 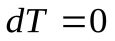 .
.
3. Адиабатный процесс, 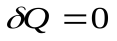 .
.
Это процесс, при котором система не обменивается теплотой с окружающей средой. Практически процесс производят при достаточно быстром расширении или сжатии газа.
Тогда из первого закона следует:
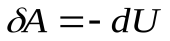 - система совершает работу за счет убыли внутренней энергии. Или, записывая более подробно, получим:
- система совершает работу за счет убыли внутренней энергии. Или, записывая более подробно, получим:
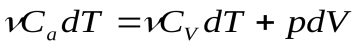 (13)
(13)
Здесь теплоемкость при адиабатном процессе - 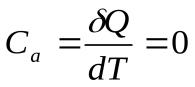 , т. к.,
, т. к., 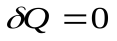 .
.
Из (13) видно, что 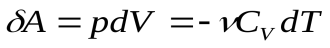 (14)
(14)
При расширении 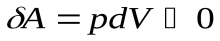 и
и 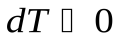 , газ охлаждается, при адиабатном сжатии
, газ охлаждается, при адиабатном сжатии  и
и 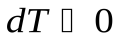 , газ нагревается.
, газ нагревается.
Связь между параметрами состояния адиабатного процесса можно найти, взяв дифференциалы от 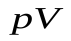 и от уравнения Менделеева - Клапейрона:
и от уравнения Менделеева - Клапейрона:
 (15), отсюда можно выразить
(15), отсюда можно выразить 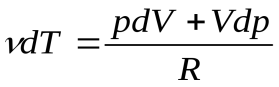 , подставить в уравнение (14) и получить:
, подставить в уравнение (14) и получить: 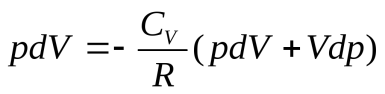 . Заменив здесь
. Заменив здесь 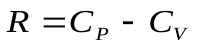 из уравнения Майера, получим после простых преобразований:
из уравнения Майера, получим после простых преобразований:
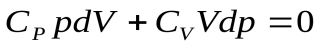 , далее разделим переменные, поделив уравнение на
, далее разделим переменные, поделив уравнение на 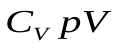 и обозначим
и обозначим  - показатель адиабаты или постоянная Пуассона.
- показатель адиабаты или постоянная Пуассона.
Тогда 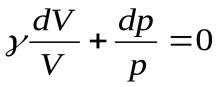 . После интегрирования
. После интегрирования 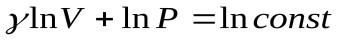 или:
или:
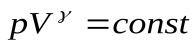
Это есть уравнение адиабаты или уравнение Пуассона. С помощью уравнения Менделеева – Клапейрона его можно записать через другие параметры:
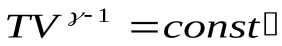 или
или 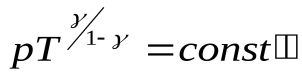 .
.
Из рис. видно, что адиабата идет круче, чем изотерма, поскольку 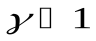 для любого идеального газа. Это объясняется тем, что при адиабатном сжатии увеличение давления происходит не только из-за уменьшения объема, как в изотермическом процессе, но и из-за возрастания температуры. При адиабатном расширении газа его температура уменьшается и давление падает сильнее, чем при соответствующем изотермическом расширении.
для любого идеального газа. Это объясняется тем, что при адиабатном сжатии увеличение давления происходит не только из-за уменьшения объема, как в изотермическом процессе, но и из-за возрастания температуры. При адиабатном расширении газа его температура уменьшается и давление падает сильнее, чем при соответствующем изотермическом расширении.
Работа в адиабатном (конечном) процессе 1-2 ( на рис. площадь под кривой)
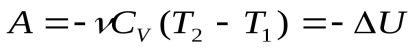
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|