
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Розв’язання.
ВІННИЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
КАФЕДРА ПРИКЛАДНОЇ МАТЕМАТИКИ
ТИПОВІ РОЗРАХУНКИ № 1
з вищої математики
Тема: " Лінійна й векторна алгебра.
Аналітична геометрія. "
Варіант № 351
Викон.: ст. гр. АТ-09
ДИМИТРЕНКО О. І.
Вінниця 2009 р.
Задача № 1. Розв'язати систему лінійних рівнянь трьома методами: методом Крамера, матричним методом та методом Гаусса.
Матричний метод.
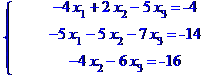
Матриця коефіцієнтів системи рівнянь
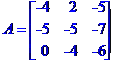
Стовпець вільних членів
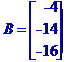
Стовпець невідомих
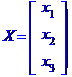
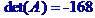
Детермінант матриці системи відмінний від нуля, отже система має розв'язок.
Розв'яжемо ситему лінійних рівняь матричним методом.
Обчислимо алгебраїчні доповнення елементів матриці А
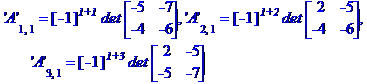
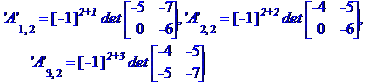
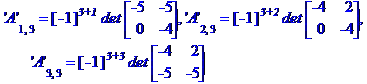
Знаходимо обернену матрицю коефіцієнтів системи рівнянь
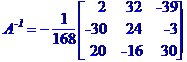
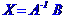
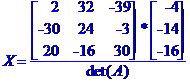
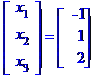
Метод Крамера розв'язання системи лінійних алгебраїчних рівнянь
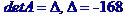
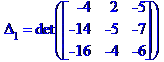
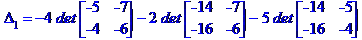
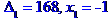
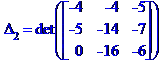
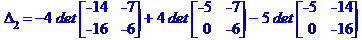
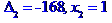
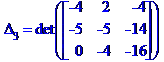
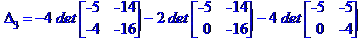
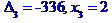
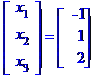
Метод Гаусса
Прямий хід методу виключення Гауса - схема єдиного ділення.
Вихідні дані
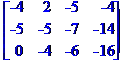
Крок1
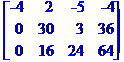
Крок1. 1
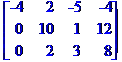
Крок2
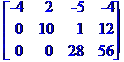
Крок2. 1
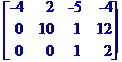
Вихідні дані
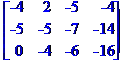
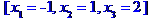
Задача № 1. 2. Розв'язати систему лінійних рівнянь трьома методами: методом Крамера, матричним методом та методом Гаусса.
Розв'язати систему лінійних рівнянь методом Гаусса
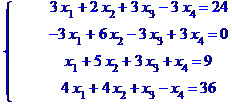
Прямий хід методу виключення Гауса - схема єдиного ділення.
Ділимо рівняння № 2 на 3.
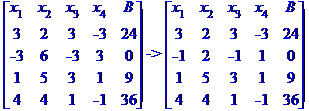
Крок 1

Ділимо рівняння № 1 на 8.
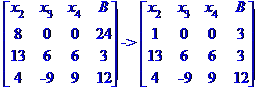
Крок 2
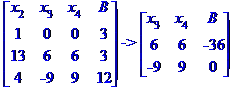
Ділимо рівняння № 1 на 6.
Ділимо рівняння № 2 на 9.
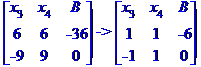
Крок 3
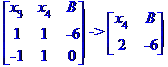
Ділимо рівняння № 1 на 2.
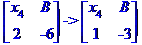
Обернений хід
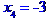
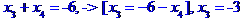
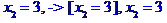
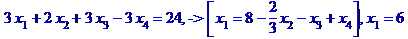
Відповідь
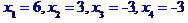
МАТРИЧНИЙ МЕТОД. МАТРИЧНИЙ МЕТОД. МАТРИЧНИЙ МЕТОД.
---------------------------------------------------
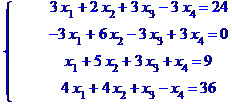
Матриця коефіцієнтів системи рівнянь

Стовпець вільних членів
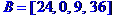
Стовпець невідомих
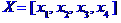
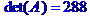
Детермінант матриці системи відмінний від нуля, отже система має розв'язок.
Розв'яжемо ситему лінійних рівняь МАТРИЧНИМ МЕТОДОМ.
Обчислимо алгебраїчні доповнення елементів матриці А
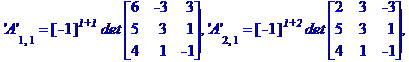
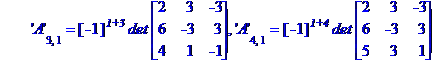
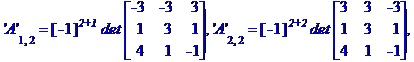
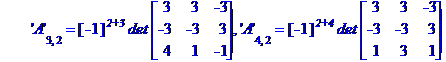
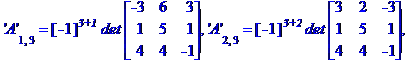
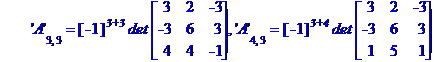
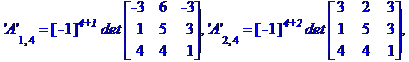
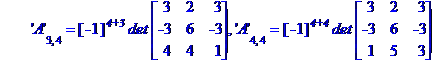
Знаходимо обернену матрицю коефіцієнтів системи рівнянь
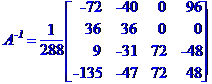
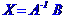
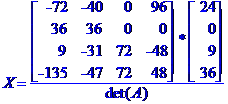
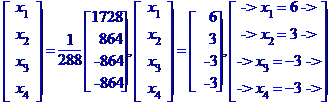
МЕТОД КРАМЕРА. МЕТОД КРАМЕРА. МЕТОД КРАМЕРА
---------------------------------------------------
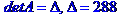
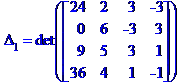
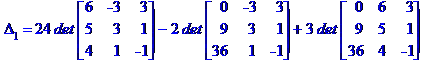
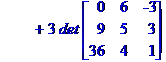
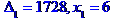

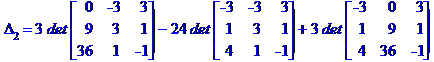
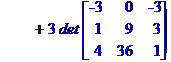
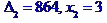

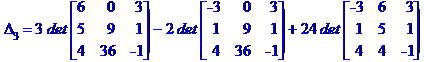
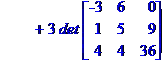
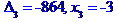

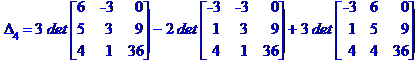

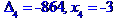
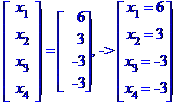
Задача № 2. Знайти всі розв'язки системи двох лінійних рівнянь з трьома невідомими.
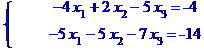

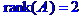

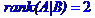
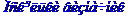
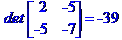

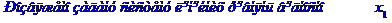
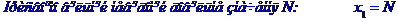

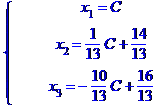
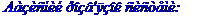
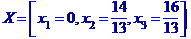
Задача № 3.
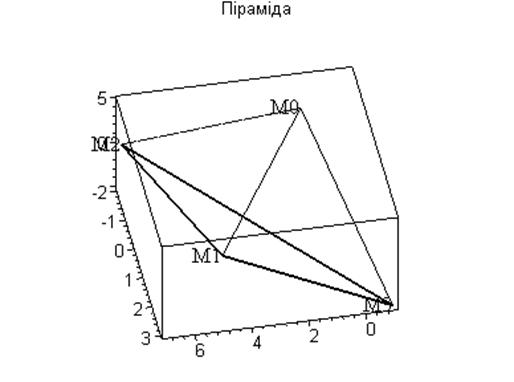
Задані координати вершин піраміди M0, М1, М2, М3.
Знайти:
1) довжину ребра М0М1;
2) кут між ребрами М0М1 та М0М3;
3) кут між ребром М0М3 та гранню М0М1М2;
4) площу грані М0М1М2;
5) об'єм піраміди;
6) рівняння прямої М0М1;
7) Рівняння площини М0М1М2;
8) рівняння висоти піраміди, яка проходить через вершину М3.
Зробити креслення.
Розв’язання.

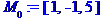
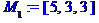
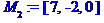
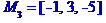

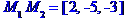
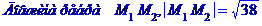

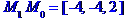
Кут між ребрами 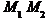 та
та 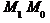 :
: 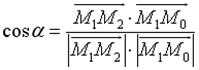
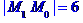
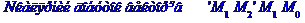
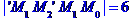
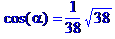

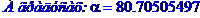
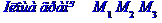
дорівнює модулю векторного добутку векторів 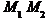 та
та 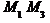 :
: 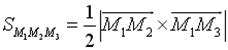
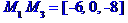
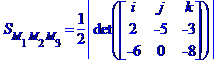
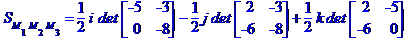
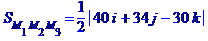
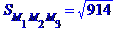
дорівнює одній шостій модуля мішаного добутку векторів 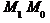 ,
, 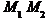 та
та 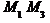 :
:
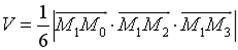
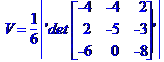
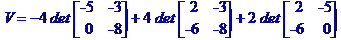
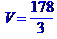
Рівняння ребра 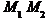 в канонічній формі має вид
в канонічній формі має вид 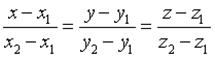
або 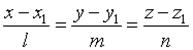 . В параметричній формі:
. В параметричній формі:
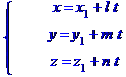
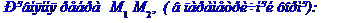

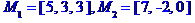
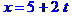
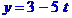
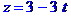
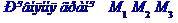

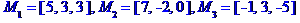
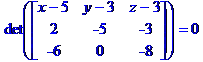

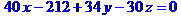
Кутом 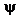 між прямою і площиною називається гострий кут між прямою та її проекцією на площину. Цей кут можна обчислити за формулою
між прямою і площиною називається гострий кут між прямою та її проекцією на площину. Цей кут можна обчислити за формулою

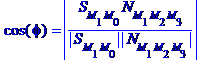
де 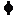 - кут між прямою та нормальним вектором площини.
- кут між прямою та нормальним вектором площини.
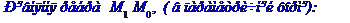
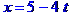
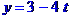
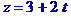
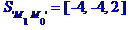
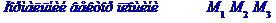
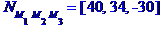
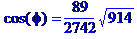
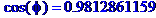
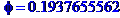
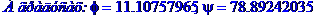
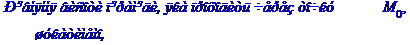
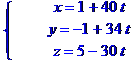
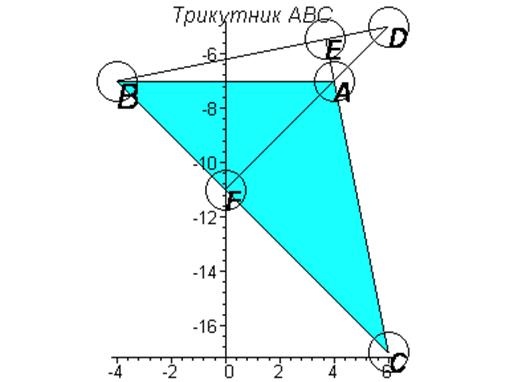
Задача № 4.
Дано дві вершини A(4; -7) і B(-4; -7) та точка D(6; -5) перетину висот трикутника. Скласти рівняння його сторін. Зробити креслення.
Розв’язання.
Позначимо задані координати так:
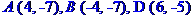
Рівняння сторони АВ запишемо як рівняння прямої, що проходить через дві задані точки 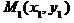 та
та 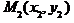 :
:
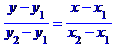
За точки 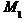 та
та 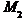 візьмемо точки A та B
візьмемо точки A та B
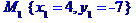
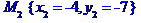
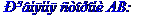
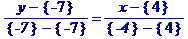
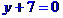
Запишемо рівняння висот трикутника, що виходять з вершин А та В як рівняння прямих, що проходить через дві задані точки 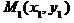 та
та 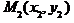 . За точки
. За точки 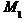 та
та 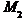 беремо відповідно точки A, D та точки B, D.
беремо відповідно точки A, D та точки B, D.
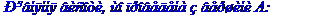
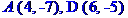
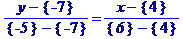
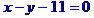
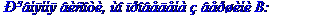
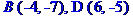
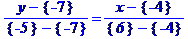
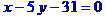
Рівняння сторони ВС запишемо як рівняння прямої, яка проходить через т. В перпендикулярно до висоти, проведеної з вершини А. Рівняння прямої, що проходить через т. M(x[1], y[1]) перпендикулярно до прямої y=k[1]*x+b[1], має вигляд
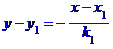
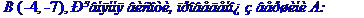
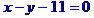
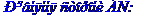
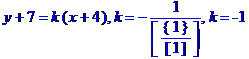
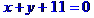
Рівняння сторони АС запишемо як рівняння прямої, яка проходить через т. А перпендикулярно до висоти, проведеної з вершини В

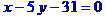
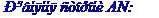
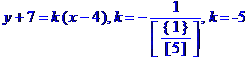
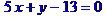
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|