Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Действия со случайными событиями

Билет№1

Теория вероятностей —наука, занимающаяся анализом математических моделей для принятия решений в условиях неопределенности.

Предметом теории вероятностей является количественный и качественный анализ математических моделей вероятностных экспериментов, называемый статической обработкой экспериментальных данных.

Билет№2

Множество всех элементарных событий, имеющих место в результате случайного эксперимента, будем называть пространством элементарных событий W (элементарное событие соответствует элементарному исходу). Случайными событиями, будем называть подмножества пространства элементарных событий W.

Билет№3

Статистическое определение. Вероятностью события 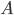называется число, относительно которого стабилизируется (устанавливается) относительная частота 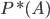при неограниченном увеличении числа опытов. В практических задачах за вероятность события 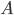принимается относительная частота 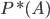при достаточно большом числе испытаний. Из данных определений вероятности события 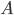видно, что всегда выполняется неравенство

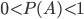
Для определения вероятности события на основе формулы 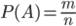 часто используются формулы комбинаторики, по которым находится число благоприятствующих исходов и общее число возможных исходов.

Виды случайных событий:

События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Билет№4

Действия со случайными событиями

Суммой событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одному из событий A или B. Обозначается A + B.

Произведением событий A и B называется событие, состоящее из всех элементарных событий, принадлежащих одновременно событиям A и B. Обозначается AB.

Разностью событий A и B называется событие, состоящее из всех элементарных событий принадлежащих A, но не принадлежащих B. Обозначается A\B.

(виды случайных соб-ий в билете №3).

Билет№5

Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:

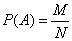
Это определение вероятности часто называют классическим.

Билет№6

Пусть задано пространство элементарных событий Е, а вероятности Р определены на событиях из Е. Тогда:

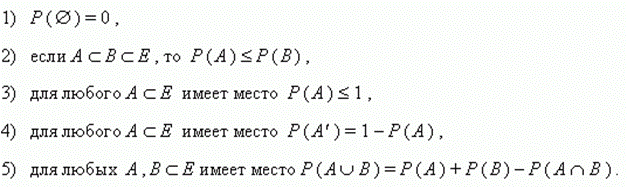
Билет№7

Размещениями из n элементов по k элементов будем называть упорядоченные подмножества, состоящие из k элементов множества 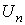(множества, состоящего из n элементов). Число размещений из n элементов по k элементов обозначается 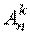(читается " А из n по k" ):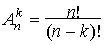

Число сочетаний из n элементов по k элементов обозначается 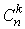(читается " C из n по k" ):  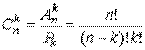                                где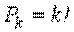

Билет№8

События А и В называются независимыми, если .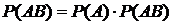

Свойство. События А и В независимы тогда и только тогда когда P(B/A)=P(B).

.

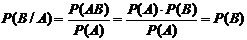Пусть P(B/A)=P(B), тогда 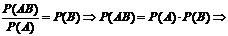 А и В независимы.

Билет№9

Условной вероятностью события A по отношению к событию B называется вероятность события A, вычисленная при условии, что событие B произошло. Обозначается: P(A|B) (кратко читается так: “P от A при условии B”). Условная вероятность обладает всеми свойствами безусловной вероятности. В частности, P(A|B) + P( A |B) = 1. Отметим также, что если B ⊂ A, то P(A|B) = 1; если AB = V, то P(A|B) = 0.

Билет№10

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:

р (АВ) = р (А) · р (В/А).

Если подобным образом вычислить вероятность события ВА, совпадающего с событием АВ, то получим, что р (ВА) = р (В) · р (А/В). Следовательно,

р (А) · р (В/А) = р (В) · р (А/В).

Белет№11

Если события Н₁, Н₂, …, Н_n образуют полную группу, то вероятность любого события А можно вычислить по формуле полной вероятности:

,

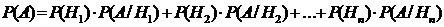или .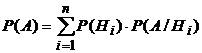

Пусть события Н₁, Н₂, …, Н_n образуют полную группу, А–некоторое событие, причем P(A)≠ 0, тогда имеет место формула Байеса:

,

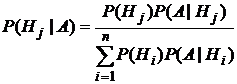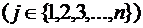
Билет№12                                                                            

Проводится серия из n испытаний, в каждом из которых с вероятностью р может произойти событие А, с вероятностью q=1-р событие .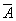

Вероятность наступления события А не зависит от числа испытаний n и результатов других испытаний.

Такая схема испытаний с двумя исходами (событие А наступило либо не наступило) называется схемой последовательных испытаний Бернулли.

Билет№13

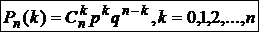—формула Бернулли.

Билет№14

Если вероятность р появления события А в каждом испытании при неограниченном возрастании числа испытаний n изменяется таким образом, что некоторое событие А появится ровно k раз в n независимых испытаниях стремится к величине 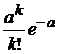, то есть .

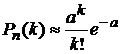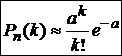—формула Пуассона.

Билет№15

Если вероятность появления события А в каждом отдельном испытании постоянная и отлична от 0 и 1, т. е. 0< p< 1, то вероятность того, что событие А появится ровно k раз в n независимых испытаниях.

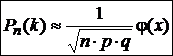                                                      , где 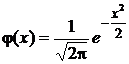; 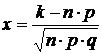, q=1-p.

Имеются специальные таблицы значений функций φ (х). Нужно учитывать, что функция φ (х)–четная, т. е. φ (х)=φ (-х).

Билет№16

Если вероятность появления события А в каждом отдельном испытании постоянна и отлична от 0 и 1, т. е. 0< p< 1, то вероятность того, что событие А появится от k₁ до k₂ раз в n независимых испытаниях определяется выражением:

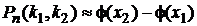, где

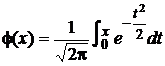—функция Лапласа,

, , .

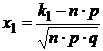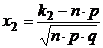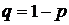Функция Лапласа—нечетная, т. е. 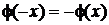. Значения находят по таблице.

Билет№18

Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов 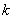(появлений события) имеет вид:

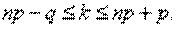
Так как 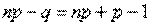, то эти границы отличаются на 1. Поэтому 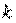, являющееся целым числом, может принимать либо одно значение, когда 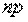целое число ( 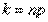), то есть когда 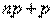(а отсюда и 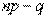) нецелое число, либо два значения, когда 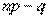целое число.

Билет№19

Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причём заранее не известно, какое именно значение она примет. Случайные величины обозначают большими латинскими буквами (X, Y, Z1, …), а их возможные значения – соответствующими малыми буквами (x, y, z, …). Событие, состоящее в том, что случайная величина X примет значение x, будем отражать записью X = x. С левой стороны этого равенства стоит имя случайной величины, а справа – прини-маемое ею значение. Вероятность этого события будем обозначать P{X = x}. Аналогично, P{X < x} – вероятность того, что случайная величина X примет значение, меньшее, чем x.  

Билет№20

Случайная величина Х называется дискретной, если она принимает конечное либо счетное число значений, т. е. Ω х—конечно или счетно.

Законом распределения дискретной случайной величины Х называется совокупность пар чисел вида (х_i, р_i), где x_i—возможные значения случайной величины, а p_i—вероятности, с которыми случайная величина принимает эти значения, т. е. 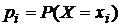, причем .

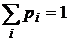Билет№22

Свойство1. Функция распределения F(x)–неубывающая функция, т. е. для 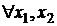 таких что x₁< x₂ .

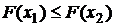Замечание. Если функция распределения F(x) непрерывная, то свойство выполняется и при замене знаков ≤ и < на < и ≤.

Свойство 2. , .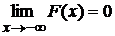

, .

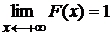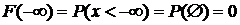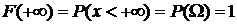Свойство 3. Функция F(x) непрерывна слева. (т. е. ).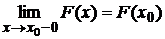

Свойство 4. Вероятность того, что значение случайной величины Х больше некоторого числа х, вычисляется по формуле.

.

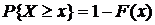Билет№23

Распределение случайной величины 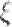называется непрерывным, а сама случайная величина - непрерывной случайной величиной, если для любого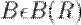

,

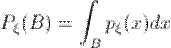где 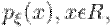- интегрируемая по Лебегу функция. Функция 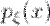называется плотностью распределения случайной величины .

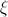Теорема : Для того чтобы случайная величина 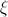была непрерывной случайной величиной, необходимо и достаточно, чтобы для любого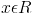         

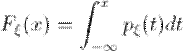
Билет№24

Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f(x).

Основные свойства плотности распределения:

1. Плотность распределения неотрицательна: f(x) > 0.

Это свойство следует из определения f(x) – производная неубывающей функции не может быть отрицательной.

2. Условие нормировки: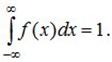

Билет№25

Биноминальное распределение - это распределение вероятностей возможных чисел появления события А при n независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А) = р = const. Кроме события А может произойти также противоположное событие Ā, вероятность которого Р(Ā ) = 1 - р = q.

Билет№26

Распределение Пуассона - это дискретное распределение, являющееся одним из важных предельных случаев биномиального распределения. При росте n и зафиксированном значении произведения np=λ > 0 биномиальное распределение B(n, p) сходится к распределению Пуассона. Таким образом, случайная величина, имеющая распределение Пуассона с параметром λ , принимает неотрицательные целые значения с вероятностью 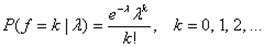     Интегральная функция вероятности распределения равна 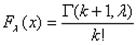Параметр λ является одновременно и математическим ожиданием, и дисперсией случайной величины, имеющей распределение Пуассона.

Классическим примером случайной величины, распределенной по Пуассону, является количество машин, проезжающих через какой-либо участок дороги за заданный период времен.

Билет№21

Функцией распределения случайной величины Хназывается функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х примет в результате эксперимента значение, меньшее некоторого фиксированного числа х.

.

.

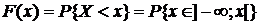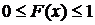Если рассматривать Х как случайную точку на оси ох, то F(x) с геометрической точки зрения—это вероятность того, что случайная точка Х в результате реализации эксперимента попадет левее точки х.

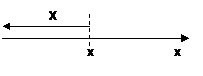
Билет№27

Дискретное равн-ое распред-ие: Говорят, что случайная величина X распределена по равномерному закону, если она может принимать только целые неотрицательные значения от 1 до n, а вероятности всех возможных значений одинаковы. Таким образом,

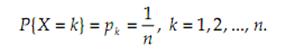
Непрерывное равн-ое распред-ие: Говорят, что случайная величина X распределена равномерно в интервале [a, b], если её плотность распределения вероятностей определяется формулой:

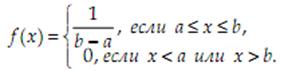
Соответствующая функция распределения вероятностей имеет следующий вид: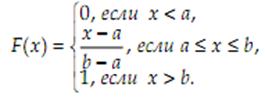

Билет№28

Говорят, что случайная величина X распределена по нормальному закону, если её плотность распределения вероятностей определяется следующей формулой:

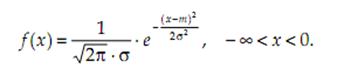
Соответствующая функция распределения вероятностей имеет следующий вид:

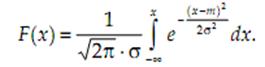
Билет№29

Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргу-мента Х: Y=φ (X).

  Билет 30Рассмотрим случайную величину *, возможные значения которой образуют конечную или бесконечную последовательность чисел x1, x2, ..., xn, ... . Пусть задана функция p(x), значение которой в каждой точке x=xi (i=1, 2, ... ) равно вероятности того, что величина примет значение xi. 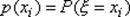. Такая случайная величина называется дискретной (прерывной). Функция р(х) называется законом распределения вероятностей случайной величины, или кратко, законом распределения. Эта функция определена в точках последовательности x1, x2, ..., xn, ... . Так как в каждом из испытаний случайная величина принимает всегда какое-либо значение из области ее изменения, то 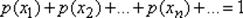. Пример. Пусть случайная величина - число наступления события A при одном испытании, причем P(A)=p. Множество возможных значений состоит из 2-х чисел 0 и 1: =0, если событие A не произошло, и =1, если событие A произошло. Таким образом, 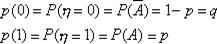Предположим, что производится n независимых испытаний, в результате каждого из которых может наступить или не наступить событие A. Пусть вероятность наступления события A при каждом испытании равна p. Рассмотрим случайную величину  — число наступлений события A при n независимых испытаниях. Область изменения  состоит из всех целых чисел от 0 до n включительно. Закон распределения вероятностей р(m) определяется формулой Бернулли (13'): 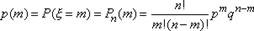. Закон распределения вероятностей по формуле Бернулли часто называют биномиальным, так как Pn(m) представляет собой m-й член разложения бинома 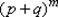Пусть случайная величина  может принимать любое целое неотрицательное значение, причем 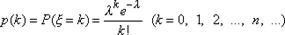где 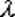— некоторая положительная постоянная. В этом случае говорят, что случайная величина распределена по закону Пуассона, Заметим, что при k=0 следует положить 0! =1.

Билет 31 Непрерывные случайные величины.    Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины: 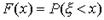. Таким образом, и здесь функция F(х) определена на всей числовой оси, и ее значение в точке х равно вероятности того, что случайная величина примет значение, меньшее чем х. Случайная величина  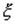называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* 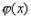, удовлетворяющая для любых значений x равенству 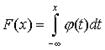. Функция  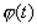называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x1< x2, то имеем 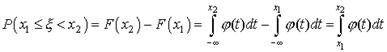Так как , а на основании формулы (22) 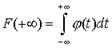. То 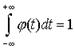 . Пользуясь формулой (22), найдем 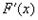как производную интеграла по переменной верхней границе, считая плотность распределения 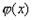непрерывной**:  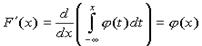. Заметим, что для непрерывной случайной величины функция распределения F(х) непрерывна в любой точке х, где функция  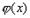непрерывна. Это следует из того, что F(х) в этих точках дифференцируема. На основании формулы (23), полагая x1=x, 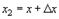, имеем 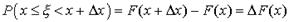. В силу непрерывности функции F(х) получим, что 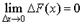. Следовательно 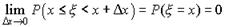. Таким образом, вероятность того, что непрерывная случайная величина может принять любое отдельное значение х, равна нулю.

Билет 32 Математи́ ческое ожида́ ние — среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей. [1] Математическое ожидание). В статистике часто используют обозначение μ. Определение: Пусть задано вероятностное пространство 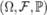 и определённая на нём случайная величина X. То есть, по определению,  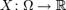— измеримая функция. Если существует интеграл Лебега от X по пространству Ω, то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается M[X] или  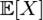.  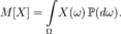    Основные формулы для математического ожидания: Если FX(x) — функция распределения случайной величины, то её математическое ожидание задаётся интегралом Лебега — Стилтьеса:  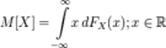     . Свойства математического ожидания: 1)Математическое ожидание числа есть само число M[a] = a.  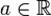— константа; 2) Математическое ожидание линейно, то есть M[aX + bY] = aM[X] + bM[Y], где X, Y — случайные величины с конечным математическим ожиданием, а  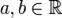— произвольные константы. 3) Математическое ожидание сохраняет неравенства, то есть если  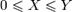. почти наверное, и Y — случайная величина с конечным математическим ожиданием, то математическое ожидание случайной величины X также конечно, и более того  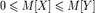. 4) Математическое ожидание не зависит от поведения случайной величины на событии вероятности нуль, то есть если X = Y почти наверное, то M[X] = M[Y]. 5) Математическое ожидание произведения двух независимых случайных величин X, Y равно произведению их математических ожиданий M[XY] = M[X]M[Y].

Билет 33 Дисперсией 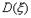 случайной величины 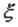называется математическое ожидание квадрата отклонения случайной величины от ее математичекого ожидания *: 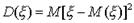. Пусть  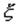- дискретная случайная величина, принимающая значения x1, x2, ..., xn соответственно с вероятностями p1, p2, ..., pn. Очевидно, случайная величина  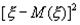принимает значения 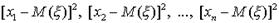. с теми же вероятностями p1, p2, ..., pn. Следовательно, согласно определению математического ожидания дискретной случайной величины, имеем  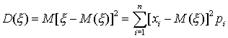. Если же  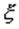- случайная величина с плотностью распределения 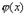, то по определению 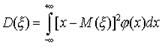. Принимая во внимание определение дисперсии и свойства математического ожидания, имеем 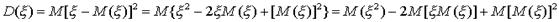. Так как и - постоянные, то используя свойства математического ожидания, получим 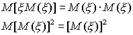. Следовательно, 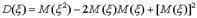. Откуда окончательно находим 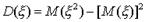. Рассмотрим теперь свойства дисперсии:  1). Дисперсия постоянной равна нулю. 2). Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: 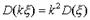. 3). Если и - независимые случайные величины, то дисперсия суммы этих величин равна сумме их дисперсий: 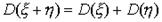. Средним квадратическим отклонением 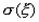случайной величины  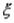называется корень квадратный из ее дисперсии: 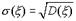. Среднее квадратическое отклонение 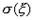имеет ту же размерность, что и случайная величина .

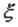Билет 35Моме́ нт случа́ йной величины́ — числовая характеристика распределения данной случайной величины. Определения: Если дана случайная величина 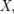 определённая на некотором вероятностном пространстве, то: 1) -м нача́ льным моментом случайной величины 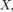 где 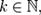 называется величина  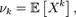если математическое ожидание  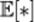в правой части этого равенства определено; 2)  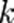-м центра́ льным моментом случайной величины  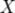называется величина  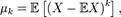 3) -м абсолю́ тным и -м центральным абсолютным моментами случайной величины 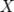называется соответственно величины  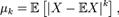     4) -м факториальным моментом случайной величины 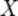называется величина  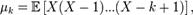если математическое ожидание в правой части этого равенства определено. Абсолютные моменты могут быть определены не только для целых k, но и для любых положительных действительных в случае, если соответствующие интегралы сходятся.   Вычисление моментов: 1)Моменты могут быть вычислены напрямую через определение путём интегрирования соответствующих степеней случайной величины. В частности, для абсолютно непрерывного распределения с плотностью 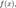имеем:  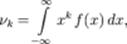. если  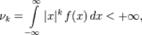а для дискретного распределения с функцией вероятност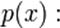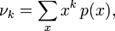и  если 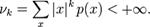                             2) Также моменты случайной величины могут быть вычислены через ее характеристическую функцию 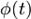:  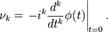           3)Если распределение таково, что для него в некоторой окрестности нуля определена производящая функция моментов  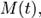то моменты могут быть вычислены по следующей формуле: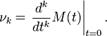

Билет 36 Ковариа́ ция (корреляционный момент) в теории вероятностей и математической статистике мера линейной зависимости двух случайных величин. Определение: Пусть X, Y — две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда их ковариация определяется следующим образом: 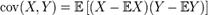. в предположении, что все математические ожидания E в правой части определены. Ковариация выборок: Пусть X1, X2,..., Xn, Y1, Y2,..., Yn — выборки X(n), Y(n) случайных величин, определенных на одном и том же вероятностном пространстве. Тогда ковариацией между выборками X(n) и Y(n) является  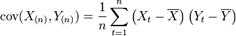. где 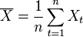 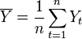— среднее значение выборок. Очевидно, что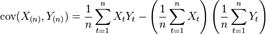

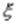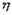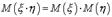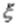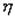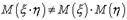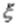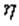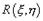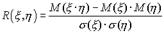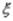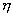Билет 37  если и  - независимые случайные величины, то по свойству математического ожидания . Если же  и  не являются независимыми случайными величинами, то, вообще говоря, . Условились за меру связи (зависимости) двух случайных величин и принять безразмерную величину , определяемую соотношением.    и называемую коэффициентом корреляции. Свойства коэффициента корреляции: Если и  - независимые случайные величины, то коэффициент корреляции равен нулю.

Билет 38  Определение: Случайные величины  называют независимыми (в совокупности), если для любого набора борелевских множеств 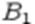, ...,  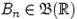 имеет место равенство: 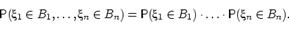Определение: Случайные величины 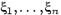называют попарно независимыми, если независимы любые две из них. Определение:  Случайные величины 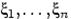независимы (в совокупности), если для любых 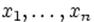имеет место равенство: 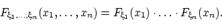Определение: Случайные величины  с дискретным распределением независимы (в совокупности), если для любых чисел 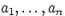имеет место равенство: 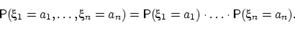Определение:   Случайные величины 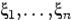с абсолютно непрерывным совместным распределением независимы (в совокупности), если плотность совместного распределения равна произведению плотностей случайных величин 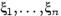, т. е. для любых  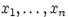имеет место равенство: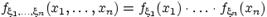

Билет 39  Нера́ венство Чебышёва в теории вероятностей утверждает, что случайная величина в основном принимает значения близкие к своему среднему. Более точно, оно даёт оценку вероятности, что случайная величина примет значение далёкое от своего среднего. Неравенство Чебышёва является следствием. Пусть случайная величина 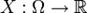определена на вероятностном пространстве 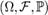, и её математическое ожидание μ и дисперсия σ 2 конечны. Тогда  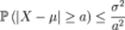    где a > 0. Если a = kσ, где σ - стандартное отклонение и k > 0, то получаем  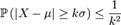  В частности, случайная величина с конечной дисперсией отклоняется от среднего больше, чем на 2 стандартных отклонения с вероятностью меньше 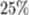. Она отклоняется от среднего на 3 стандартных отклонения с вероятностью меньше 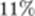. Следствие: (обобщённое неравенство Чебышёва). Пусть функция  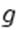не убывает и неотрицательна на 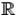. Если 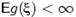, то для любого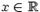 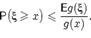        Следствие: (неравенство Чебышёва — Бьенеме). Если 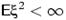, то для любого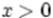 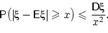    Следствие 19. Если 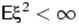, то.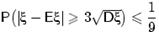

Билет40 Основными понятиями теории вероятностей являются понятия случайного события и случайной величины. При этом предсказать заранее результат испытания, в котором может появиться или не появиться то или иное событие или какое-либо определенное значение случайной величины, невозможно, так как исход испытания зависит от многих случайных причин, не поддающихся учету. Однако при неоднократном повторении испытаний наблюдаются закономерности, свойственные массовым случайным явлениям. Эти закономерности обладают свойством устойчивости. Суть этого свойства состоит в том, что конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате большой массы подобных явлений, а характеристики случайных событий и случайных величин, наблюдаемых в испытаниях, при неограниченном увеличении числа испытаний становятся практически не случайными. Пусть производится большая серия однотипных опытов. Исход каждого отдельного опыта является случайным, неопределенным. Однако, несмотря на это, средний результат всей серии опытов утрачивает случайный характер, становится закономерным. Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. Под законом больших чисел не следует понимать какой-то один общий закон, связанный с большими числами. Закон больших чисел - это обобщенное название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным. К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли - простейшим. В основе доказательства теорем, объединенных термином " закон больших чисел", лежит неравенство Чебышева, по которому устанавливается вероятность отклонения от ее математического ожидания: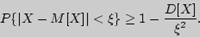

Билет 41Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения. Классическая формулировка Ц. П. Т. Пусть 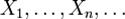есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние μ и σ 2, соответственно.  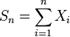 тогда 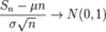 по распределению при 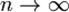, где N(0, 1) — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом выборочное среднее первых n величин, то есть 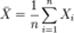, мы можем переписать результат центральной предельной теоремы в следующем виде:  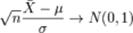. по распределению при 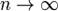.                            Нормальное распределение, также называемое гауссовским распределением или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения: 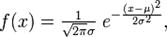где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ ² — дисперсия. Нормальное распределение играет важнейшую роль во многих областях знаний, особенно в статистической физике. Физическая величина, подверженная влиянию значительного числа независимых факторов, могущих вносить с равной погрешностью положительные и отрицательные отклонения, вне зависимости от природы этих случайных факторов, часто подчиняется нормальному распределению, поэтому из всех распределений в природе чаще всего встречается нормальное (отсюда и произошло одно из названий этого распределения вероятностей). Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).