
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Алгебра
17. 11. 2021
10 класс
Алгебра
Тема: " Степень с рациональным и действительным показателем"
Вспомним свойства арифметического корня:

Разбираем новую тему
Посмотрите видеоурок
https: //www. youtube. com/watch? v=ZoWXq8lxYfY
Прочитайте материал урока
Е сли n — натуральное число, причём 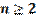 , m — целое число и частное
, m — целое число и частное  является целым числом, то при a> 0 справедливо равенство
является целым числом, то при a> 0 справедливо равенство 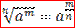 .
.
Таким образом, формула 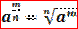 справедлива для любого целого числа m и любого натурального числа
справедлива для любого целого числа m и любого натурального числа 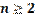 и положительного основания степени
и положительного основания степени 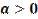 .
.
Например, 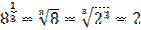
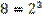
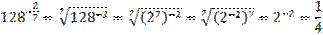
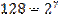 .
.
Напомним, что рациональное число  – это число вида
– это число вида  , где
, где 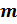 – целое,
– целое,  – натуральное число. Тогда по формуле
– натуральное число. Тогда по формуле 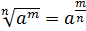 получаем
получаем 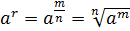 .
.
Таким образом, степень определена для любого рационального показателя r и любого положительного основания а.
Пользуясь формулой 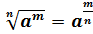 , степень с рациональным показателем можно представить в виде корня и наоборот.
, степень с рациональным показателем можно представить в виде корня и наоборот.
Запомните! Степенью числа 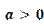 с рациональным показателем
с рациональным показателем  , где m – целое число, а n – натуральное, причём
, где m – целое число, а n – натуральное, причём 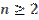 , называется число
, называется число  .
.
Замечание: из определения степени с рациональнымпоказателем сразу следует, что для любого 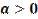 и любого рациональногоr число
и любого рациональногоr число 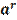 – положительно.
– положительно.
Любое рациональное число допускает различные записи его в виде дроби. По основному свойству дроби частное  можно представить, как частное
можно представить, как частное  , где
, где
n и k – натуральные числа, m – целое число. Тогда при любом a> 0 справедливо равенство 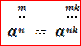 .
.
Заметим, что при отрицательном основании степени рациональная степень числа а не определяется. Отрицательные числа нельзя возводить в рациональную степень, не являющуюся целым числом.
Задание. Найдите значения выражения 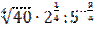 .
.
Решение.
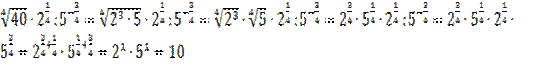
П ри любом действительном 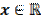 и любом
и любом 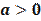
 является положительным действительным числом
является положительным действительным числом 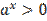 при
при 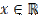 ,
, 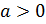 .
.
При таком определении степени с действительным показателем сохраняются все известные вам свойства степени с рациональным показателем. Сформулируем эти свойства.
Пусть 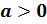 ,
,  ,
, 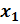 ,
, 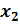 – любые действительные числа. Тогда справедливы следующие равенства.
– любые действительные числа. Тогда справедливы следующие равенства.
Свойства степеней
1. 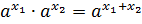 . 2.
. 2. 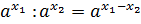 .
.
3. 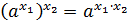 . 4.
. 4. 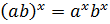 .
.
5. 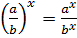 .
.
К этим свойствам добавляется ещё одно:
6. Если 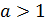 , то
, то 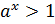 при
при  .
.
ТЕОРЕМА.
Пусть 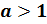 и
и 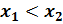 . Тогда
. Тогда 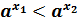 .
.
Из этой теоремы вытекают три следствия.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|