Лекция № 4. ТЕМА ЛЕКЦИИ. Погрешности измерений . Рекомендуемая литература

Лекция № 4

ТЕМА ЛЕКЦИИ

Погрешности измерений

Цель лекции – ознакомить слушателей с классификацией погрешностей измерений, причинами их возникновения, изучить методику оценки погрешностей прямых однократных измерений.

План лекции:

1. Классификация погрешностей измерений

2. Причины возникновения погрешностей измерения

3. Погрешность прямого однократного измерения

Рекомендуемая литература

1. А. Г. Сергеев, М. В. Латышев, В. В. Терегеря. Метрология, стандартизация и сертификация. Стр. 58-68.

2. А. С. Сигов, В. И. Нефедов. Метрология, стандартизация и технические измерения. Стр. 105-106.

Вводная часть

В целях повышения психологического настроя студентов на восприятие данной дисциплины в начале каждой лекции целесообразно проводить короткий опрос по материалу предыдущей лекции.

Вопросы для контроля:

а) Что понимается под средством измерения?

б) Перечислите виды средств измерений.

в) Что понимается под приведенной погрешностью?

Требовать от отвечающих студентов представления перед ответом по форме: «Студент Сергеев. Группа ЭП – 1 – 04». Оценки заносить в журнал преподавателя.

После опроса объявить тему и цель лекции.

Основная часть

1. Классификация погрешностей измерений

При любых видах измерений результат содержит погрешность, связанную с влиянием несовершенства средств измерений, внешних факторов, ошибками наблюдателя и т. д.

Принято различать абсолютную, относительную и приведенную погрешности измерения.

Абсолютная погрешность измерения D

D = X - X_и@ Х - Х_д, (3. 1)

где Х – измеренное значение, т. е. отсчитанное по отсчетному устройству средства измерения; Х_и – истинное значение измеряемой физической величины. В связи с тем, что, как уже отмечалось, истинное значение неизвестно, вместо истинного используется действительное значение физической величины Х_д. Обычно для его определения принимается значение, измеренное наиболее точным измерительным прибором, либо значение, рассчитанное по результатам многократных измерений. Единица измерения абсолютной погрешности совпадает с единицей измерения измеряемой физической величины.

Относительная погрешность измерения

d = (3. 2)

Относительная погрешность, измеряемая в процентах, как наиболее информативная чаще всего используется для характеристики качества измерения. Действительно, по утверждению " напряжение измерено с абсолютной погрешностью ± 1 В" мы не можем судить о качестве (высокое или низкое) проведенного измерения, так как в случае измерения напряжения 10000 В относительная погрешность равна ± 0, 01 %, а при измерении напряжения 10 В относительная погрешность окажется равной ± 10 %, что далеко не равноценно.

Приведенная погрешность измерения

, (3. 3)

где Х_н- нормирующее значение.

В качестве нормирующего значения принимается:

а) конечное значение диапазона измерения для средств измерений с равномерной или степенной шкалой, если нулевая отметка находится на краю или вне шкалы (рис. 2. 1а и 2. 1б);

б) арифметическая сумма конечных значений диапазона измерений, если нулевая отметка находится внутри диапазона (рис. 2. 1в);

в) установленное значение для средств измерений с установленным значением (Х_н= 50 Гц для частотомера с диапазоном измерений 45-50-55 Гц);

г) длина шкалы L для средств измерений с неравномерной шкалой. В этом случае абсолютная погрешность должна выражаться в единицах длины DL.

а) б) в)

Рис. 3. 1. Выбор нормирующего значения Х_н

Приведенная погрешность используется, в частности, для нормирования допускаемой погрешности ряда средств измерений.

При планировании, постановке и проведении измерения либо серии измерений, возникает вопрос о требуемой точности полученного результата. Излишняя точность приводит к неоправданной потере времени и средств. Недостаточная точность зачастую приводит к неверным выводам о пригодности негодного изделия, о зависимости одной величины от другой и т. д. Перед измерением может проводиться априорное оценивание погрешности с целью выбора методики проведения измерения и средств измерения. После проведения измерения может быть проведена апостериорная оценка погрешности.

Точность измерения - качество измерения, отражающее близость их результатов к истинному значению измеряемой величины. Высокая точность соответствует малым погрешностям. Количественно точность выражается через величину, обратную величине относительной погрешности:

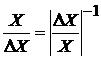где Х – измеренное значение физической величины; DХ = Х - Х_ист - абсолютная погрешность измерения; Х_ист- истинное значение физической величины. Например, если погрешность составляет 0, 01, то точность равна 100.

Известно, что показания электроизмерительного прибора зависят не только от измеряемой величины, но и от изменений значений различных влияющих величин. Влияющая величина - это физическая величина, не измеряемая данным средством измерения, но оказывающая влияние на результаты измерения. Изменение показаний может быть вызвано разнообразными причинами - изменениями температуры окружающего воздуха, давления, влажности, интенсивности и направления электромагнитных полей, угла установки шкалы и т. п.

При проектировании и изготовлении электроизмерительных приборов обычно выделяются основные факторы, влияющие на их показания. В нормативно-технических документах на средства измерений конкретного вида установлены нормальные, рабочие и предельные области значений влияющих величин. Под нормальной областью значений влияющей величины понимается область, в пределах которой изменением результата измерений под ее воздействием можно пренебречь в соответствии с установленными нормами точности. При нормальных условиях определяется основная погрешность средств измерения.

В табл. 3. 1 приведены номинальные значения ряда влияющих величин при нормальных условиях.

Рабочая область - область значений влияющих величин, в пределах которой нормируют дополнительную погрешность или изменение показаний средства измерений. Учесть все влияющие величины практически невозможно,

Таблица 3. 1

Номинальные значения влияющих величин

при нормальных условиях

№ п/п	Влияющая величина	Значение

	Температура для всех видов измерений, ^оС (К)	20 (293)
	Давление окружающего воздуха для измерения ионизирующих излучений, теплофизических, температурных, магнитных, электрических измерений, измерения давления и параметров движения, кПа (мм рт. ст. )	100 (750)
	Давление окружающего воздуха для линейных и угловых измерений, измерения массы, силы света и измерений в других областях, кроме указанных в п. 2, кПа (мм рт. ст. )	101, 3 (760)
	Относительная влажность воздуха для линейных и угловых измерений, измерений массы, измерений в спектроскопии, %
	Относительная влажность воздуха для измерения электрического сопротивления, %
	Относительная влажность воздуха для измерений температуры, силы, твердости, переменного электрического тока, ионизирующих излучений, параметров движения, %
	Относительная влажность воздуха для всех видов измерений, кроме указанных в пп. 4-6, %
	Плотность воздуха, кг× м^-3	1, 2
	Ускорение свободного падения, м/с²	9, 8
	Магнитная индукция (Тл) и напряженность электростатического поля (В/м) для измерений параметров движения, магнитных и электрических величин


	Магнитная индукция и напряженность электростатического поля для всех видов измерений, кроме указанных в п. 10	Соответствует характеристикам поля Земли в данном географическом районе
	Частота питающей сети переменного тока, Гц	50±1%
	Среднеквадратическое значение напряжения питающей сети переменного тока, В	220±10%

так как при выполнении измерений не все численные значения и взаимосвязи с результатом известны. Влияющие величины чаще всего по своей природе являются случайными, следовательно, и результат измерения также является случайной величиной.

Предельные условия измерений - это условия, характеризуемые экстремальными значениями измеряемой и влияющих величин, которые средство измерений может выдержать без разрушений и ухудшения его метрологических характеристик.

Погрешность результата измерения можно рассматривать как сумму составляющих частных погрешностей, каждая из которых обусловлена отклонением влияющего параметра от номинального значения.

Каждая частная погрешность является случайной величиной, так как причины, вызвавшие ее, всегда в большей или меньшей степени случайны. Тем не менее, в общей погрешности измерения, всегда являющейся случайной величиной, можно выделить постоянную неслучайную и случайную величины, которые проявляют себя различно. В соответствии с этим общая погрешность может быть представлена как сумма систематической и случайной составляющих погрешностей. Такое деление является важным с точки зрения применения различных методов анализа и оценке их величин.

2. Причины возникновения погрешностей измерения

Результат измерений имеет ценность только в том случае, если дана оценка погрешности.

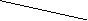∆ X = X - Xu

погрешность результат истинное значение

измерения измерения измеряемой величины

Xu – принципиально неизвестно, так как все реальные приборы имеют какую-то погрешность

Вместо Xu используют Хд – действительное значение измеряемой величины. Оно может быть получено с помощью образцового прибора и настолько приближается к истинному, что для данной цели может быть использовано вместо него:

∆ X = X - Xд

Погрешность измерения имеет ряд составляющих:

1. инструментальная погрешность (погрешность средств измерений)

2. методическая погрешность

3. погрешность оператора

4. погрешность вычислений

Методическая погрешность возникает из-за:

1. не совершенства разработки теории явлений

2. из-за неточности соотношений (вместо сложной формулы используется простая, но менее точная)

3. несоответствие объекта измерений и его модели