
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Классическая теория электропроводности металлов
Электроны проводимости при своем движении сталкиваются с ионами решетки, в результате чего устанавливается термодинамическое равновесие между электронным газом и решеткой. По теории Друде—Лоренца, электроны обладают той же энергией теплового движения, что и молекулы одноатомного газа. Средняя скорость теплового движения электронов
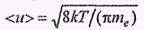
(при Т= 300 К < u> = 1, 1·105 м/с).
При наложении внешнего электрического поля на металлический проводник кроме теплового движения электронов возникает их упорядоченное движение, т. е. возникает электрический ток. Среднюю скорость < 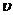 > упорядоченного движения электронов можно оценить по формуле j = ne<
> упорядоченного движения электронов можно оценить по формуле j = ne< 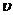 >. При j= 107 А/м2 n = 8-1028 м-3, <
>. При j= 107 А/м2 n = 8-1028 м-3, < 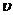 > = 7, 8-10-4 м/с:
> = 7, 8-10-4 м/с:
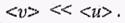
Поэтому при вычислениях результирующую скорость ( 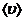 +< u> )можно заменять < u>.
+< u> )можно заменять < u>.
Вывод закона Ома
Со стороны электрического поля (Е = const) в проводнике заряд е испытывает действие силы F= еЕ и приобретает ускорение а =еЕ/m. Скорость электрона к концу свободного пробега 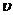 max = eE< t> /m (< t> — среднее время между двумя последовательными соударениями электрона с ионами решетки). Средняя скорость направленного движения электрона
max = eE< t> /m (< t> — среднее время между двумя последовательными соударениями электрона с ионами решетки). Средняя скорость направленного движения электрона
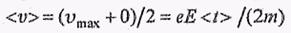
(по теории Друде в конце свободного пробега скорость электрона равна нулю, так как электрон отдает всю энергию ионам решетки).
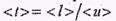
(учтено, что < 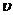 > ˂ ˂ < u>,
> ˂ ˂ < u>,
< /> —средняя длина свободного пробега).
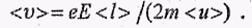
Плотность тока в металлическом проводнике
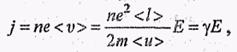
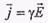 получен закон Ома (сравним с ), где
получен закон Ома (сравним с ), где

Закон Джоуля—Ленца
Дополнительная энергия, приобретаемая электроном к концу свободного пробега,

идет на нагревание металла. Число столкновений электрона за 1с с узлами решетки < z> = < u> /< l> Если n — концентрация электронов, то энергия, передаваемая решетке в единице объема в единицу времени,
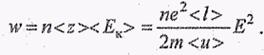
закон Джоуля—Ленца в дифференциальной форме
Закон Видемана—Франца
Отношение теплопроводности к удельной проводимости дня всех металлов при одной и той же температуре одинаково и увеличивается пропорционально температуре:
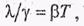
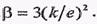 где
где
Классическая теория объяснила законы Ома и Джоуля—Ленца и качественно объяснила закон Видемана—Франца. .
Недостатки классической теории электропроводности
1. Температурная зависимость сопротивления:
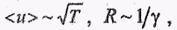
следовательно, 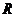 ~
~ 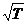 что противоречит опытным данным,, согласно которым R ~ Т,
что противоречит опытным данным,, согласно которым R ~ Т,
2. Экспериментальная оценка среднего пробега электронов также не согласуется с классической теорией Друде—Лоренца,
3. Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла должна быть значительно большей, чем атомная теплоемкость диэлектриков, у которых нет свободных электронов. Однако наличие электронов проводимости практически не сказывается на значении теплоемкости.
Все эти противоречия снимаются квантовой теорией.
Работа выхода электронов из металла.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|