5.2. НАПРЯЖЕНИЯ ПРИ КРУЧЕНИИ

Теория брусьев, имеющих круглое сплошное или кольцевое поперечное сечение, основана на следующих положениях.

Поперечные сечения бруса плоские до деформации остаются плоскими и в деформированном состоянии – гипотеза твердых дисков (Бернулли).

Радиусы поперечных сечений не искривляются и сохраняют свою длину. Поперечные сечения остаются круглыми.

Расстояния между поперечными сечениями вдоль оси бруса не изменяются.

Для установления связи напряжений с внутренними усилиями рассмотрим несколько этапов решения задачи.

Максимальные напряжения при кручении

Из формулы для определения напряжений и эпюры распределения касательных напряжений при кручении видно, что максимальные напряжения возникают на поверхности.

Определим максимальное напряжение, учитывая, что 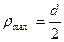, где d — диаметр бруса круглого сечения.

Для круглого сечения полярный момент инерции рассчитывается по формуле.

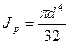Максимальное напряжение возникает на поверхности, поэтому имеем

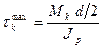Обычно Jp / ρ max обозначают Wp и называют моментом сопротивления при кручении, или полярным моментом сопротивления сечения

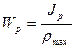Таким образом, для расчета максимального напряжения на поверхности круглого бруса получаем формулу

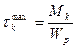Для круглого сечения ; .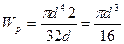

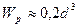Для кольцевого сечения 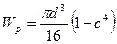, где .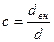

Условие прочности при кручении

Разрушение бруса при кручении происходит с поверхности, при расчете на прочность используют условие прочности

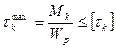где [тк] — допускаемое напряжение кручения.

⇐ Предыдущая 12