ЗАКЛЮЧЕНИЕ

Вывод выражения, определяющего индукцию

магнитного поля в центре кругового постоянного тока,

из выражения, определяющего индукцию магнитного поля

произвольно движущегося точечного электрического заряда

Из потенциалов Лиенара-Вихерта [1] следует, что индукция магнитного поля произвольно движущегося (в том числе, с релятивистской скоростью) точечного электрического заряда определяется строгим выражением:

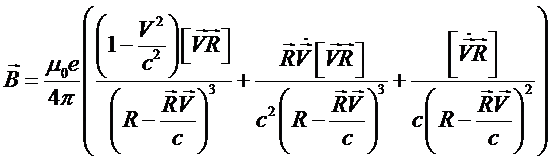(1)

В (1) поле B рассматривается в текущий момент времени t, а скорость заряда V (и ее модуль V), ускорение заряда 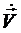, вектор R (и его модуль R) берутся в момент времени t’ = t – R/c. То есть R – вектор, проведенный из точки, в которой находился заряд в момент времени t’ = t – R/c (запаздывающее положение), в точку, в которой определяется поле в текущий момент времени t. μ ₀ – магнитная постоянная. с – скорость света. е – величина заряда.

Используя формулу (1), найдем магнитную индукцию в центре круговой траектории, по которой равномерно (т. е. с постоянной по величине скоростью) движется точечный электрический заряд (рис. 1).

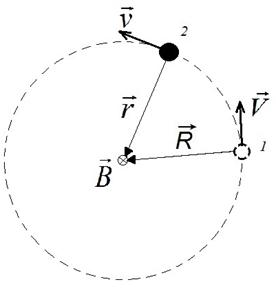
Рисунок 1. Равномерно движущийся по окружности точечный заряд (например, электрон): 2 – положение заряда в рассматриваемый момент времени t; 1 – положение, которое занимал заряд в более ранний момент времени t’ = t – R/c; r=R – радиус окружности; v=V – величина (модуль) скорости заряда.

В этом случае для каждой точки траектории скалярное произведение 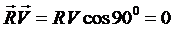(векторы 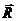и 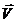ортогональные), векторное произведение 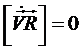(векторы 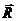и 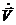коллинеарные). Также 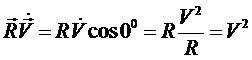(т. к. модуль центростремительного ускорения 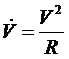[2]). Кроме того, как видно из рисунка 1, .

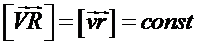Таким образом, выражение (1) принимает вид

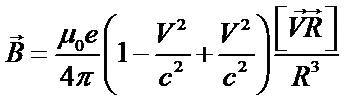
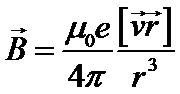(2)

Выражение (2) строго определяет индукцию магнитного поля в центре круговой траектории в случае равномерного движения точечного заряда. Примечательно, что оно имеет такой же вид, как и (в произвольной точке пространства) приближенное “дальнодействующее” выражение для движущегося с нерелятивистской скоростью точечного заряда: запаздывание “квазистационарного” поля компенсируется полем излучения. Здесь, однако, нужно помнить, что (2) выполняется строго для рассматриваемого случая (центра круговой траектории). Для точного определения магнитной индукции в произвольной точке пространства требуется отдельное исследование.

Идентичный вид точной (для центра круговой траектории) формулы (2) и приближенного выражения, определяющего магнитную индукцию движущегося с нерелятивистской скоростью точечного электрического заряда, позволяет далее при выводе выражения, определяющего индукцию магнитного поля в центре кругового постоянного тока, следовать стандартным путём, рассматриваемым, например, в [3]. При этом подразумевается, что постоянный ток протекает по линейному (т. е. тонкому) проводнику.

Рассмотрим круговой постоянный ток (рис. 2). Число электронов dN в элементе d l (т. е. малом отрезке) проводника равно

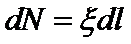, (3)

где ξ - линейная плотность числа электронов в проводнике (т. е. число электронов на единицу длины проводника), dl – длина элемента проводника. Нужно помнить, что ξ из-за лоренцева сокращения является функцией скорости электронного потока.

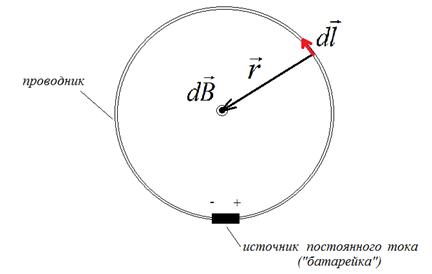
Рисунок 2. Электрическая цепь, по которой протекает круговой постоянный ток. Подразумевается, что материал проводника обладает достаточно высоким удельным сопротивлением (либо в разрыв цепи включена нагрузка), и, тем самым, источник тока не работает в режиме короткого замыкания. Однако нужно помнить, что магнитное поле (неподвижной) цепи с постоянным током определяется только ее геометрией и силой протекающего в ней тока и не зависит от режима работы источника тока.

Электроны, принадлежащие в данный момент времени рассматриваемому элементу проводника d l , создают в центре кругового постоянного тока (рис. 2) магнитное поле

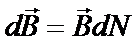, (4)

где 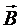- индукция магнитного поля, создаваемого одним электроном в центре кругового тока (см. (2)).

Подставим (2) и (3) в (4) с учетом, что для электронов 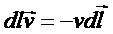(направление движения электронов исторически принято противоположным направлению тока):

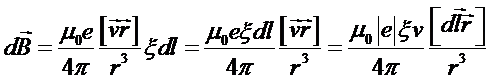, (5)

где 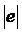- абсолютная величина (модуль) заряда электрона.

Принимая во внимание, что сила тока равна 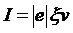[3], запишем (5) в виде

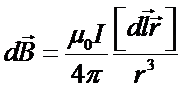, (6)

Индукцию магнитного поля 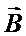в центре кругового постоянного тока найдем интегрированием (6) по всем элементам :

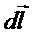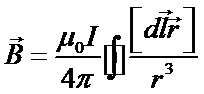, (7)

Так как вклады 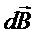в суммарное магнитное поле 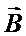в центре кругового постоянного тока от всех элементов 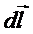коллинеарные, величина магнитной индукции B здесь вычисляется сложением величин вкладов dB:

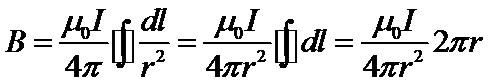, (8)

где учтено, что r=const – радиус кругового тока, 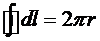– длина кругового тока, векторы 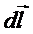и 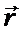взаимно перпендикулярные, и, следовательно, величина их векторного произведения .

Окончательно (8) принимает вид

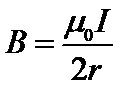. (9)

Выражение (9) определяет величину (модуль) индукции магнитного поля в центре кругового постоянного тока. На практике оно применимо к круговому постоянному току, радиус r которого значительно превосходит поперечные размеры проводника; также предполагается, что цепь не содержит ферромагнетиков и находится в вакууме или среде, магнитными свойствами которой можно пренебречь (воздух и т. п. ).

Формула (9), полученная из строгого релятивистского выражения (1), совпадает с результатом, полученным из приближенного нерелятивистского выражения индукции магнитного поля движущегося заряда (см. [3]).

ЗАКЛЮЧЕНИЕ

В электродинамике справедливость интеграла (7) для линейной цепи произвольной геометрической конфигурации с постоянным током во всем пространстве строго доказывается путем решения (с помощью введения в рассмотрение векторного потенциала) одного из уравнений Максвелла 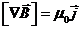, справедливого для стационарных токов (см. [1]).

Здесь же, исходя из выражения (1), показана строгая справедливость интеграла (7) только для центра кругового линейного постоянного тока. Доказательство справедливости интеграла (7), исходя из (1), во всемпространстве для кругового линейного постоянного тока, очевидно, представляет немалые математические трудности. В еще большей степени это относится к току произвольной геометрической конфигурации.

ЛИТЕРАТУРА

1. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб. пособие. В 10 т. Т. II. Теория поля. — 7-е изд., испр. — М.: Наука. Гл. ред. физ. -мат. лит., 1988. — 512 с.

2. Савельев И. В. Курс общей физики: Учеб. пособие. В 3-х т.

Т. 1. Механика. Молекулярная физика. — 3-е изд., испр. — М.: Наука. Гл. ред. физ. -мат. лит., 1987. — 432 с., ил.

3. Савельев И. В. Курс общей физики: Учеб. пособие. В 3-х т.

Т. 2. Электричество и магнетизм. Волны. Оптика. — 3-е изд., испр. — М.: Наука. Гл. ред. физ. -мат. лит., 1988. — 496 с., ил.