Практическая работа. Тема «Построение графиков показательной и логарифмической функций различными преобразованиями». Общие виды преобразования графика функции y= f(x)

Практическая работа

Тема «Построение графиков показательной и логарифмической функций различными преобразованиями»

Цель: изучить способы построения графиков показательной и логарифмической функций.

План лекции:

1. Способы построения графиков показательной и логарифмической функций

2. Общие виды преобразования графика вида y = f(x).

Построим график показательной функции f(х) = 2^х.

Для этого составим таблицу и построим точки в системе координат, затем соединяем плавной линией, получаем график функции.

х						- 1	- 2	- 3
у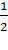

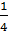
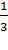
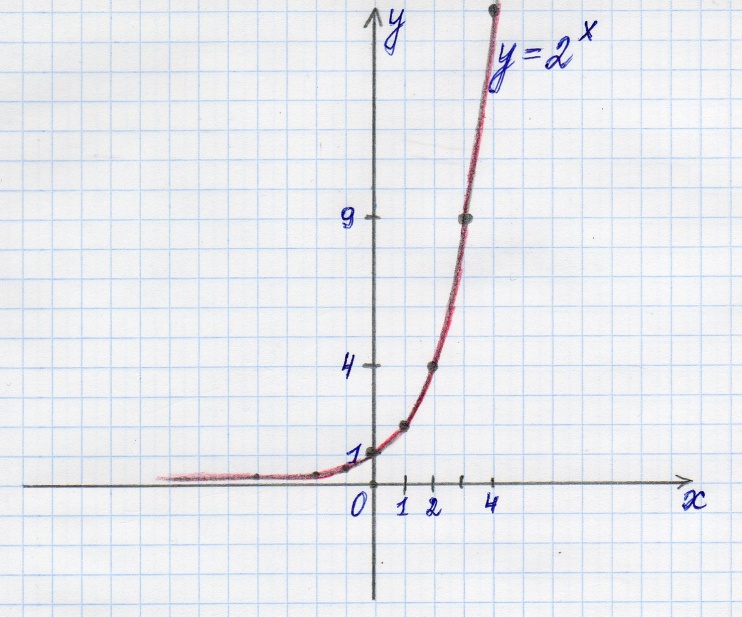
Чтобы построить график логарифмической функции у = 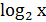то же можно действовать аналогичным способом.

Можно использовать и другой способ, основанный на том, что функция

у = 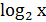является обратной к показательной функции f(х) = 2^х.

Графики этих функций симметричны относительно прямой у = х.

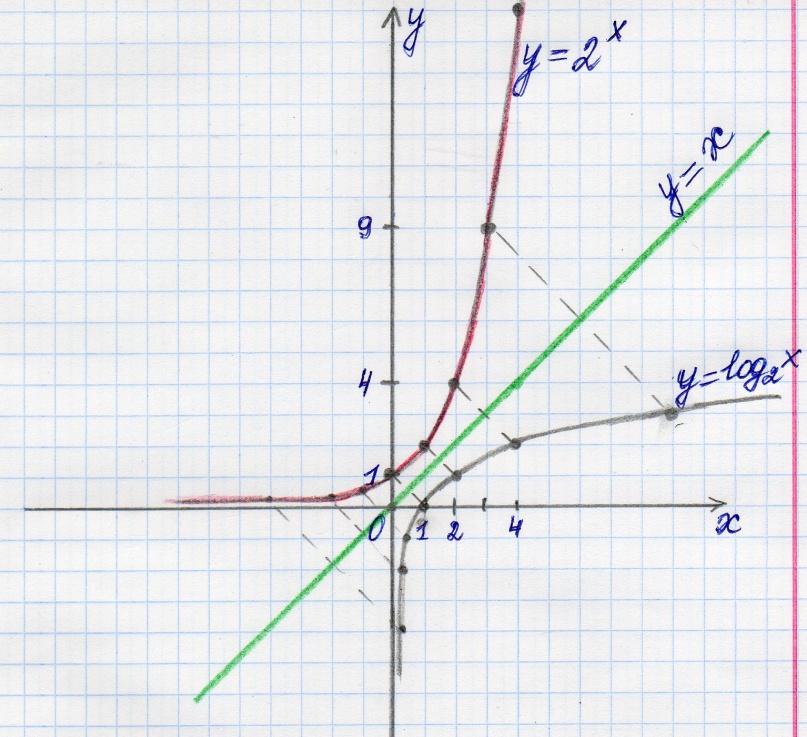
Чтобы построить график показательной функции f(х) = 2^-х, достаточно симметрично отобразить график функции f(х) = 2^хотносительно оси Оу.

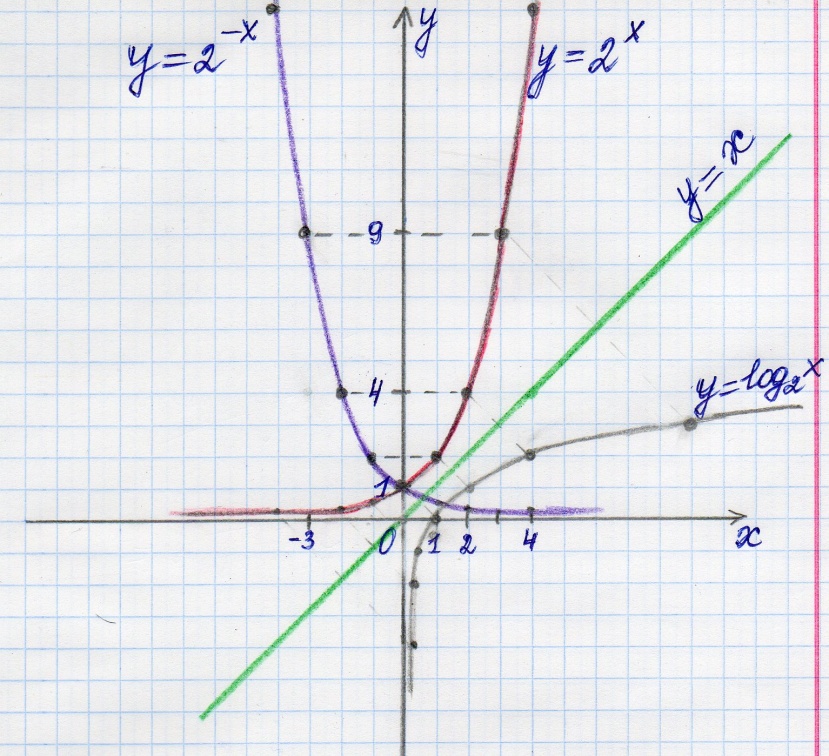
Существует ряд общих видов преобразований графиков функций, т. е. построения графиков более сложных показательных и логарифмических функций, основываясь на более простых.

Например, построения графика функции f(х) = 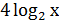+ 1, основываясь на графике функции f(х) = 2^х или у = .

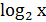Общие виды преобразования графика функции y= f(x)

А.	Для построения графика функции y= f(x) + b, где b - постоянное число, надо перенести график f на вектор (0; b) вдоль оси ординат Оу.
Б.	Для построения графика функции y = k· f(x) + b, где b - постоянное число, надо растянуть график функции y = f (x) в k раз вдоль оси ординат Оу.
В.	График функции y= f(x + к) получается из графика f переносом вдоль оси абсцисс Ох на вектор (к; 0) вправо.
Г.	График функции y= f(x - к) получается из графика f переносом вдоль оси абсцисс Ох на вектор (к; 0) влево.

Примеры.

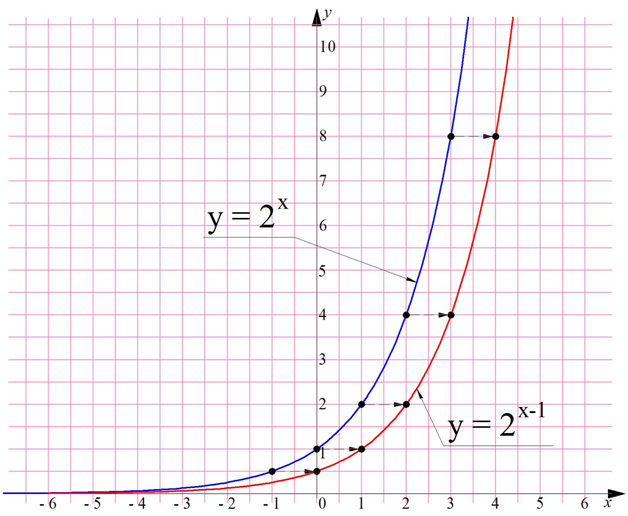
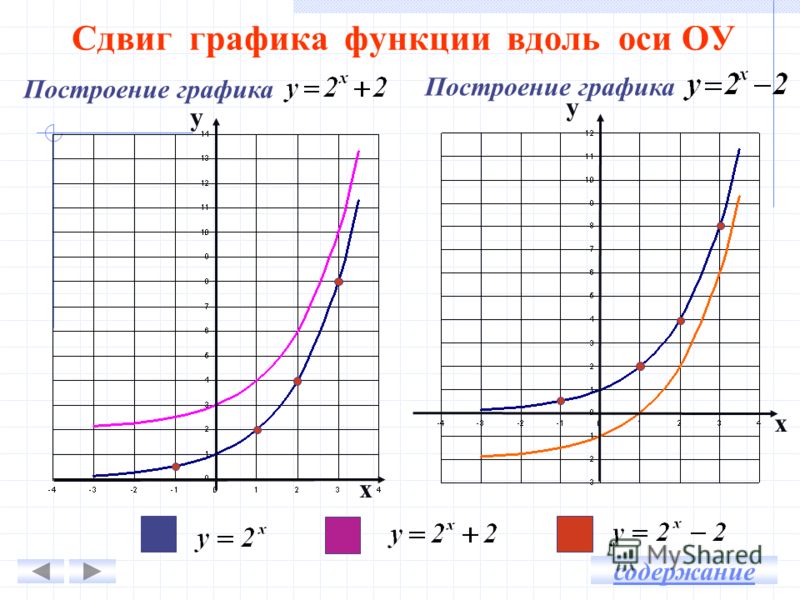
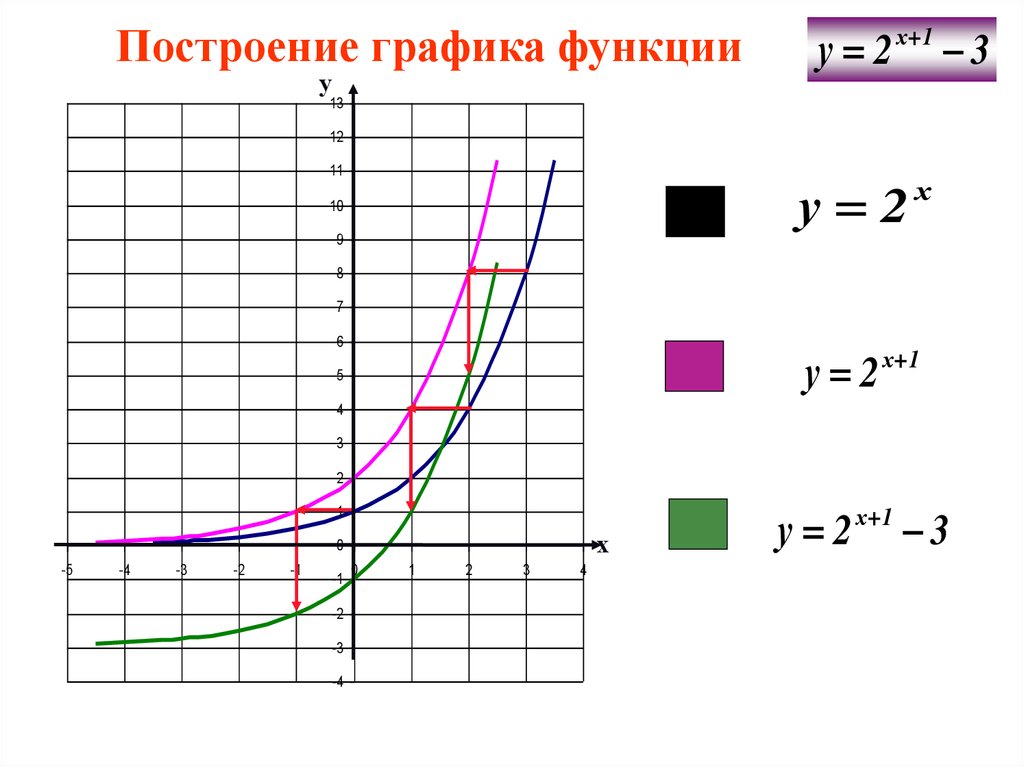
Контрольные вопросы:

1. Что можно сказать о графиках показательной и логарифмической функций, имеющих одинаковое основание, относительно прямой y = x?

2. Какие общие виды преобразования графика функции y = f(x) вы знаете? Приведите примеры на каждое преобразование.

3. Постройте график функции:

а) у = х^-3; в) у = 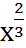; д) у = ;

б) у = х^-4; г) у = 2^х; е) у = .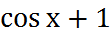

4. На основе графика у = 3^х постройте графики функций

у = 3^х – 2, у = 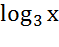+ 1, у = 2· 3^х+1.