
- Р Р‡.МессенРТвЂВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВнокласснРСвЂВВВВВВРєРСвЂВВВВВВ
- Telegram
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВРЎР‚
- LiveJournal
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
УРАВНЕНИЯ И НЕРАВЕНСТВА
З а д а н и е 1. Решите уравнение:
1) 3х = 0; 2) –4х = –8; 3) 6х = – 12;
х = 0. х = 2. х =
4) х + 2 = 4 – х; 5) 2х – 7 = 9; (Д/З) 6) (2х + 3) – (4х – 1) = 4;
х + х = 4 – 2; 2х + 3 – 4х + 1 = 4;
2х = 2; 2х – 4х = 4 – 3 – 1;
х = 1. – 2х = 0;
х = 0.
| 3х – 4 = 5 – 2х + 1; 3х + 2х = 5 + 1 + 4; 5х = 10; х = 2. |
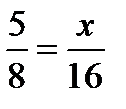 ; 10) 8: х = 2: 5 (Д/З)
; 10) 8: х = 2: 5 (Д/З)
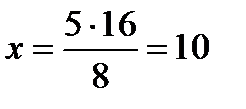 .
.
11) 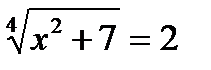 ; 12)
; 12) 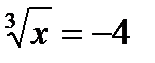 ; (Д/З)
; (Д/З)
х2 + 7 = 24;
х2 + 7 = 16;
х2 = 16 – 7;
х2 = 9;
х = ± 3.
13)  ; 14)
; 14) 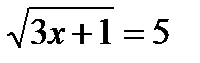 ; (Д/З)
; (Д/З)
х – 7 = 42;
х – 7 = 16;
х = 23.
15)  ; 16)
; 16) 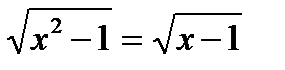 ; (Д/З)
; (Д/З)
х = х2 – 2;
х2 – х – 2 = 0;
по теореме Виета 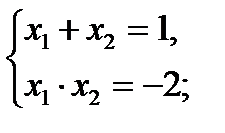
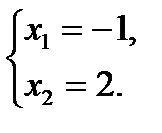
Проверка.
При х = – 1 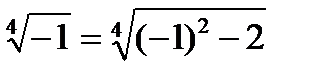 ;
;  ― не верно, то х = – 1 ― посторонний корень.
― не верно, то х = – 1 ― посторонний корень.
При х = 2 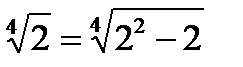 ;
; 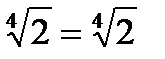 ― верно, то х = 2 ― корень уравнения.
― верно, то х = 2 ― корень уравнения.
Ответ: 2.
17) 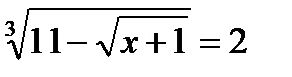 ; 18)
; 18) 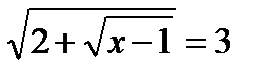 ; (Д/З)
; (Д/З)
11 – 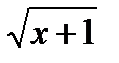 = 23;
= 23;
11 –  = 8;
= 8;
–  = 8 – 11;
= 8 – 11;
–  = – 3; | × (–1)
= – 3; | × (–1)
 = 3;
= 3;
х + 1 = 32;
х + 1 = 9;
х = 8.
Проверка.
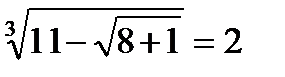 ;
; 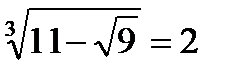 ;
; 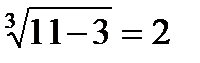 ;
; 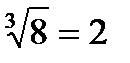 ; 2 = 2 ― верно.
; 2 = 2 ― верно.
Ответ: 8.
19) 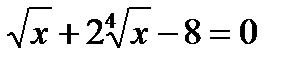 ; 20)
; 20) 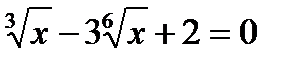 ; (Д/З)
; (Д/З)
при замене  , то
, то  и получим:
и получим:
у2 + 2у – 8 = 0;
по теореме Виета 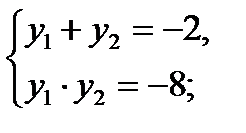
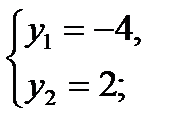
решим два уравнения:
1.  ; 2.
; 2.  ;
;
нет корней, т. к. – 4 < 0; х = 24;
х = 16.
Ответ: 16.
21) 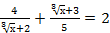 ; 22)
; 22) 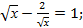 (Д/З)
(Д/З)
при замене 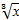 = у получим: 23)
= у получим: 23) 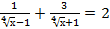 ; (Д/З)
; (Д/З)
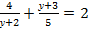 ; 24)
; 24)  ; (Д/З)
; (Д/З)
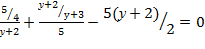 ; при замене
; при замене 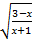 = у, то
= у, то 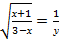 и получим:
и получим:
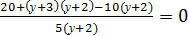 ;
; 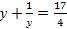 ;
;
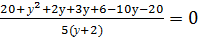 ; …Дорешать самостоятельно
; …Дорешать самостоятельно
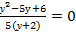 ;
;
у2 – 5у + 6 = 0; 5(у +2) ≠ 0;
| у ≠ – 2; |
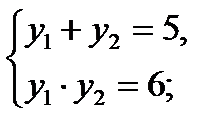

решим два уравнения:
1. 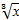 = 2; 2.
= 2; 2. 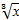 = 3;
= 3;
х = 8; х = 27.
Ответ: 8; 27.
25) 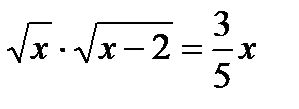 ; 26)
; 26) 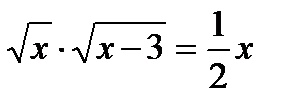 ; (Д/З)
; (Д/З)
5 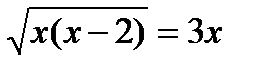 ;
;
25х(х – 2) = (3х)2;
25х2 – 50х = 9х2;
25х2 – 50х – 9х2= 0;
16х2 – 50х = 0;
2х(8х – 25) = 0;
2х = 0 или 8х – 25 = 0;
х = 0 8х = 25;
х = 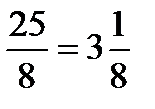 .
.
Проверка.
При х = 0 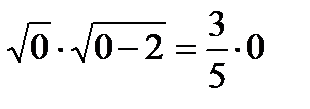 ;
; 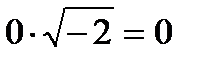 ― не верно, то х = 0 ― посторонний корень.
― не верно, то х = 0 ― посторонний корень.
При х = 
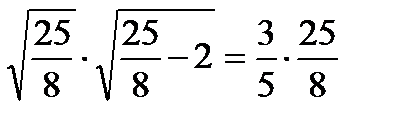 ;
; 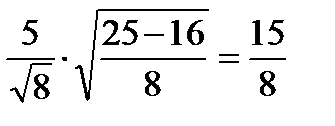 ;
; 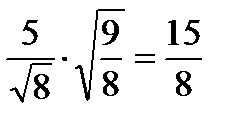 ;
;
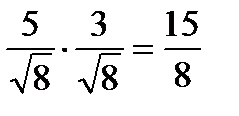 ;
; 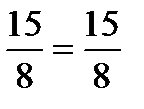 ― верно, то х =
― верно, то х = 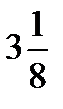 ― корень уравнения.
― корень уравнения.
Ответ:  .
.
27) 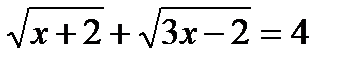 ; 28)
; 28) 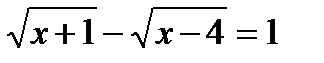 ; (Д/З)
; (Д/З)
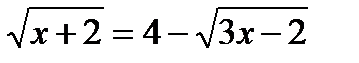 ;
;
х + 2 = (4 – 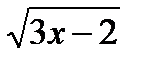 )2;
)2;
х + 2 = 16 – 8  + 3х – 2;
+ 3х – 2;
8  = 16 + 3х – 2 – х – 2;
= 16 + 3х – 2 – х – 2;
8  = 2х + 12; |: 2
= 2х + 12; |: 2
4  = х + 6;
= х + 6;
16(3х – 2) = (х + 6)2;
48х – 32 = х2 + 12х + 36;
х2 + 12х + 36 – 48х + 32 = 0;
х2 – 36х + 68 = 0;
по теореме Виета 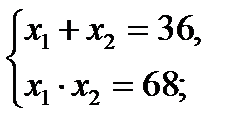
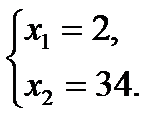
Проверка.
При х = 2  ; 4 = 4 ― верно, то х = 2 ― корень уравнения.
; 4 = 4 ― верно, то х = 2 ― корень уравнения.
При х = 34 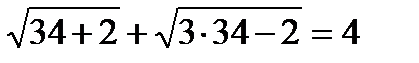 ; 16 = 4 ― не верно, то х = 34 ― посторонний корень.
; 16 = 4 ― не верно, то х = 34 ― посторонний корень.
Ответ: 2.
29) 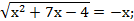 30)
30) 
31) 2х – 1 = 32; 32) 54 – х= 125; (Д/З) 33) 0, 4х= 0, 064; 34) 0, 6х= 0, 36; (Д/З)
2х – 1 = 25; 0, 4х= 0, 43;
х – 1 = 5; х = 3.
х = 6.
35) 3х = 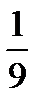 ; 36)
; 36) 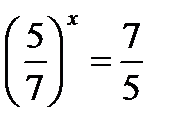 ; (Д/З) 37)
; (Д/З) 37) 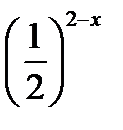 = 23х; 38) 4х – 2 =
= 23х; 38) 4х – 2 = 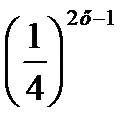 ; (Д/З)
; (Д/З)
3х = 3–2; 2х – 2 = 23х;
х = –2. х – 2 = 3х;
– 2х = 2;
х = – 1.
| 23х · 22х = 210; 25х= 210; 5х = 10; х = 2. |

2–3х = 22х +1;
…
82 · 8х– 8х = 126; 47) 3х+3+ 5 · 3х – 1 = 86;
8х · (82 – 1) = 126;
63 · 8х = 126 |: 63;
23х = 21;
8х = 2;
3х = 1;
х = 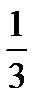 . .
|
 ; 44)
; 44) 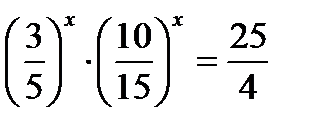 ; (Д/З) 45) 8х + 2– 8х = 126; 46) 22х+3+ 4х = 72; (Д/З)
; (Д/З) 45) 8х + 2– 8х = 126; 46) 22х+3+ 4х = 72; (Д/З)
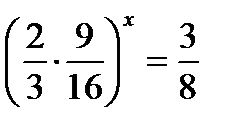 ;
;
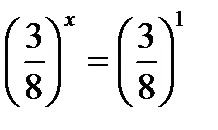 ;
;
х = 1.
4х + 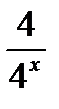 = 5;
при замене 4х = у получим:
у + = 5;
при замене 4х = у получим:
у + 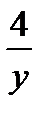 = 5;
…Дорешать самостоятельно = 5;
…Дорешать самостоятельно
|
32х– 2 · 31 · 3х – 27 = 0;
32х– 6 · 3х – 27 = 0;
при замене 3х = у получим:
у2– 6у – 27 = 0;
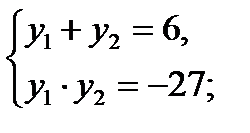
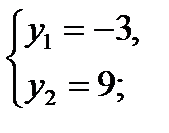
решим два уравнения:
1. 3х = –3; 2. 3х = 9;
нет корней, т. к. –3 < 0; 3х = 32;
х = 2.
Ответ: 2.
51) 6 · 4х – 13 · 6х + 6 · 9х = 0; 52) 4 · 32х + 3х · 4х – 3 · 42х = 0; (Д/З)
6 · 22х – 13 · 2х · 3х + 6 · 32х = 0;
разделим уравнение на 32х ≠ 0 и получим:
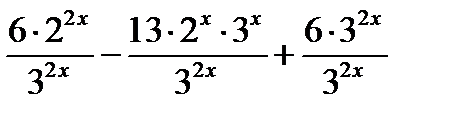 = 0;
= 0;
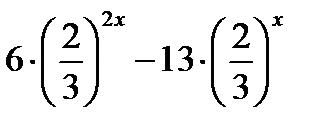 + 6 = 0;
+ 6 = 0;
при замене 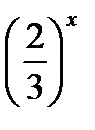 = у получим:
= у получим:
6у2– 13у + 6 = 0;
D = (–13)2 – 4 · 6 · 6 = 169 – 144 = 25 = 52;
у1 = 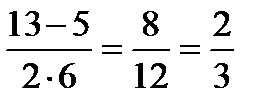 ; у2 =
; у2 = 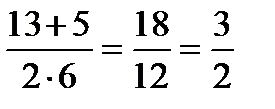 ;
;
решим два уравнения:
1. 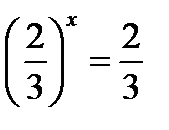 ; 2.
; 2. 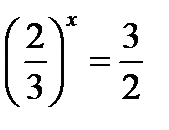 ;
;
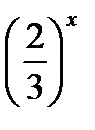 =
= 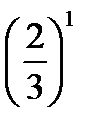 ;
; 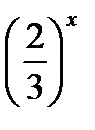 =
=  ;
;
х = 1; х = –1.
Ответ: –1 и 1.
| х2 – 3 = 13; х2=16; х = ±4. |
| х = 32; х = 9. |
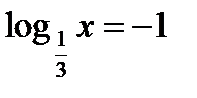 ; 55) log12(х2 – 3) =log1213;
; 55) log12(х2 – 3) =log1213;
х = 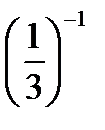 ;
;
х = 3.
56) log6 x = – 2; (Д/З)57)log0, 4х = 3; (Д/З) 58) log2(х2 + 5) =log254; (Д/З)
log4x = log4 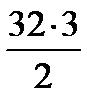 ;
log4x = log448;
х = 48. ;
log4x = log448;
х = 48.
|
| 4x+ 1 = 7 – 2x; 4х + 2х = 7 – 1; 6х = 6; х = 1. Проверка. log2 (4 · 1+ 1) = log2 (7 – 2 · 1); log2 5 = log2 5 ― верно. Ответ: 1. |
log 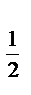 (3x – 2) = – 2;
(3x – 2) = – 2;
3х – 2 = 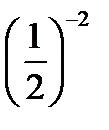 ;
;
3х – 2 = 4;
3х = 6;
х = 2.
62) log0, 2 (2x – 3) = – 1; 63) log7x = log7 2, 5 + 4log7 2 − log710; 64)log5 (x + 4) = log5 (1 – 2x); (Д/З)
65) 2log5 (x+ 2) = log5 (2x+ 12); 66) 2log3 (x – 1) = log3 (4x + 1); (Д/З)
log5 (x + 2)2 = log5 (2x + 12);
(x + 2)2 = 2x + 12;
х2 + 4х + 4 – 2х – 12 = 0;
х2 + 2х – 8 = 0;
по теореме Виета 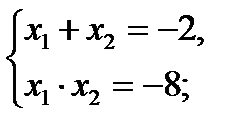
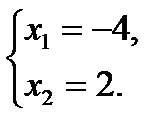
Проверка.
При х = –4 2log5 (–4 + 2) = log5 (2 · (–4) + 12); 2log5 (–2) = log54 ― не верно, то
х = –4 ― посторонний корень.
При х = 2 2log5 (2 + 2) = log5 (2 · 2 + 12); 2log5 4 = log5 16; log5 16 = log5 16― верно, то
х = 2 ― корень уравнения.
Ответ: 2.
67) 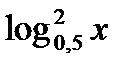 + log0, 5 x – 6 = 0; 68) log6(x – 2) + log6(x – 11) = 2;
+ log0, 5 x – 6 = 0; 68) log6(x – 2) + log6(x – 11) = 2;
при замене log0, 5 x = у получим: log6(x – 2)(x – 11) = 2;
у2+ у – 6 = 0; (x – 2)(x – 11) = 62;
х2 – 11х – 2х + 22 – 36 = 0;
х2 – 13х – 14 = 0;
по теореме Виета 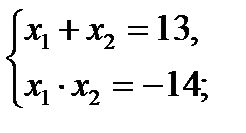 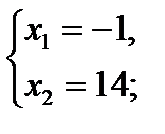 Проверка.
При х = –1 log6(–1 – 2) + log6(–1 – 11) = 2;
log6(–3) + log6(–12) = 2 ― не верно, то
х = –1 ― посторонний корень.
При х = 14 log6(14 – 2) + log6(14 – 11) = 2;
log612 + log63 = 2; log636 = 2; 2 = 2― верно,
тох = 14 ― корень уравнения.
Ответ: 14.
Проверка.
При х = –1 log6(–1 – 2) + log6(–1 – 11) = 2;
log6(–3) + log6(–12) = 2 ― не верно, то
х = –1 ― посторонний корень.
При х = 14 log6(14 – 2) + log6(14 – 11) = 2;
log612 + log63 = 2; log636 = 2; 2 = 2― верно,
тох = 14 ― корень уравнения.
Ответ: 14.
|
решим два уравнения:
1. log0, 5 x = –3; 2. log0, 5 x = 2;
х = 0, 5–3 = 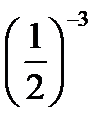 ; х = 0, 52;
х = 8; х = 0, 25. Ответ: 8 и 0, 25. ; х = 0, 52;
х = 8; х = 0, 25. Ответ: 8 и 0, 25.
|
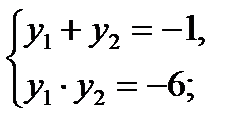
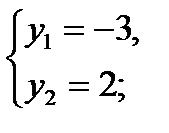
69) 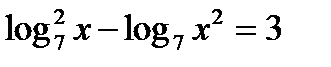 ; (Д/З)70) log2 (2x – 1) = 2log 2 3 – log2 (x – 4); (Д/З)
; (Д/З)70) log2 (2x – 1) = 2log 2 3 – log2 (x – 4); (Д/З)
71) 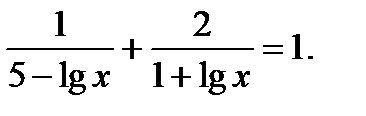 (Д/З)
(Д/З)
З а д а н и е 2. Решите неравенство:
1) –2х ≥ – 6; 2) 4х> 20; 3) –3х ≤ 12; (Д/З)
х ≤ 3; х> 5; 4) 6х< –18; (Д/З)
///////////////• х ο ///////////// х
– ∞ 3 5 +∞
х 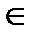 (– ∞; 3]. х
(– ∞; 3]. х 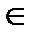 (5; +∞ ).
(5; +∞ ).
5) х + 3 > 2х – 7; 6) х2 + х≥ 0; 7) х2 + х – 2 < 0;
х – 2х> –7 – 3; х2 + х = 0; х2 + х – 2 = 0;
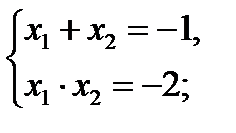 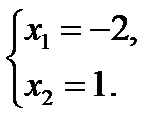
|
х< 10; х = 0 или х + 1 = 0;
///////////////ο хх = –1;
– ∞ 10 + – +
х 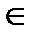 (– ∞; 10). ////////////• •//////////// х + – +
(– ∞; 10). ////////////• •//////////// х + – +
– ∞ –1 0 +∞ ο //////////ο х
х 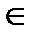 (– ∞; –1]U [0; +∞ ). –2 1
(– ∞; –1]U [0; +∞ ). –2 1
х 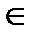 (– 2; 1)
(– 2; 1)
8) 6 – 2х ≤ 4; (Д/З) 9) х2 – 2х ≤ 0; (Д/З) 10) х2 – 3х– 4 ≥ 0; (Д/З)
11) 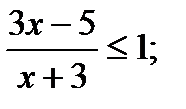 (Найти сумму целых решений) 12)
(Найти сумму целых решений) 12) 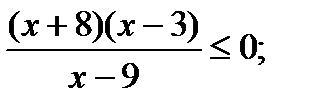 (Д/З)
(Д/З)
 13)
13) 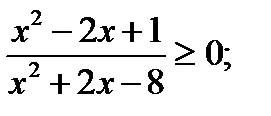 (Д/З)
(Д/З)
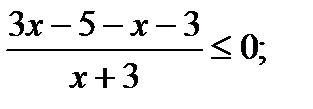
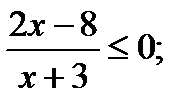
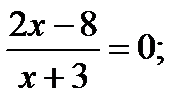
2х – 8 = 0; х + 3 ≠ 0;
2х = 8; х ≠ – 3;
х = 4.
+ – +
ο //////////•х
–34
х  (– 3; 4].
(– 3; 4].
Сумма целых решений – 2 + (– 1) + 0 + 1 + 2 + 3 + 4 = 7.
Ответ: 7.
Правила: 1. Если в показательном неравенстве основаниеа> 1, то для показателей степени знак неравенства сохраняется.
2. Если в показательном неравенстве основание 0< а< 1, то для показателей степени знак неравенства меняется.
14) 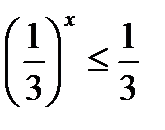 ; 15)
; 15) 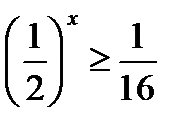 ; (Д/З)
; (Д/З)
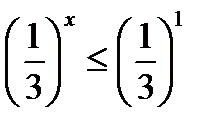 ;
;
т. к. основание 0 < 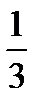 < 1, то для показателей степени знак неравенства меняется:
< 1, то для показателей степени знак неравенства меняется:
х ≥ 1.
•///////////// х
1 +∞
х 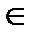 [1; +∞ ).
[1; +∞ ).
16) 32х + 9< 27; 17) 53х– 4 > 25; (Д/З)
32х + 9< 33;
т. к. основание 3 > 1, то для показателей степени знак неравенства сохраняется:
2х + 9 < 3;
2х< – 6;
х< – 3.
///////////////ο х
– ∞ – 3
х 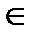 (– ∞; – 3).
(– ∞; – 3).
18) 0, 25 – х≤ 0, 008; 19) 0, 7х+1< 0, 49; (Д/З)
0, 25 –х≤ 0, 23;
т. к. основание 0 < 0, 2 < 1, тодля показателей степени знак неравенства меняется:
5 – х≥ 3;
– х≥ –2;
х≤ 2.
///////////////• хх 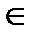 (– ∞; 2].
(– ∞; 2].
– ∞ 2
20) 6х+4> 1; 21) 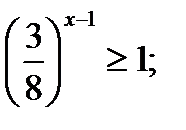 (Д/З)
(Д/З)
6х+4> 60;
т. к. основание 6 > 1, то для показателей степени знак неравенства сохраняется:
х + 4 > 0;
х> –4.
o///////////// х
–4 +∞
х  (–4; +∞ ).
(–4; +∞ ).
22) 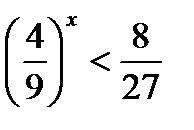 ; 23) 4х ≤ 32; (Д/З)
; 23) 4х ≤ 32; (Д/З)
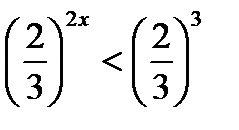 ;
;
т. к. основание 0 < 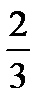 < 1, то для показателей степени знак неравенства меняется:
< 1, то для показателей степени знак неравенства меняется:
2х> 3;
х> 1, 5.
o///////////// х
1, 5 +∞
х  (1, 5; +∞ ).
(1, 5; +∞ ).
32х– 12 · 3х + 27 ≥ 0;
при замене 3х = у получим:
у2– 12у + 27 ≥ 0;
у2– 12у + 27 = 0;
по теореме Виета 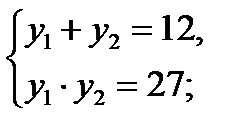 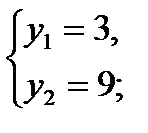
|
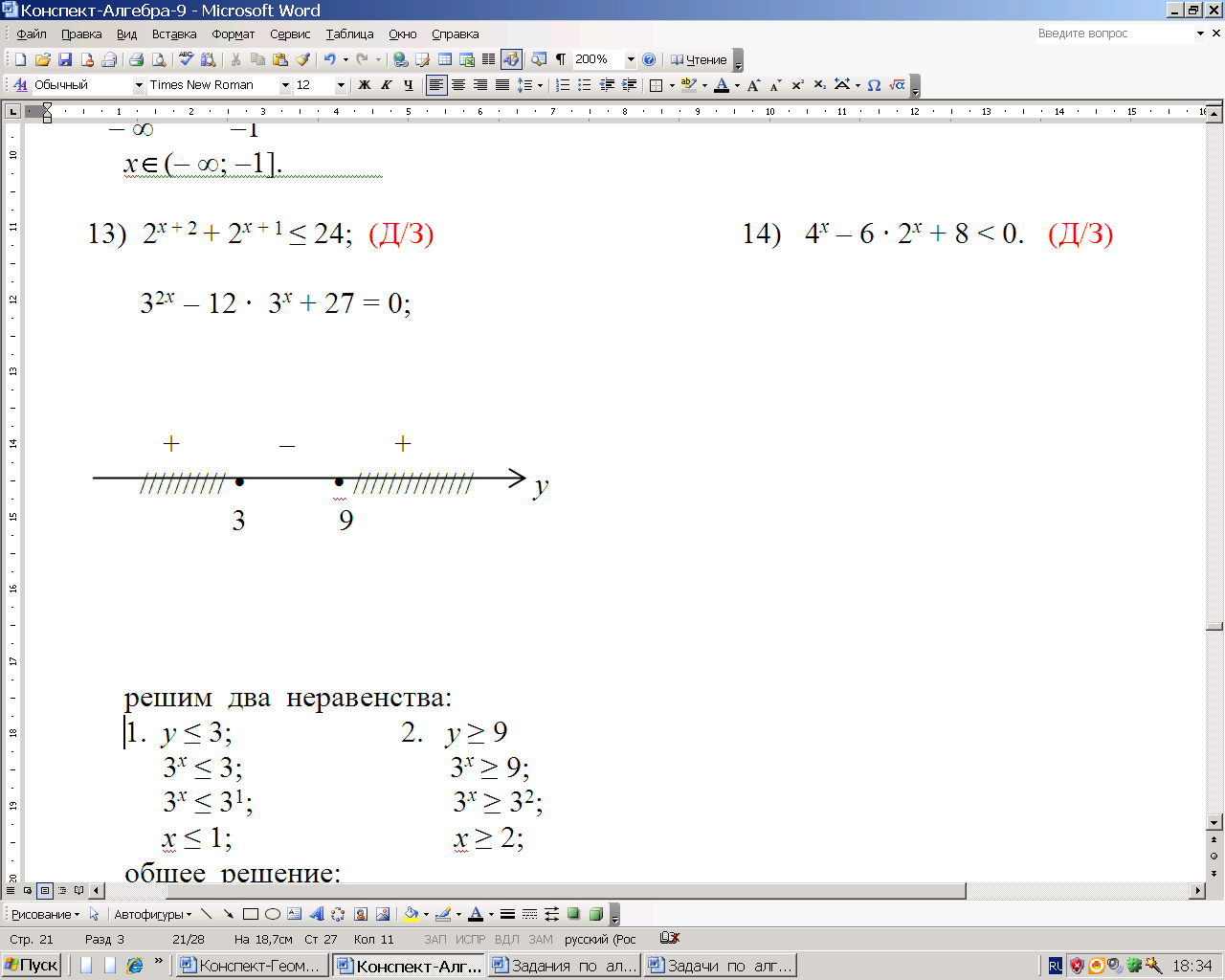
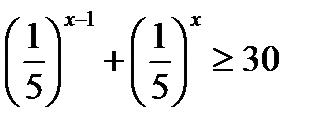 ; 25) 9х– 12 · 3х + 27 ≥ 0;
; 25) 9х– 12 · 3х + 27 ≥ 0;
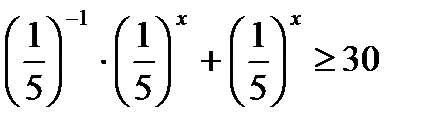 ;
;
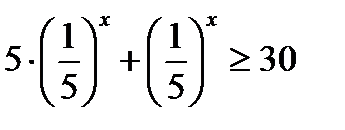 ;
;
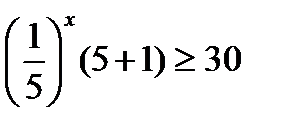 ;
;
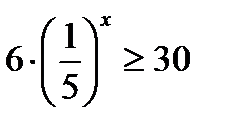 |: 6;
|: 6;
| решим два неравенства: 1. у ≤ 3; 2. у ≥ 9; 3х ≤ 3; 3х ≥ 9; 3х ≤ 31; 3х ≥ 32; х ≤ 1; х ≥ 2; общее решение: |
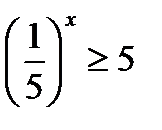 ;
;
 ;
;
 х ≤ –1.
х ≤ –1.
///////////////• х
– ∞ –1
х  (– ∞; –1].
(– ∞; –1].
26) 2х + 2 + 2х + 1 ≤ 24; (Д/З)27) 4х – 6 ∙ 2х + 8 < 0. (Д/З)
Правила: 3. Если в логарифмическом неравенстве основаниеа> 1, то для выражений под логарифмом знак неравенства сохраняется.
4. Если в логарифмическом неравенстве основание 0< а< 1, то для выражений под логарифмом знак неравенства меняется.
28) 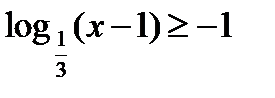 ; 29) lg (x+2) > 3;
; 29) lg (x+2) > 3;
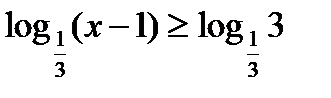 , т. к.
, т. к. 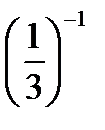 = 3; lg (x + 2) > lg 1000, т. к. 103 = 1000;
= 3; lg (x + 2) > lg 1000, т. к. 103 = 1000;
т. к. основание 0 < 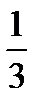 < 1, то для выражений т. к. основание 10 > 1, то для выражений под
< 1, то для выражений т. к. основание 10 > 1, то для выражений под
под логарифмом знак неравенства меняется: логарифмом знак неравенства сохраняется:
0 < х – 1 ≤ 3; х + 2 > 1000;
1 < х ≤ 4; х> 998;
ο //////////•хo///////////// х
1 4 998 +∞
х  (1; 4]. х
(1; 4]. х 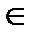 (998; +∞ ).
(998; +∞ ).
30) log0, 8 (x + 6) < log0, 8 9; (Д/З) 31) log3 (x + 3) < log3 4; (Д/З)
32) 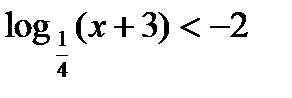 ; (Д/З)33)
; (Д/З)33) 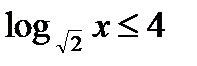 ; (Д/З)
; (Д/З)
34) log3(4x – 5)< log37 + 2; 35) log0, 7(x + 4)> log0, 7(19 – 4x);
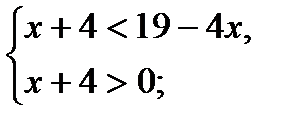 
|
log3(4x – 5)< log37 + log39;
log3(4x – 5)< log363;
т. к. основание 3> 1, то для выражений под
логарифмом знак неравенства сохраняется: – 4 3
0 < 4х – 5 < 63; //////////////ο //////////ο х
5 < 4х< 68; \\\\\\\\\\\\\\\\\\\\\\\\\\
1, 25 < х< 17; х 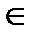 (– 4; 3).
(– 4; 3).
ο //////////ο х
1, 2517
х 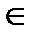 (1, 25; 17).
(1, 25; 17).
36) log2(3x + 2)< log25 + 4; (Д/З)37)log7(4x – 6)> log7(2x – 4); (Д/З)
38) 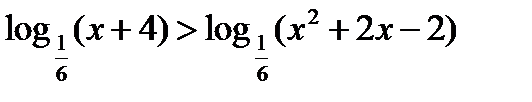 ; 39)
; 39) 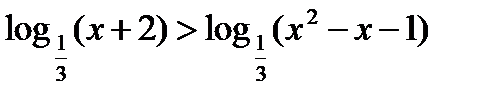 ; (Д/З)
; (Д/З)
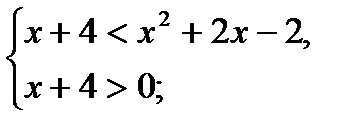
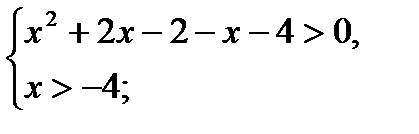

x2 + x – 6 > 0;
x2 + x – 6 = 0;
по теореме Виета 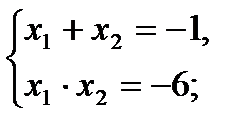
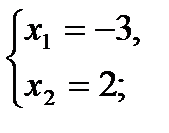
+ – +
////////////////ο ο //////////// х
–32
общее решение:
– 4– 32
/////////////////ο ////////////ο ο //////////////// х
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
х  (– 4; – 3) U(2; + ∞ ).
(– 4; – 3) U(2; + ∞ ).
40) log 6 (x + 1) + log 6 (2x + 1) ≤ 1; 41) log 4 (x + 3) + log 4 (x + 15) ≥ 3. (Д/З)
log6 (x + 1)(2x + 1) ≤ log 66;
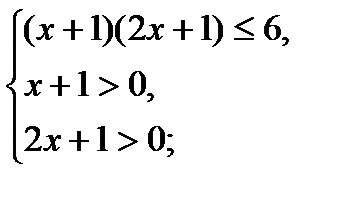
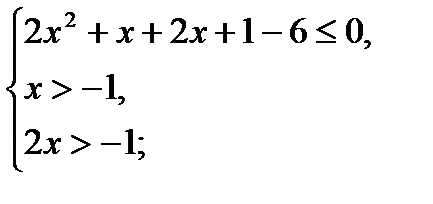
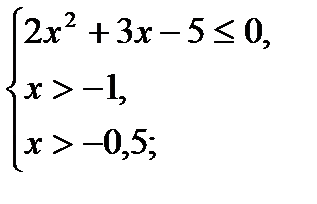
2x2 + 3x – 5 ≤ 0;
2x2 + 3x – 5 = 0;
D = 32 – 4 · 2 · (– 5) = 49 = 72;
х1 = 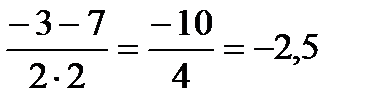 ; х2 =
; х2 = 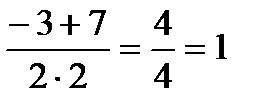 ;
;
+ – +
•//////////•х
–2, 5 1
общее решение:
–2, 5– 1– 0, 5 1
•/////////////o/////////////o/////////• х
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
////////////////////////
х 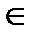 (–0, 5; 1].
(–0, 5; 1].
З а д а н и е 3. Решите систему уравнений:
1) 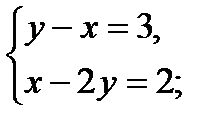 + 2)
+ 2) 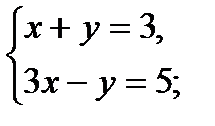 (Д/З)
(Д/З)
– у = 5, – 5 – х = 3,
у = – 5; – х = 3 + 5,
– х = 8,
х = – 8.
Ответ: (– 8; –5).
3) 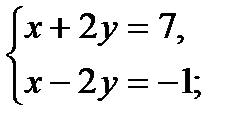

 4)
4)  (Д/З)
(Д/З)
Ответ: (3; 2).
5) 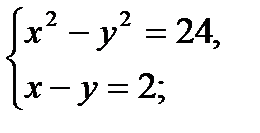
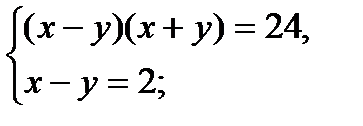

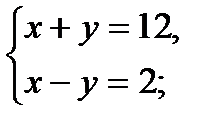

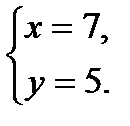
Ответ: (7; 5).
6) 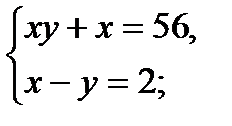
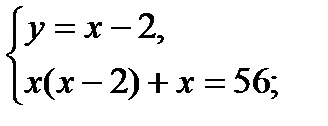
х2 – 2х + х – 56 = 0;
х2 – х – 56 = 0;
по теореме Виета 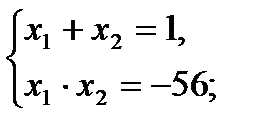
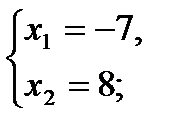
у1 =–7 – 2 =–9; у2 =8 – 2 =6.
Ответ: (–7; –9) и (8; 6).
7) 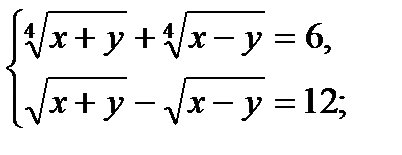 Пусть
Пусть 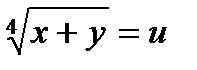 ,
, 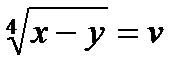 и
и 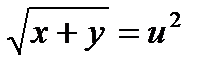 ;
;  , то получим
, то получим
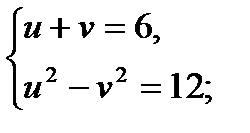
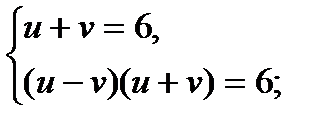
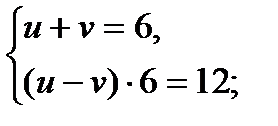
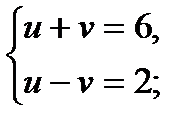
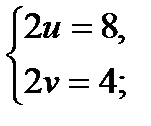
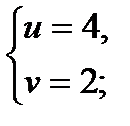
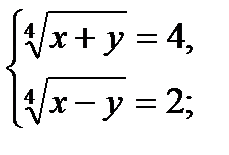
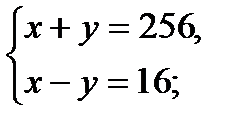
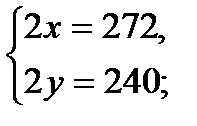
 Ответ: (136; 120).
Ответ: (136; 120).
8)  (Д/З) 9)
(Д/З) 9) 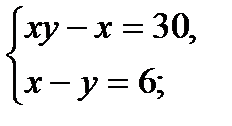 (Д/З) 10)
(Д/З) 10) 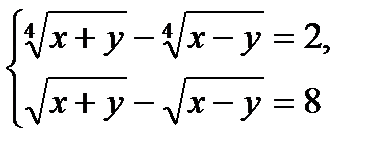 (Д/З)
(Д/З)
11) 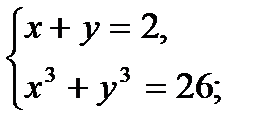

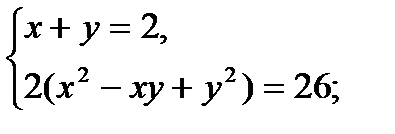
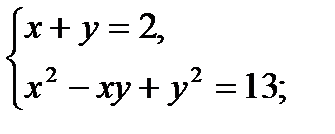
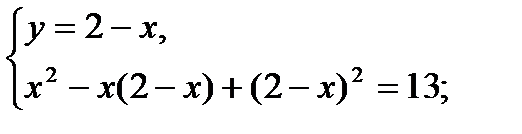
…Дорешать самостоятельно
12) 
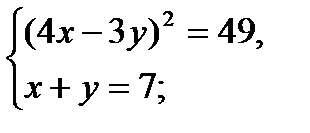
Т. к. уравнение (4х – 3у)2 = 49 можно разбить на два уравнения 4х – 3у = –7 и 4х – 3у = 7, то получим две системы уравнений:
1) 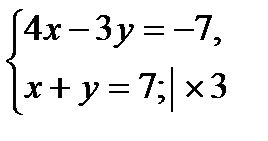 2)
2) 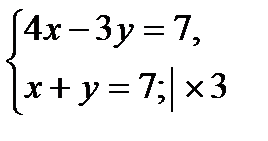

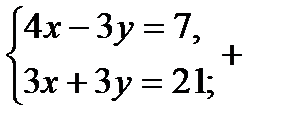
7х = 14; 7х = 28;
х = 2; х = 4;
2 + у = 7; 4 + у = 7;
у = 5; у = 3.
Ответ: (2; 5) и (4; 3)
13) 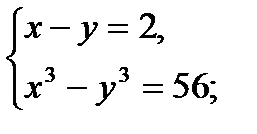 (Д/З) 14)
(Д/З) 14) 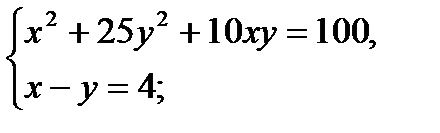 (Д/З)
(Д/З)
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|