Электронная форма.. Бумажная форма.. С-З ЗМШ, 2018 г.. Вступительная работа для 8–11 кл.. Внимание! Для тех, кто с 1 сентября 2018 года будет учиться. в 11 классе – задачи №№ 7–10.

Электронная форма.

Вы изучаете учебные материалы на обучающем сайте; скачиваете оттуда задания; работу выполняете в электронном виде (документ WORD или скан-копия рукописной работы); для проверки загружаете работу на сайт.

Бумажная форма.

Вы получаете учебные материалы и задания обычной почтой в виде брошюр. Работу можно выполнять в тетради, и отправлять на проверку обычной почтой, а можно – в электронном виде и отправлять электронной почтой.

При обеих формах Вы получаете электронной почтой рецензию на вашу работу с разбором ошибок и оценкой.

С-З ЗМШ, 2018 г.

Вступительная работа для 8–11 кл.

Внимание! Для тех, кто с 1 сентября 2018 года будет учиться

в 8 классе – задачи №№ 1–3,

в 9 классе – задачи №№ 3–6,

в 10 классе – задачи №№ 6–9,

в 11 классе – задачи №№ 7–10.

1. В коробке лежат воздушные шарики: 10 красных и 10 синих. Продавец не глядя достает по одному шарику. Сколько шариков ему надо вытащить, чтобы среди них обязательно нашлись: а) два шарика одного цвета; б) два шарика разного цвета; в) три шарика одного цвета?

2. Припишите к числу 10 справа и слева по одной цифре так, чтобы полученное число делилось на 12. Выпишите все такие числа.

3. а) Можно ли занумеровать ребра куба натуральными числами от 1 до 12 так, чтобы для каждой вершины куба сумма номеров ребер, которые в ней сходятся, была одинаковой? б) Аналогичный вопрос, если расставить по ребрам куба числа .

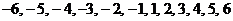4. В равнобедренном треугольнике биссектриса угла при основании равна одной из сторон. Определите углы треугольника.

5. Два города A и B расположены на берегу реки на расстоянии 10 км друг от друга. Пароход может может проплыть из A в B и обратно за 1 час. Больше или меньше времени понадобится ему, чтобы проплыть 20 км по озеру?

6. Найдите целые числа x и y такие, что 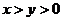и .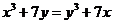

7. Известно, что 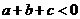и что уравнение 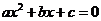не имеет корней. Определите, какой знак имеет число c.

8. Можно ли восстановить треугольник по серединам его сторон? А четырехугольник? Любой ответ требует доказательства!

9. Разложите на множители с целыми коэффициентами:

а) 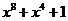(на 3 множителя);

б) 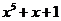(на 2 множителя).

10. а) Докажите, что если 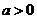, то 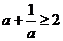. б) Постройте график функции .

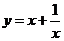Имейте в виду

– Важен не только правильный ответ. Нужно полное решение со всеми выкладками и рассуждениями.

– Не обязательно решить все задачи вашего класса. Сколько сумели решить, столько и запишите.

Желаем успеха!

⇐ Предыдущая 1 23