
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическое занятие. Действия над векторами, заданными своими координатами.
Практическое занятие
Применение векторов и метода координат К решениЮ геометрических задач
Цель практического занятия:
приобрести навыки выполнения действий над векторами;
научиться применять векторы и метод координат к решению геометрических задач.
1. Краткие сведения из теории
Понятие вектора. Некоторые физические величины (сила, скорость, ускорение и др. ) характеризуются не только числовым значением, но и направлением. Такие величины принято изображать направленными отрезками, которые называются векторами.
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор.
Абсолютная величина вектора 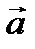 равна квадратному корню из суммы квадратов его координат:
равна квадратному корню из суммы квадратов его координат: 
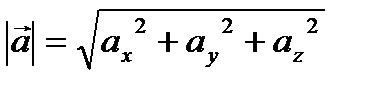 .
.
Действия над векторами, заданными своими координатами.
- При сложении двух (или большего числа) векторов их соответственные координаты складываются:
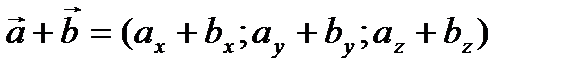 .
.
- При вычитании векторов их соответственные координаты вычитаются:
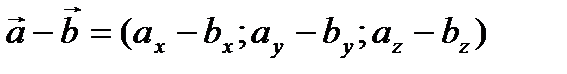
- При умножении вектора на число все его координаты умножаются на это число:
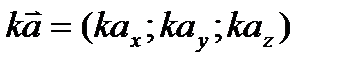 .
.
Пример 1: Даны два вектора 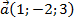 и
и 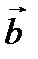 (1; 3; 0).
(1; 3; 0).
1. Найдите координаты векторов 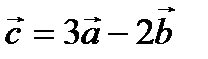 и
и 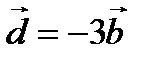 ;
;
Координаты векторов 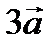 и
и 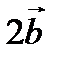 находим по правилу умножения вектора на число: 3
находим по правилу умножения вектора на число: 3 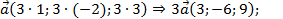
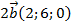 .
.
Координаты вектора 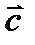 находятся по правилу вычитания векторов:
находятся по правилу вычитания векторов: 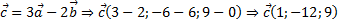
Координаты вектора: 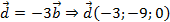
2. Найдите длину векторов 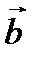 и
и 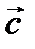 ;
;
Длина вектора 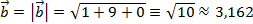 ;
;
Длина вектора 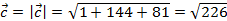 .
.

.
2. Выполните задания в соответствии с номером варианта:
| Даны координаты вершин треугольника ABC. 1. Найдите координаты вектора | ||
| № варианта | Координаты вершин треугольника ABC | |
| A (4; 6; 3), B (-5; 2; 6), C (4; -4; -3).
| |
| 2. 10. 18. | A (4; 3; -2), B (-3; -1; 4), C (2; 2; 1).
| |
| 3. 11. 19. | A (-2; -2; 4), B (1; 3; -2), C (1; 4; 2).
| |
| 4. 12. 20. | A (2; 4; 3), B (3; 1; -4), C (-1; 2; 2).
| |
| 5. 13. 21. | A (2; 4; 5), B (1; -2; 3), C (-1; -2; 4).
| |
| 6. 14. 22. | A (-1; -2; 4), B (-1; 3; 5), C (1; 4; 2).
| |
| 7. 15. 23. | A (1; 3; 2), B (-2; 4; -1), C (1; 3; -2).
| |
| 8. 16. 24. | A (2; -4; 3), B (-3; -2; 4), C (0; 0; -2).
| |
3. Решение типовых примеров:
Даны вершины 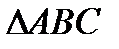 : A (-2; 5; 2), B (2; 3; -1), C (6; 4; -3).
: A (-2; 5; 2), B (2; 3; -1), C (6; 4; -3).
Найдём координаты вектора 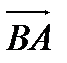 :
:
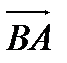 = (
= ( 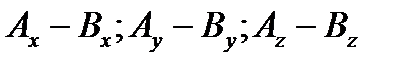 )
)
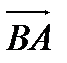 = (-2-2; 5-3; 2-(-1)) = (-4; 2; 3)
= (-2-2; 5-3; 2-(-1)) = (-4; 2; 3)
Аналогично находим координаты вектора 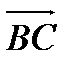 :
:
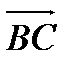 = (6-2; 4-3; -3-(-1)) = (4; 1; -2)
= (6-2; 4-3; -3-(-1)) = (4; 1; -2)
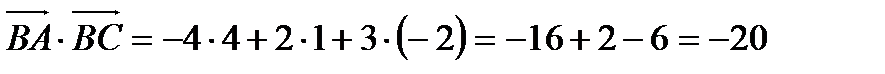
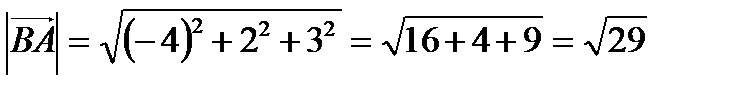
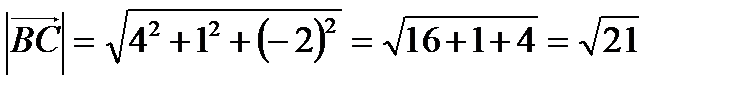
2) Вычислить координаты вектора 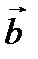 =2
=2 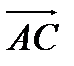 - 4
- 4 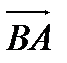 + 3
+ 3 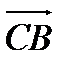
2 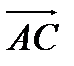 = 2 (8; -1; -5) = (16; -2; -10)
= 2 (8; -1; -5) = (16; -2; -10)
-4 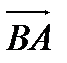 = -4 (-4; 2; 3) = (16; -8; -12)
= -4 (-4; 2; 3) = (16; -8; -12)
3 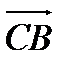 = -3
= -3 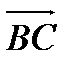 = -3 (4; 1; -2) = (-12; -3; 6)
= -3 (4; 1; -2) = (-12; -3; 6)
2 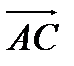 = (16; -2; -10)
= (16; -2; -10)
-4 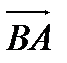 = (16; -8; -12)
= (16; -8; -12)
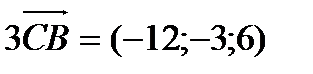
2 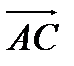 -4
-4 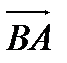 +3
+3 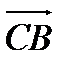 = (20; -13; -16)
= (20; -13; -16)
Ответ: 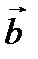 (20; -13; -16)
(20; -13; -16)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
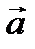 =2
=2 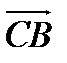 +
+ 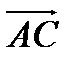 -3
-3 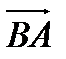 .
.